基于隨機森林的點蝕電位預測

邢易　李樹枝

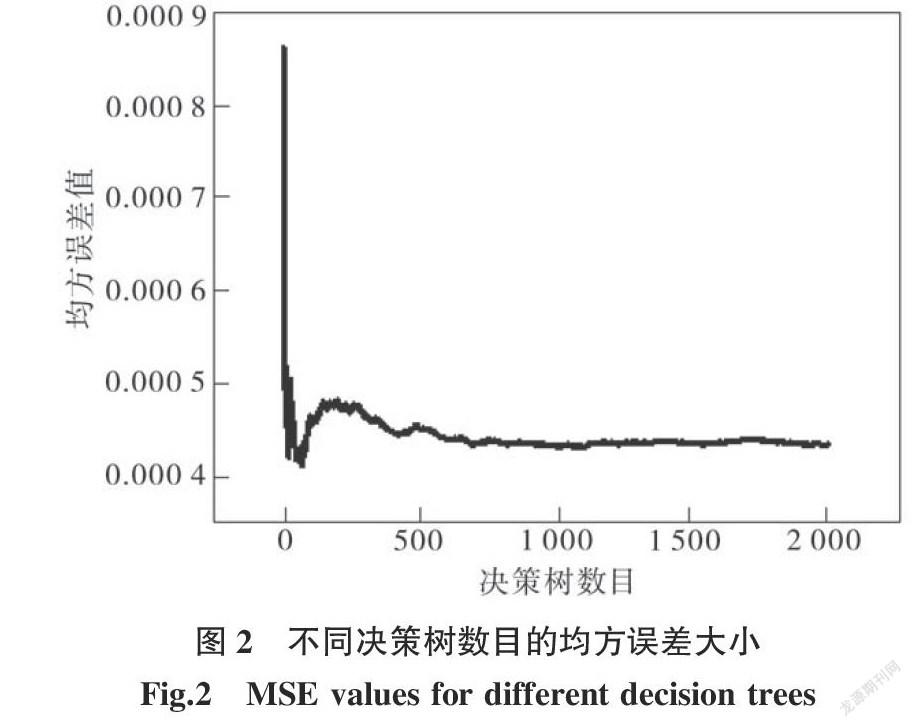
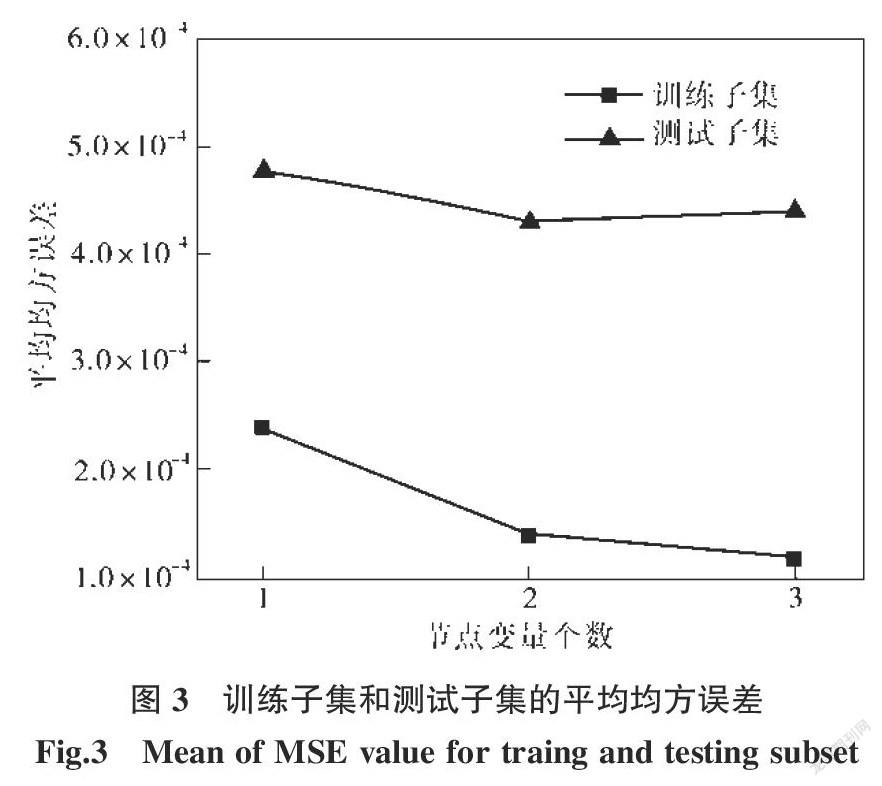
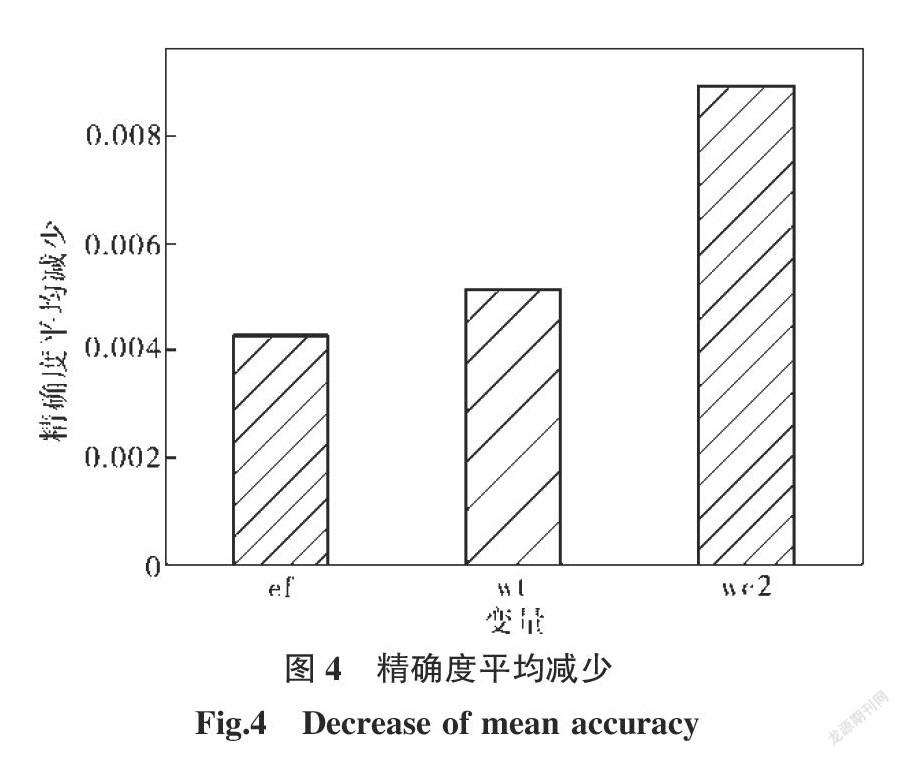
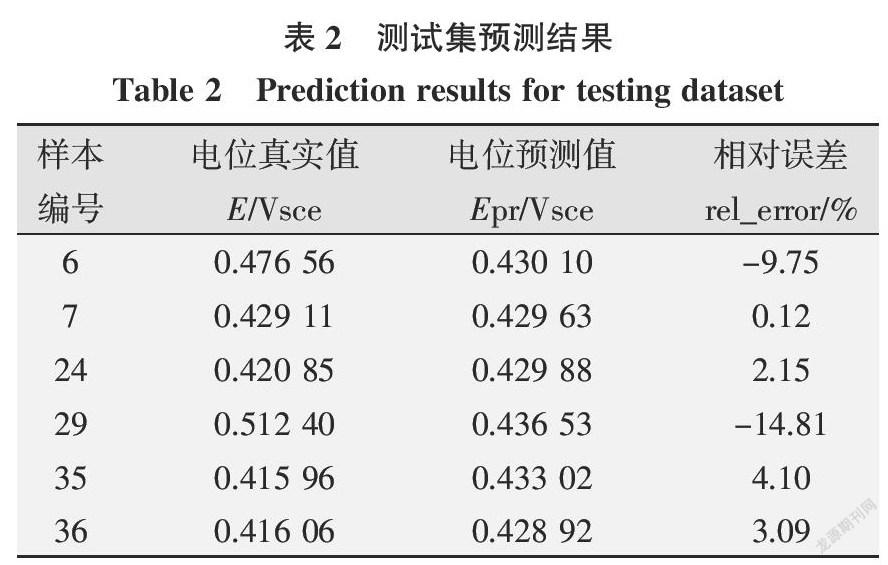
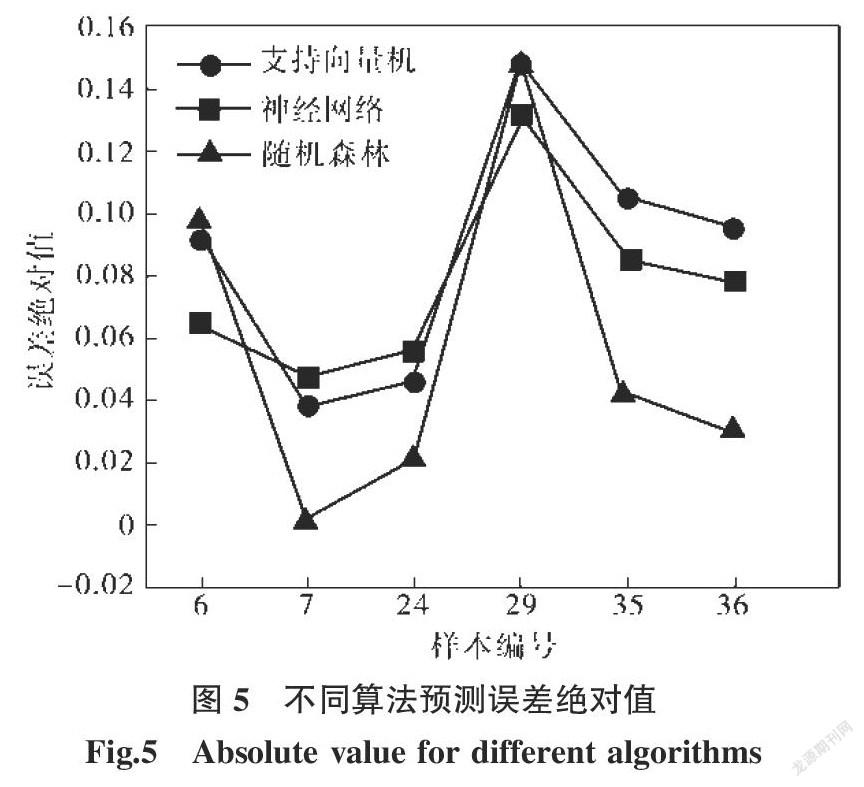
摘要：點蝕是不銹鋼點焊接頭最常見的失效形式之一。點蝕電位作為衡量點蝕行為的特征量，與焊接電流、焊接時間、電極壓力等參數有著復雜的非線性關系。針對文獻中不銹鋼接頭點蝕行為數據，建立隨機森林模型，優化的決策樹數目為1 000，通過“五折交叉驗證”確定節點備選變量個數為2。預測結果表明：除29號樣本預測相對誤差較高外（-14.81%），剩余樣本的預測結果均優于神經網絡和支持向量機，相對誤差的絕對值在10%以下。

關鍵詞：點蝕電位;隨機森林;交叉驗證;非線性

中圖分類號：TP181文獻標志碼：A文章編號：1001-2303（2020）05-0045-05

DOI：10.7512/j.issn.1001-2303.2020.05.09

0 前言

電阻點焊以其高效、低應力、小變形以及良好的自動化適應性等優勢，廣泛應用于汽車、鐵路、航空、電子等工業領域中，可實現低碳鋼、不銹鋼、鋁合金、高溫合金的焊接。

不銹鋼具有優良的機械性能和耐蝕性能，但在點焊過程中其接頭性能受到較大影響，尤其是耐蝕性。點蝕是一種局部腐蝕現象，點蝕電位作為點焊接頭點蝕行為的評價依據，可通過焊接時間、焊接電流等[1-3]焊接參數實現預測和評價。

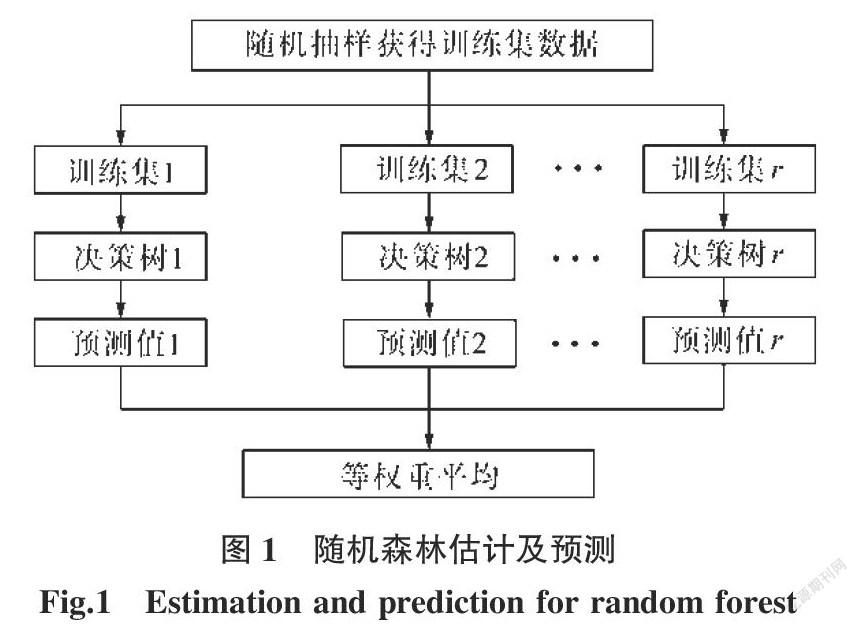
隨機森林是Breiman L.[4]在2001年提出的機器學習算法。該算法以決策樹作為基學習器，采用并行化思想，實現模型的訓練和預測。隨機森林算法優點眾多，非常適用于處理復雜、非線性問題，而且幾乎不會出現過擬合，預測效果好，在農業、林業、生物醫藥、信息通訊等[5-9]眾多領域中有著重要應用。李欣海[5]利用隨機森林對昆蟲種類進行判別;陳華舟[6]將隨機森林回歸與基尼系數優選變量方法結合，實現魚粉蛋白的定量分析預測;Milad Malekipi-rbazari[9]利用隨機森林模型進行社交借貸風險評估。……