C藤Copula自回歸模型及其預測
王羅楠,李述山
(山東科技大學 數學與系統科學學院,山東 青島 266000)
在金融時間序列分析領域,經典的ARMA類模型是目前最常用的平穩時間序列擬合模型,但這類模型本質上是線性模型,不但不能刻畫金融時間序列中的非線性相關信息,而且無法解釋金融時間序列呈現出的波動聚集、尖峰厚尾等時變特征。Engle[1]提出ARCH模型,將歷史波動信息作為條件,采用自回歸的形式來刻畫波動的變化,克服了ARMA類模型的局限性。隨后,Bollerslev提出GARCH模型,克服了ARCH模型滯后階數過大的缺點[2]。GARCH模型能夠迅速捕獲聚集性波動,反映金融時間序列中所蘊含的風險,但這類模型同樣也無法充分利用金融時間序列中的非線性相關關系。
Copula函數是一類定義在[0,1]上的多維聯合分布函數,它能夠將多個隨機變量的邊際分布連接起來得到它們的聯合分布,在金融市場間相關性分析、金融風險管理等方面有著廣泛的應用。為解決傳統Copula模型難以擴展到高維的問題,Joe等[3]在多元Copula的基礎上發展了Pair-Copula,將高維隨機變量的聯合分布分解為一系列邊緣分布和Pair-Copula函數的乘積。隨后,Tim等[4]基于Pair-Copula理論提出了藤Copula模型,運用圖論的方法詳細描述了各變量間的連接關系,為構建高維隨機變量聯合分布函數提供了一種簡便清晰的方法。C藤Copula模型是藤Copula模型中應用最為廣泛的模型之一,適合描述具有根節點變量的多個變量之間的相關關系。在以往的大部分文獻中,Copula函數和藤Copula模型往往被應用于研究多個時間序列之間的相依性[5-6],本文將Copula函數和C藤Copula模型運用于研究嚴平穩時間序列的非線性自相關性,建立C藤Copula自回歸模型,提取序列中有用的信息,并運用模型進行預測。
本文的主要工作是:(1)研究嚴平穩時間序列的非線性自相關性,建立C藤Copula自回歸模型,給出序列相關自變量的篩選方法;(2)給出C藤Copula自回歸模型的參數估計方法和預測方法;(3)運用模型進行預測和對比分析,通過實例來說明模型的有效性和實用價值。
1 C藤Copula自回歸模型
1.1 C藤Copula模型
考慮n維隨機變量(X1,X2,…,Xn),設其聯合分布函數和聯合密度函數分別為F(x1,x2,…,xn)、f(x1,x2,…,xn),邊際分布函數和邊際密度函數分別為Fi(xi)(i=1,…,n)、fi(xi)(i=1,…,n)。C藤結構的每棵樹Tj有且僅有一個節點連接到n-j條邊,這個節點被稱為根節點,每條邊對應一個Pair-Copula。n維隨機變量的C藤Copula密度函數可以表示為[7]
(F(xj|x1,…,xj-1),F(xj+i|x1,…,xj-1))
(1)
式中:j為第j棵樹Tj的標號;i遍歷所有樹的每一條邊。
本文運用C藤Copula模型研究嚴平穩時間序列的非線性自相關性,找出序列中與t時刻條件分布相關的連續滯后項個數,以這些滯后項為自變量建立C藤Copula自回歸模型,從而剔除與t時刻不相關的歷史信息,更加充分地利用序列的非線性自相關性。
1.2 C藤Copula自回歸模型
設{Xt}為一嚴平穩時間序列,若在t時刻xt的條件分布僅與其前k個滯后項xt-1,xt-2,…,xt-k有關,而與其他滯后項xt-k+1,xt-k,…無關,那么剔除與xt不相關的歷史信息,建立以xt-1,xt-2,…,xt-k為自變量,xt為因變量的自回歸模型,就能夠充分利用t時刻之前的歷史相關信息,完成對xt的預測。因此本文將結合C藤結構的思想,建立C藤Copula自回歸模型,利用xt的前k個滯后項xt-1,xt-2,…,xt-k,預測t時刻的值xt。
為方便描述,本文將xt節點記為k+1,將其前k個滯后項節點xt-1,xt-2,…,xt-k記為1,2,…,k,作出C藤Copula自相關模型的結構圖,如圖1所示。
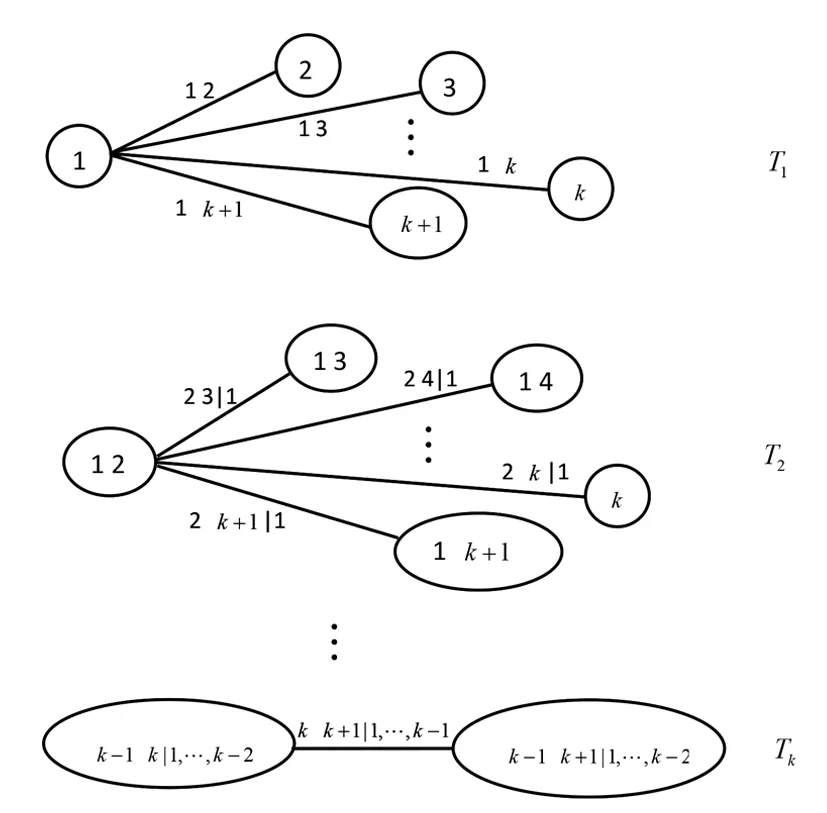
圖1 C藤Copula自相關模型結構圖Fig.1 Structural chart of the C-Vine Copula autoregressive model
由圖1和式(1)得出,條件集為xt-1,xt-2,…,xt-k時,xt的條件密度為
F(xt|φt-i-1))
(2)
式中:φt={xt-1,xt-2,…,xt-k},表示t時刻前1階到前k階滯后項的集合;φt-i={xt-i,xt-i-1,…,xt-k},(1 設與xt相關的連續滯后項個數為k,那么自變量集合為φt={xt-1,xt-2,…,xt-k},結合條件密度函數表達式(2)建立C藤Copula自回歸模型: (3) 其回歸函數為 (4) 考慮嚴平穩時間序列{Xt},若存在任一k(k∈N+)滿足:對于任意q∈N+,在條件集(Xt-1,Xt-2,…,Xt-k)已知時,Xt與Xt-k-q條件獨立;在條件集(Xt-1,Xt-2,…,Xt-k+1)已知時,Xt與Xt-k不條件獨立,則稱Xt-1,Xt-2,…,Xt-k為序列{Xt}在t時刻的k個相關自變量。 (5) H00:對于任意q∈N+,Hk,1|Φt(Xt|Φt)與Hq,k|Φt(Xt|Φt)獨立; 本文采用兩步法對模型參數進行估計。第一步估計邊際分布參數,第二步估計相關Copula參數。 邊際分布有多種擬合方法,由于帶位置參數與尺度參數的有偏廣義誤差分布(SGED)能夠很好地刻畫收益率序列尖峰后尾的特征,因此本文選取此分布來擬合收益率序列的邊際分布。將得出的邊際分布函數帶入C藤Copula的對數似然函數,便可以對相關Copula參數進行極大似然估計,其中C藤Copula的對數似然函數為[9] …,xt-i+1),F(xt-i-j|xt-1,…,xt-i+1) (6) 式中:θ為Copula參數的集合;T代表觀察值的組數。 在實證分析中,為了保證估計精度,本文模型中所涉及的Copula及Pair-Copula均采用混合Copula。由n個不同種類Copula函數得到的混合Copula函數表達式為 MCn=ω1C1(θ1)+ω2C2(θ2)+ …+ωnCn(θn) (7) 式中:ω1,ω2,…,ωn表示n個不同Copula函數相應的權重系數,ω1,ω2,…,ωn≥0,ω1+ω2+…+ωn=1;θ1,θ2,…,θn為相應的相關系數。 (8) [qα/2,q1-α/2] (9) 本文選取近20年共5 081個深證成指每日收盤數據作為樣本觀察值,數據涵蓋1998年1月5日至2018年12月19日,并使用日對數收益率xt=lnpt-lnpt-1(t=1,2,…,5 081)作為研究指標,其中pt表示第t日收盤價。借助Matlab進行數據建模與分析,得到對數收益率序列的描述性統計及ADF檢驗結果,見表1。 表1 描述性統計及ADF檢驗結果Tab.1 Descriptive statistics and ADF test results 由表1可知xt序列偏度為負值,峰度為6.518 7,因此序列為有偏的,且表現出顯著的尖峰厚尾特征。ADF檢驗統計量的值為-67.480 1,對應P值接近0,在0.01的顯著性水平下拒絕原假設,表明對數收益率序列為平穩序列。 3.2.1 邊際分布 鑒于xt為有偏的、具有顯著尖峰厚尾特征的序列,因此本文采用有偏廣義誤差分布(sged)擬合序列的邊際分布,并通過K-S檢驗進行擬合優度評估。得出邊際分布參數的最大似然估計值及K-S檢驗結果,見表2。 表2 邊際分布參數估計及K-S檢驗結果Tab.2 Parameter estimation of marginal distribution and K-S test results 其中μ、σ、k、λ分別為有偏廣義誤差分布的位置參數、尺度參數、分布參數和偏度系數。表中K-S檢驗的H值為0,并且K-S統計量及其概率值表明,沒有充分的理由拒絕“xt的邊際分布符合有偏廣義誤差分布”的原假設。 3.2.2 Copula函數參數估計 本文采用混合Copula對所涉及的Copula及Pair-Copula函數進行擬合。由于雙參數的BB1 Copula函數能夠較好地描述非對稱的上下尾相依性,同時本文所涉及的變量間具有較弱的非線性相關性和較強的獨立性,而獨立Copula能夠較好地刻畫這種獨立性,故本文選用BB1 Copula和獨立Copula[10]的混合Copula對所涉及的Copula及Pair-Copula函數進行擬合。 根據圖1依次畫出k=1,…,i(i∈N+)時收益率序列的自相關結構圖,結合本文給出的參數估計和假設檢驗方法分別對所求出的條件分布函數進行水平為0.05的獨立性檢驗,在k=5時接受原假設H00和H10,確定對數收益率序列xt在t時刻相關自變量的個數為5,故建立5階C藤Copula自回歸模型。 假設檢驗及模型建立過程中所涉及的Copula和Pair-Copula參數估計結果見表3和表4,其中獨立Copula和BB1 Copula的權重ω1、ω2以及BB1 Copula的參數θ、δ通過EM算法[11]進行估計。 表3 Copula參數估計結果 Tab.3 Copula parameter estimation results 表4 Pair-Copula參數估計結果 Tab.4 Pair-Copula parameter estimation results 3.2.3 模型預測 通過建立5階C藤Copula自回歸模型,本文可以對收益率序列時刻6及其以后的點進行預測。運用本文給出的預測方法,作出收益率序列最后1 000個真實值與C藤Copula自回歸模型預測值對比效果圖,如圖2所示,收益率序列的最后1 000個真實值與C藤Copula自回歸模型置信度為95%的置信區間對比如圖3所示。可以看出,預測值與置信區間具有顯著的時變特征,實際值趨于密集時預測值相對密集,實際值趨于離散時預測值也趨于離散,置信區間將大部分真實值包含在內。 圖2 真實值與預測值對比圖Fig.2 Contrast chart between real value and predicted value 圖3 真實值與95%置信區間對比圖Fig.3 Comparison between true value and 95% confidence interval 為了顯示C藤Copula自回歸模型的預測效果,本文將5階C藤Copula自回歸模型的預測結果分別與ARMA(1,1)模型和Garch(1,1)模型進行對比,結果見表5和表6。由表5可知,從平均絕對誤差的角度來看,5階C藤Copula自回歸模型的預測效果優于ARMA(1,1)模型,與Garch(1,1)模型的預測效果相當,但最大絕對誤差相對較小,因此總體上可以認為5階C藤Copula自回歸模型的預測效果優于ARMA(1,1)模型和Garch(1,1)模型。由表6可知,在95%置信水平下,5階C藤Copula模型的置信區間所包含的真實值百分比最大,并且非常接近置信水平,因此從置信區間角度來看,5階C藤Copula模型的預測效果同樣優于ARMA(1,1)模型和Garch(1,1)模型。 表5 預測結果對比表 Tab.5 Comparison table of prediction results 表6 95%置信水平下置信區間對比表Tab.6 Confidence interval contrast table under 95% confidence level 1)通過運用C藤Copula理論,建立了C藤Copula自回歸模型,給出了嚴平穩時間序列某一時刻相關自變量個數的確定方法,從而剔除了不必要的歷史信息,提高了預測精度。 2)基于C藤Copula自回歸模型對深證成指5 081個日收益率數據進行了實證分析,并將預測結果與ARMA(1,1)模型和Garch(1,1)模型做比較,結果顯示預測效果優于ARMA(1,1)模型和Garch(1,1)模型,從而證明了模型的可行性和實用價值。 3)本文的研究方法還有待改進。在實際操作方面,邊際分布有多種擬合方式,可以選擇不同的擬合方式比較擇優,此外,對混合Copula估計可以引入更多的Copula函數;在實際應用方面,C藤Copula自回歸模型還可以運用于風險價值分析,如VaR、CVaR估計等。1.3 相關自變量篩選方法
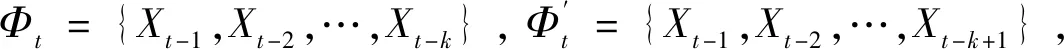
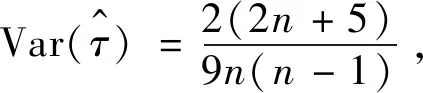
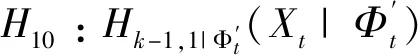
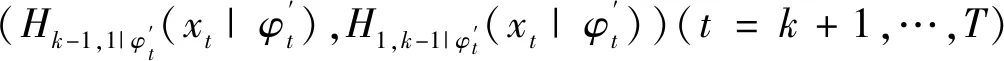
2 參數估計及預測
2.1 模型參數估計
2.2 模型預測方法
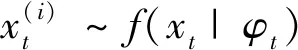
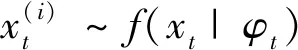
3 實證分析
3.1 數據的描述性統計及平穩性檢驗

3.2 模型建立

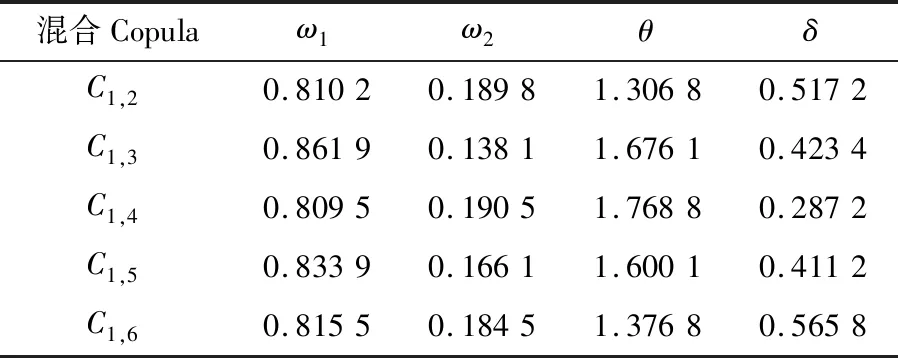

4 結束語

