考慮土拱效應的盾構隧道施工地表沉降規律研究

黎春林

(銅陵學院 建筑工程學院，安徽 銅陵 244000)

隧道施工時易因地層損失引起隧道拱頂沉降，并由拱頂逐漸向地表進行傳遞。PECK公式因其簡單實用，目前在地下工程施工地面沉降的結算中得到廣泛應用。PECK公式的核心在于假定地表沉降符合正態分布規律，并認為地表沉降槽面積等于地層損失[1]。這雖然簡化了分析，但忽略了土體在開挖前后應力狀態的變化而產生的變形，必然帶來誤差。實際上，在土體變形由拱頂向上傳遞的過程中，因土拱效應[2]，部分土體自重應力被轉移到鄰近土體，引起隧道拱頂土體回彈變形，因此土體沉降槽面積是小于地層損失的，這部分變形不可忽視，這也使得在實際工程中PECK公式計算的沉降值偏大。本文在PECK公式基礎上進一步討論考慮土拱的卸載效應后隧道上覆土層豎向位移的計算方法。

1 隧道拱頂沉降計算理論

1.1 地表沉降

Lo等[3]、Rowe等[4]提出等效地層損失概念，認為拱頂最大沉降量為：

Smax=ga

(1)

式中，ga表示地層損失參數，采用公式(2)計算：

ga=(1-m)(Gp+U3D+ω)

(2)

式中：m表示注漿充填率，Gp為地層損失，也即盾尾空隙，U3D為因施工擾動引起土體變形而擠入隧道凈空而被開挖引起的地層損失，ω為施工因素引起的地層損失。Lee等[5]給出了以上各參數的計算方法，這里不再贅述。

PECK公式假定地表沉降曲線符合正態分布，則

(3)

式中：Smax(0)為隧道軸線處地表最大沉降，S(x)為距離隧道軸線水平距離為x的地表沉降，i(0)為地表沉降槽寬度系數，也即圖1中反彎點到隧道軸線的水平距離。

(4)

式中，φ為土體內摩擦角，Z0為隧道中心深度。由式(3)繪制的地面沉降分布曲線如圖1所示。

圖1 地表沉降計算示意圖Fig.1 The schematic drawing for calculation of ground surface settlement

如果假定沉降槽面積等于地層損失，則

(5)

也即

(6)

1.2 任意深度土體沉降

PECK公式假定地表沉降槽面積與地層損失相等。為簡化分析，許多學者[6-7]沿用這一假定，認為在地面以下隧道拱頂土層任意深度處沉降槽面積依然等于地層損失，由此可進一步建立任意深度z處隧道施工引起的地層損失量Vs(z)與埋深為z處的地層最大位移Smax(z)之間的關系為：

2.5i(z)·Smax(z)

(7)

也即

(8)

式中：z為土層埋深；Smax(z)為埋深z處的隧道中心拱頂最大位移；i(z)為埋深z處的沉降槽寬度系數；i(z)=Kz(Z0-Z)；式中Kz為深度為Z處的系數，其計算方法很多，詳見文獻[8]。

實際上，式(5)和式(7)假定沉降槽面積與地層損失相等與工程實際是不相符的。因為施工擾動，隧道上方土層應力重分布，部分豎向應力會通過剪應力向臨近的土體進行轉移，也即存在土拱效應。對于淺埋隧道的土拱發展對拱頂松動土壓力影響在文獻[9]中有詳細討論。

土拱的發展使得隧道上方土體中一部分應力釋放，因此土體會出現回彈，故地層中沉降槽的面積應該是小于地層損失的；而且越靠近地表，沉降槽的面積與地層損失的差值越大。

PECK公式假定沉降槽的面積與地層損失相等，會使得預測的沉降結果偏大，這也在工程實際中得到了大量的驗證。文獻[10]通過對廣州地鐵施工現場的實測數據進行了大量的統計分析，認為需要對PECK公式計算的沉降值進行修正，在對比分析的基礎上，他認為PECK公式計算的最大沉降值需乘以一個折減系數α，α的大小在0.5～1.0之間；譚文輝等[11]通過對北京地鐵 7 號線現場施工引起的地表沉降的現場測量，并將實測數據和 PECK 公式進行了對比分析，也認為應該對地表最大沉降量進行修正，并認為修正系數α介于0.613～0.620之間。文獻[12]根據蘇州地鐵盾構施工現場地表沉降實測數據，發現現場沉降實測值小于PECK公式理論值，論文通過調整沉降槽寬度系數與地層損失率，對 PECK公式進行修正。文獻[13]根據與地表沉降實測數據的比較，也發現現場沉降實測值小于PECK公式理論值。以上這些文獻沒有從理論上分析原因，對PECK公式所作的修正都只適用于特定的土質條件和施工條件、特定的隧道直徑及隧道埋深，沒有普適性。

基于此，本文從土拱效應引起拱頂土體卸荷、土體回彈變形的角度來具體分析PECK公式理論計算值偏大的原因。

2 考慮土體回彈變形的沉降計算方法

考慮土體回彈后，在隧道上方任意深度z處的沉降槽面積Vs(z)修正為：

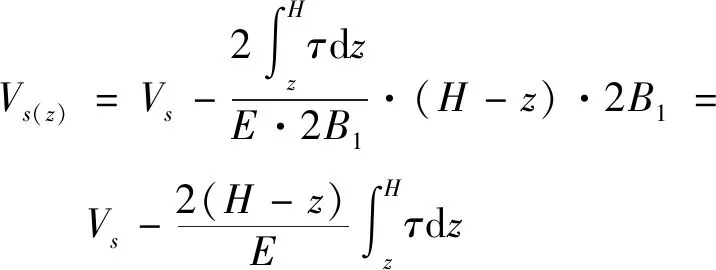
(9)

圖2 隧道拱頂滑動柱示意圖Fig.2 The schematic drawing of the sliding surface on vault of tunnel

圖2中，土體實際滑動面為aa，為簡化分析，假定滑動面為ab，滑動土柱寬度為2B1。

特別地，對于地表(z=0)的沉降槽面積為：

(10)

將式(10)代入式(6)中，可求得地表最大沉降Smax：

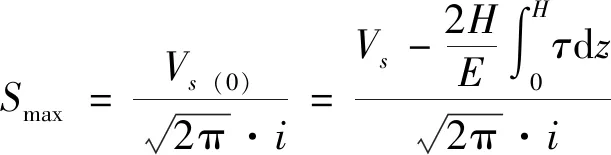
(11)

將式(4)代入式(11)中，可進一步求得：

(12)

3 土拱效應下土中地層損失簡化分析

土體實際滑動面為圖2中aa，為簡化分析，假定滑動面為圖2中ab，據此建立下面的簡化計算模型，如圖3所示。

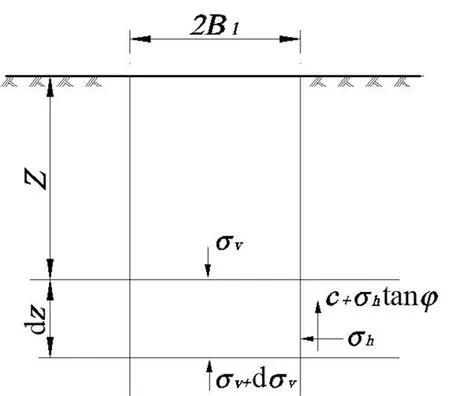
圖3 剪應力簡化計算模型Fig.3 Simplified calculation model for the shearing stress

如圖3所示，當土拱效應充分發揮、土體瀕臨破壞時，滑動面上的剪應力等于抗剪強度，即土中剪應力τmax=τf=c+σhtanφ。在土中取一微單元，作用在微單元上的剪應力合力dq為：

dq=2cdz+2σhdztanφ=2cdz+2Kσvdztanφ=2cdz+2Kγzdztanφ

(13)

式中K為側壓力系數，這里取主動土壓力系數，即K=tan2(45°-φ/2)。

由公式(13)可以計算出當土拱效應充分發揮時，作用在每一個土體微單元上的剪應力合力dq，該剪應力合力和土體重力的作用力方向相反，使得隧道拱頂土體出現卸荷回彈。

假定隧道拱頂土層厚度為H，則因土拱效應引起的隧道拱頂覆土厚度H內所有土體總卸荷q為：

(14)

考慮土體卸荷回彈后地層損失會減少，沉降也會相應減少，文獻[14]利用1stOpt軟件對ANSYS有限元計算結果使用PECK公式進行回歸分析，得出地表最大沉降量與彈性模量E約為對數關系，但僅僅是通過數理統計得出的結論，沒有揭示兩者的內在關聯。

本文將根據土體的回彈變形建立兩者的解析關系如下。考慮土體卸荷回彈后的地層損失為：

(15)

假定地表沉降橫向分布曲線為正態分布曲線，則地面沉降橫向分布曲線為：

(16)

式(16)與PECK公式相比，考慮了因土拱效應拱頂土體應力轉移引起的土體卸載回彈。

4 本文推薦方法工程應用分析

為了進一步驗證公式(16)的有效性，下面對本文提出的方法、PECK方法和現場實測數據作比較分析。

試驗地段在無錫地鐵1號線南禪寺～永豐路盾構區間，隧道直徑3.1 m，地表覆土厚度9.2 m，隧道軸線埋深12.3 m,隧道拱頂土層的工程地質特征及分布見表1。實驗區間工程地質縱剖面圖如圖4所示。

表1 隧道拱頂土層的工程地質特征及分布Tab.1 Engineering geological characteristics of soil on vault of tunnel

圖4 實驗區間工程地質縱剖面圖Fig.4 Longitudinal profiles of engineering geology in the experimental field

根據現場鉆孔取樣原狀土室內實驗，并對該盾構拱頂土體的物理力學參數根據上覆土層各土層厚度取加權平均，得土的容重為18.9 kN/m3，土的粘聚力c=9.5 kPa，土地內摩擦角φ=22°，土的回彈模量42.5 MPa。

根據現場施工資料，盾構施工控制的地層損失率為1.2%，對應的地層損失為：

則由式(15)得地表地層損失為：

則由式(12)得地表最大沉降為：

則由公式(16)即可繪出地面橫向沉降分布曲線，并和PECK方法計算的地表沉降值及實測值比較，如圖5所示。

圖5 地表沉降計算值與實測值比較Fig.5 Comparison of computational value and experimental value for the surface subsidence

計算結果顯示，本文方法計算得到的地表沉降曲線與實際地表沉降曲線的形狀吻合度較好。與PECK公式比較，因考慮了土體卸荷反彈，本文提出的方法相比PECK方法計算得到的地表沉降要小。特別是當地層損失量較大、土拱效應發揮比較充分的情況下，兩者的差異將更加明顯。而當隧道成拱條件較差時，因土拱效應不能充分發揮，拱頂松動土壓力與原始地應力差值較小，因此土體回彈也很小，此時本文方法和PECK方法結果近似一致。

5 結論

本文在傳統PECK理論公式的基礎上，對隧道施工土體沉降進行了探討。考慮土拱效應的卸荷作用后，拱頂土體沉降槽的面積因為土體卸荷回彈小于地層損失，故越靠近地表，土體沉降槽的面積與地層損失的差值越大，造成PECK公式計算的沉降值越大。特別是當地層損失較大、土體剪應力發揮比較充分時，沉降值偏大。因此，在此類工程情況下，應根據剪應力沿土體深度的分布規律對PECK公式進行修正。