未知不對稱死區補償方法在三軸微機電陀螺控制中的應用

卓書芳，黃宴委，何用輝，郭世南

(1.福建信息職業技術學院 自動化工程系，福建 福州 350003；2.福州大學 電氣工程與自動化學院，福建 福州350116)

MEMS陀螺儀是一種新興的慣性角速率傳感器，以其極小體積質量、極低成本功耗的優點，已在慣性導航、汽車工業、生物科技和消費終端等領域得到大量應用[1-2]。然而，由于微加工帶來的機械耦合、不等彈性、熱力學噪聲、尺度效應、微弱信號檢測等技術約束，大多數商用MEMS陀螺僅限于速率級水平[3]，仍屬于中低精度的慣性器件，因此從不同途徑提高角速率檢測精度成為研究熱點。

在MEMS陀螺的常規操作模式下，要求激勵電壓與驅動模態/敏感模態諧振。顯然，這種一軸驅動一軸檢測的操作模式存在本質缺陷：為削弱驅動模態上的耦合哥氏力，要求敏感模態振幅約為驅動模態的千分之一，這不利于信號檢測[4]。為此，Park 等[5]率先提出一種全新的MEMS陀螺驅動檢測原理，將力反饋控制思想和自適應控制中的持續激勵理論結合應用在MEMS陀螺的雙軸閉環控制中，將陀螺的測量問題轉化為參數估計問題。在Park等操作模式啟發下，James等[6]提出了一種新概念三軸MEMS陀螺結構，該結構理論上用一個振動質量塊即可檢測三個軸向的角速度。在這種新概念三軸陀螺的研究中，Fei等[7]應用神經網絡和模糊邏輯[8]補償系統的參數不確定性和阻尼剛度耦合。而王偉等[9]則關注了力電換能過程中的扇區有界非線性效應，應用自適應控制對扇區下界進行估計補償。本文在上述基礎上，研究力電換能過程中的死區效應，采用兩個耦合 RBF神經網絡分別逼近執行器死區的逆和經過死區后的不可測控制力。穩定性分析中權值矩陣的更新采用弱耦合自適應律實現，利用比例微分滑模面實現陀螺三軸的軌跡跟蹤。

1 三軸MEMS陀螺動力學及死區建模

1.1 三軸MEMS陀螺動力學模型

常規MEMS陀螺的z方向懸空，而文獻[6]所提的新概念結構在z軸方向分別添加驅動和敏感模塊，如圖1所示。

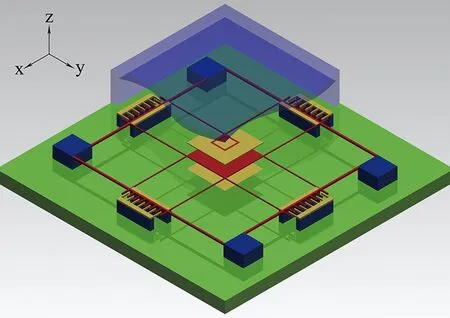
圖1 單質量塊三軸MEMS陀螺儀概念圖Fig.1 Conceptual structure drawing of single-mass MEMS triaxial gyroscope

考慮不理想的陀螺正交耦合，三軸MEMS陀螺的動力學方程可以用如下的二階線性常微分方程組表示:

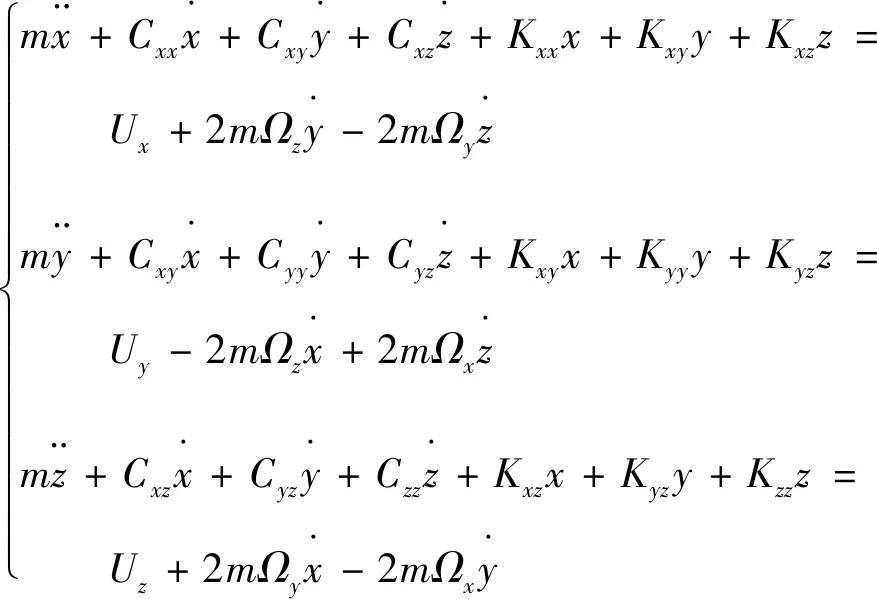
(1)

式中：Ux,Uy,Uz表示三個軸向的再平衡控制；Cxx,Cyy,Czz為三個軸向的等效阻尼項；Kxx,Kyy,Kzz為三個軸向的等效剛度項;假設機械正交耦合導致對稱的阻尼項Cxy,Cxz,Cyz和剛度項Kxy,Kxz,Kyz；Ωx,Ωy,Ωz是三個軸向的外部載體角速度。

參考文獻[10]，對上式的動力學模型進行無量綱化處理，得無量綱化的矩陣系數方程為

(2)

式中

1.2 三軸MEMS陀螺驅動梳齒的死區模型

MEMS陀螺儀三軸的驅動梳齒死區特性如圖2所示。其數學表達式為

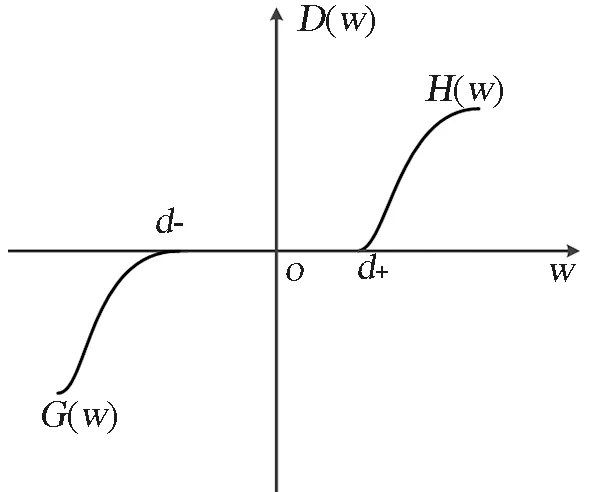
圖2 未知不對稱死區Fig.2 Unknown asymmetric dead zone

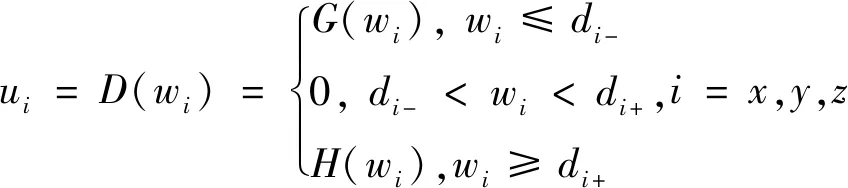
其中：wi為陀螺驅動梳齒的電壓輸入；ui為相應驅動梳齒生成的驅動；H(wi)和G(wi)分別表示正負死區的未知連續特性；di-和di+分別表示死區的負邊界和正邊界。補償思路為死區逆模型串聯理想控制器，其中死區逆模型D-1(wi)利用RBF補償網絡進行局部反饋獲取。死區逆模型假設為

(3)

式中v為理想控制器輸出。從而有

D(D-1(v))=v

(4)

控制的目的是希望驅動梳齒的輸出u近似等于理想控制器輸出v。考慮實際應用，兩個假設如下：

假設1 驅動梳齒的死區輸出u不可測。

假設2 死區參數的真實值H(w),G(w),d-和d+都是未知，H(u)和G(u)在規定區域內為單調可逆增函數，d-<0,d+>0,H(w)>0,G(w)<0。

2 基于自適應神經網絡的三軸MEMS陀螺死區補償設計

神經網絡補償器的基本原理如圖3所示。

圖3 神經網絡補償器原理圖Fig.3 Schematic diagram of neural network compensator

其中,v為理想控制器生成的控制信號,w為死區補償后的實際控制輸入,u為經過驅動梳齒后作用到檢測質量塊的物理控制力。

由圖3可知

(5)

式(5)的死區逆可等效表示為

D-1(v)=v+vNN

(6)

式中

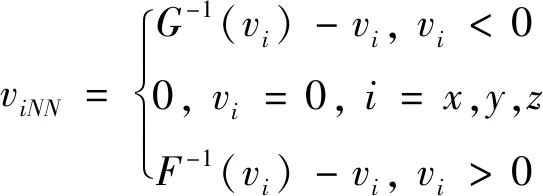
(7)

利用RBF網絡的無限逼近特性可得：

(8)

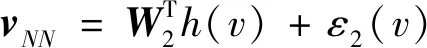
(9)

(10)

式中：w,v分別為兩個神經網絡的輸入信號；j為隱層節點的個數；hj為高斯基函數的輸出；W1,W2分別為補償不確定性和補償死區的理想權值；ε1,ε2為兩個網絡的逼近誤差。根據u,vNN的表達式，兩個RBF神經網絡的輸出可分別表示為：

(11)

(12)

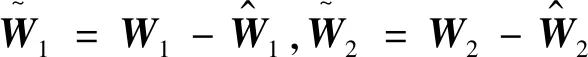
(13)

假設3 兩個權值矩陣范數有界，且滿足‖W1‖F≤γ1,‖W2‖F≤γ2。

假設4 兩個網絡的逼近誤差范數有界，且滿足‖ε1(w)‖≤δ1,‖ε2(v)‖≤δ2。

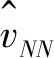
(14)

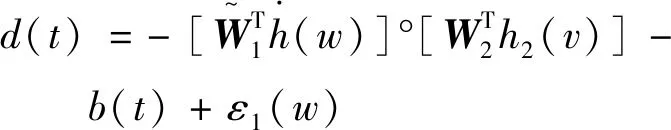
(15)

(16)

式中：L(ξ)為一階泰勒展開的拉格朗日項；符號°表示Hadamard乘積。

證明：

式(5)代入式(8)，得

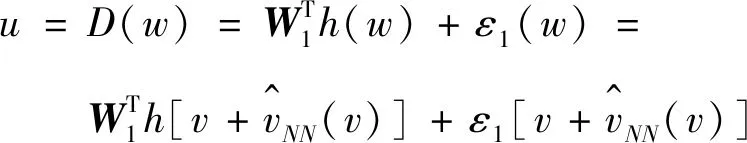
(17)

而根據式(4)和式(6)，得

v=D(D-1(v))=D(v+vNN)

參考式(9)，式(17)為

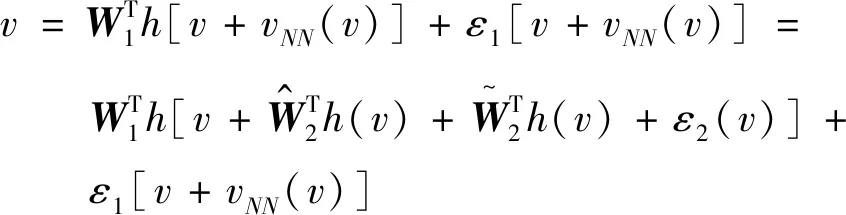
(18)

定義

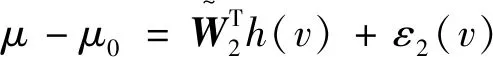
(19)

式中拉格朗日余項為

(20)

將式(19)和式(20)代入式(18)，并將b(t)代入，得

參考式(5)和式(13)，上式為

(21)

式(21)兩邊同時加ε1w并移項整理，得

將式(15)的‖d(t)‖和式(8)代入上式，得

即

d(t)

證畢。

定理2 向量d(t)范數有界，且滿足

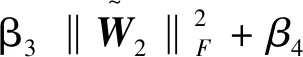
(22)

式中β1—β4均是正常值，其具體表達式如下：

(23)

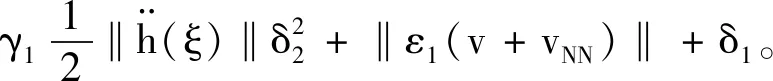
證明：

‖b(t)‖+‖ε1(w)‖

(24)

參考假設3中的‖W1‖F≤γ1,‖W2‖F≤γ2，式(24)為

‖W1‖F‖L(ξ)‖+‖ε1(v+vNN)‖+

‖ε1(w)‖

(25)

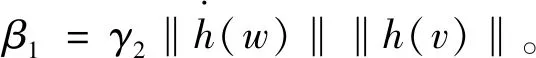
參考式(20)和假設4，式(25)為

證畢。

神經網絡補償器中權值矩陣的傳統自適應律分別設計為：

(26)

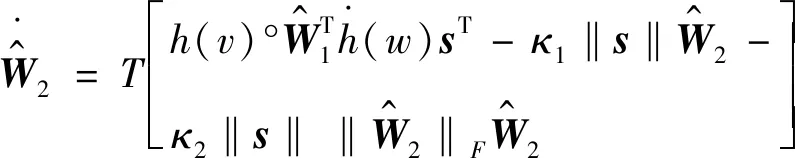
(27)

式中：S,T分別為正定對稱陣，滿足ST=S,TT=T；正常數κ1≥0,κ2≥0；s是三軸滑模面組成的向量。

針對式(2)的三軸陀螺狀態方程，考慮阻尼剛度不確定及外界干擾，方程(2)可寫為

(28)

式中：dm為外界干擾；矩陣ΔC,ΔK表示系統阻尼剛度矩陣的不確定參數。式(28)整理得

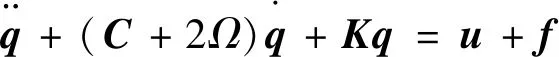
(29)

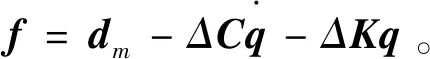
假設陀螺3個軸向的參考軌跡為xm=Axsinωxt,ym=Aysinωyt,zm=Azsinωzt。將其同樣寫成狀態方程形式，即

(30)

定義系統的狀態跟蹤誤差為

e=qm-q

(31)

定義比例-微分滑模面為

(32)

對比例-微分滑模面取一階導數

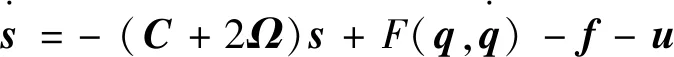
(33)

式中

理想控制律設計為

(34)

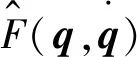
將理想控制律式(34)和式(14)代入式(33)，得閉環滑模動態為

(35)

定理3選擇理想控制律式(34)，死區補償器式(8)以及兩個RBF的權值自適應律式(26)和式(27)，則閉環控制系統的跟蹤誤差一致有界穩定。

證明：

針對式(35)的滑模動態，設計Lyapunov函數為

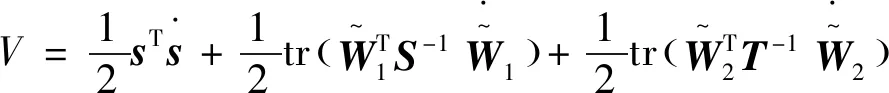
(36)

對上式求導，得

(37)

將式(35)的滑模動態代入式(37)，得

(38)

(39)

根據矩陣的跡的性質，對任一矩陣M，如下不等式成立：

則式(39)為

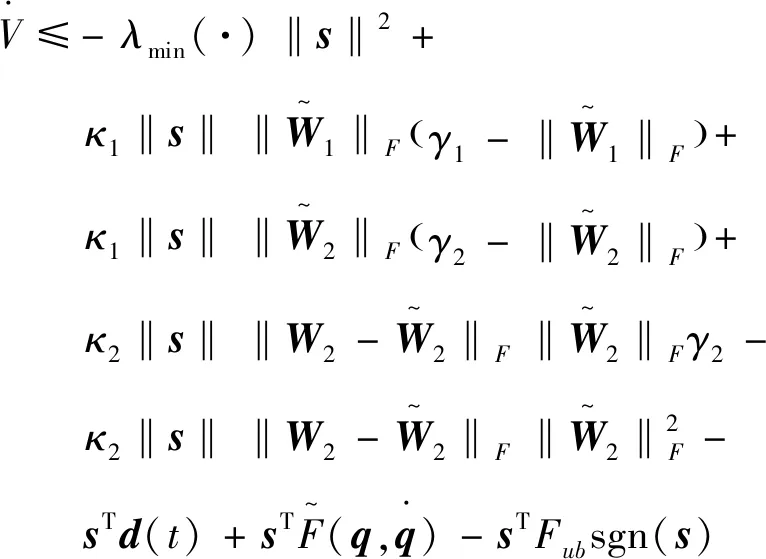
(40)

式中λmin(·)表示矩陣的最小特征值。而根據矩陣范數的三角不等式，可得

則式(40)為

(41)

考定理2，則式(41)為

(42)

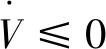
即滿足上述不等式的一組κ1,κ2可使整個閉環系統穩定。上述穩定性分析可以看出，κ1=0,κ2=0是上述不等式的一組可行解。與傳統自適應律式(26)和式(27)相比，這組可行解可以大大減弱兩個RBF網絡的權值耦合，降低控制的復雜度。因此，本文改進的權值自適應律為：

(43)

證畢。

3 仿真驗證及分析

為了驗證兩個神經網絡對未知死區的補償效果，利用Matlab/S-Function對整個陀螺閉環系統進行了仿真實驗。假設三軸MEMS陀螺儀的各項設計參數如下[7-8]：

無量綱化過程中，參考長度取q0=10-6m，參考頻率取w0=3 kHz。假設三個軸向的參考軌跡為：

xm=sint,ym=1.2sint,zm=1.5sint。

仿真過程中，滑模面比例增益c=5，控制參數Kcom=50，死區特性描述為：

正定對稱陣S,T的主對角線取值為500，RBF神經網絡隱含層結點的高斯參數中心值cj選取神經網絡輸入值范圍內的值：

c1=c2=

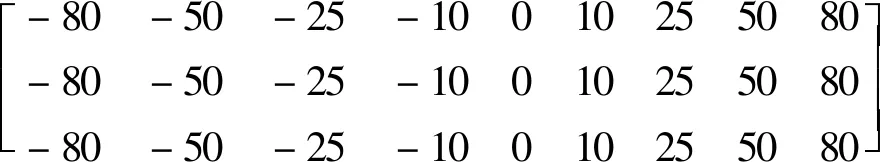
兩個RBF網絡的權值矩陣初值均設置為20。陀螺的三軸位置初始狀態設為

仿真結果如圖4—圖6所示。

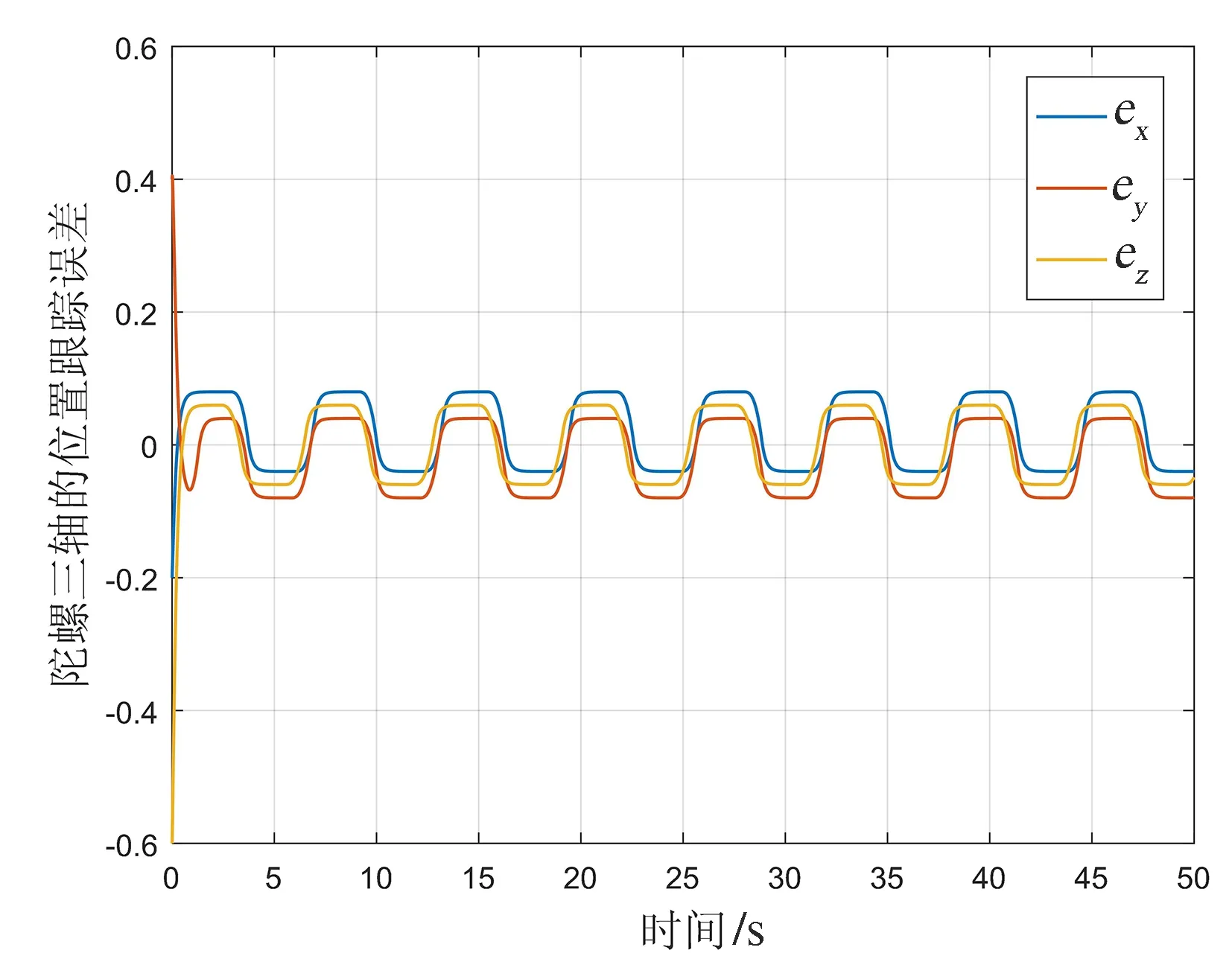
(a)無死區補償

圖5 死區補償后的各軸向控制輸入Fig.5 Triaxial control inputs with dead zone compensation

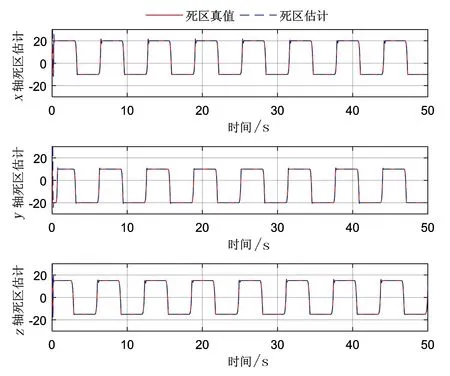
圖6 陀螺各軸向的死區估計Fig.6 Estimation of triaxial dead zone

圖4(a)表明只利用滑模控制律，不采取任何死區補償措施時，位置跟蹤誤差存在震蕩，這種震蕩反應到速度跟蹤誤差中將會造成很大的角速率精度損失；圖4(b)表明在本文的復合控制器作用下，陀螺三軸的位置跟蹤誤差可以在1 s左右收斂到0，且動靜態性能良好，說明RBF網絡對死區效應起到了很好的補償效果。

圖5為經過神經網絡補償器后各軸向的控制輸入，圖6為陀螺各軸向的死區估計結果。由圖6仿真結果可見，神經網絡補償器能夠精確估計死區邊界常數和邊界外的非線性力電函數。

4 結束語

本文針對Park S操作模式下三軸MEMS陀螺軸向軌跡跟蹤中的驅動梳齒死區問題，提出了基于權值自適應神經網絡和滑模控制的復合控制器。整個控制過程中用到兩個RBF神經網絡。穩定性分析中通過新算法設計削弱了兩個網絡的強耦合。仿真結果證明了該復合控制器能夠以較高精度估計執行器未知死區特性并實現前饋補償，保證了ParK S操作模式下MEMS陀螺三軸運動的精確跟蹤。