基于運算素養探尋一道高考真題的源與流*

洪麗敏

福建省南安第一中學 (362300)

數學運算作為數學六大核心素養之一，是指在明晰運算對象的基礎上，依據運算法則解決數學問題的素養，它不僅是現代人賴以生存的必備素質之一，也影響著其他素養的培養.在普通高中課程標準(2017年版)中，每個主題的學業要求重點必定包含培養或提高數學運算素養.

在高中數學核心素養培養過程中，教材是最基本、最重要的載體，課堂教學是訓練場，高考則是主戰場．近年來，高考命題已從基于“能力”到基于“素養”考試評價的轉變，逐步樹立“以素養立意命題”的指導思想，注重考查學生的核心素養.比如2019年全國卷Ⅰ做了較大形式的調整，導致相當一部分考生不適應，但卻很好的傳遞了一個信息——不可忽視教材和運算素養的培養.且不說網紅考題“斷臂維納斯”問題其實就在初中9年級上冊“平行線分線段成比例”的閱讀材料“黃金分割”，單說其理20題，就是教材兩道習題基于運算的組裝.

下面，筆者以2019年全國Ⅰ卷理20題為例，基于運算素養下，談談該高考試題的源與流，意在拋磚引玉.

1.高考真題展示

本題用證明的形式探求函數的零點問題，形式新穎，卻容易造成多數考生的不適應，其原因主要有：一不適應：雖是研究零點問題，但卻不是常見的“已知零點個數，逆向求參”問題；二不適應：函數f(x)的形式在全國Ⅰ卷不多見，容易蒙圈；三不適應：因題序改變，以往導數題都為21題，多數學生對(2)問本持著“放棄”的想法，如今雖調整為20題，但因沒有心理準備，學生容易缺乏繼續求解的欲望.以上種種原因導致本題得分率低下.

2.源之探——飲水思源

本題真的如考生所反應的那樣難嗎？其實不然！

讓我們先回顧一下人教A版選修2-2:第32頁B組第一題：

利用函數的單調性，證明下列不等式，并通過函數的圖象直觀驗證：

(1)sinx0,x∈(0，1).(3)ex>1+x,x≠0；(4)lnx0．

由(3)我們知道由ex>1+x,x≠0可得到ex≥x+1(x∈R)，兩邊取對數x≥ln(x+1)(x>-1)，如圖1；由(1)可知sinxx,x∈(-π，0),進而可得y=x與y=sinx在R上有且只有一個交點，如圖2；

把兩張圖整到同一坐標系，如圖3；再去掉直線y=x，如圖4.

此時我們不難發現，這個問題就是2019年全國卷Ⅰ理20題的第(2)問了.我們無法得知高考命題者是如何命制本試題的，但我們卻清楚試題的題源，那就是人手一冊的教材！

可見，無論是基礎年級的教學，或是高三年的全面復習，在培養考生數學核心素養的過程中，教材是最基本、最重要的載體，教師要注重引導學生重視教材，切不可盲目涮題，陷于“題海”而不能自拔.

3.流之拓——源遠流長

3.1 流之拓1——解題策略

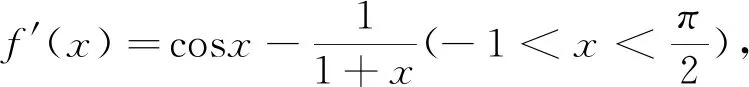
(2)略.

評析：本題(1)、(2)的解題思路類似，且對廣大師生而言并不陌生，它們都是零點問題，都離不開“零點存在定理”和“設而不求思想”，而這兩者在高考試題中屢見不鮮，如2012年全國卷Ⅰ文21題、2013年全國卷Ⅱ理21題、2015年全國卷Ⅱ理21題、2015年全國卷Ⅰ文21題、2016年全國卷Ⅱ理21題文20題、2019年全國卷Ⅰ文20題、理20題、2019年全國卷Ⅱ文21題、理20題.可見，零點問題是利用導數解決問題的重要內容，應引起廣大師生足夠的重視.

3.2 流之拓2——題源再探

從上，我們看到本題的題源之一為ex>1+x,x≠0，這是一個值得深究的問題，以該題為背景的題目比比皆是，這里不一一贅述.

教學中，我們可以引導學生往兩條線展開思考與探究：

一是代數運算方面——數學運算素養.

探究1 由ex≥x+1(x∈R)到x≥ln(x+1)(x>-1)，其實就是常見的“指對數互化運算”，借助“指對數互化運算”實現ex,x,lnx，…之間的轉化，在各地省市質檢，乃至高考命題中都屢見不鮮.比如

(2013年全國卷Ⅱ理21)已知函數f(x)=ex-ln(x+m)．

(Ⅰ)設x=0是f(x)的極值點，求m，并討論f(x)的單調性；(Ⅱ)當m≤2時，證明f(x)>0．

略解：(Ⅰ)略．(Ⅱ)當m≤2時，x∈(-m,+∞)時，ln(x+m)≤ln(x+2)，則要證明f(x)>0，只需證明當m=2時f(x)>0(加強不等式思想)．即證：f(x)=ex-ln(x+2)>0．

別證：①當-20成立；

②易證當x>-1時有ex≥1+x(當且僅當x=0時等號成立，過程略)，則有x≥ln(x+1)，則有x+1>ln(x+2)(當且僅當x=-1時等號成立)，即當x>-1時，有f(x)=ex-ln(x+2)≥(1+x)-ln(x+2)>0成立．

綜上，當m≤2時，f(x)>0成立．

探究2 加減乘除四則運算可以使數學運算更為豐滿，構造更多的函數模型.

比如由ex>1+x,x≠0可得到：①ex≥x+1，進而替換得到②ex-1≥x，兩邊取對數得③x-1≥lnx(x>0)，移項可得到④x≥lnx+1=ln(ex)，再取指數可得到⑤ex≥ex，…

二是借助圖象直觀呈現——直觀想象素養.

把探究2中5個問題用圖形表示，依次為以下圖5-圖9.

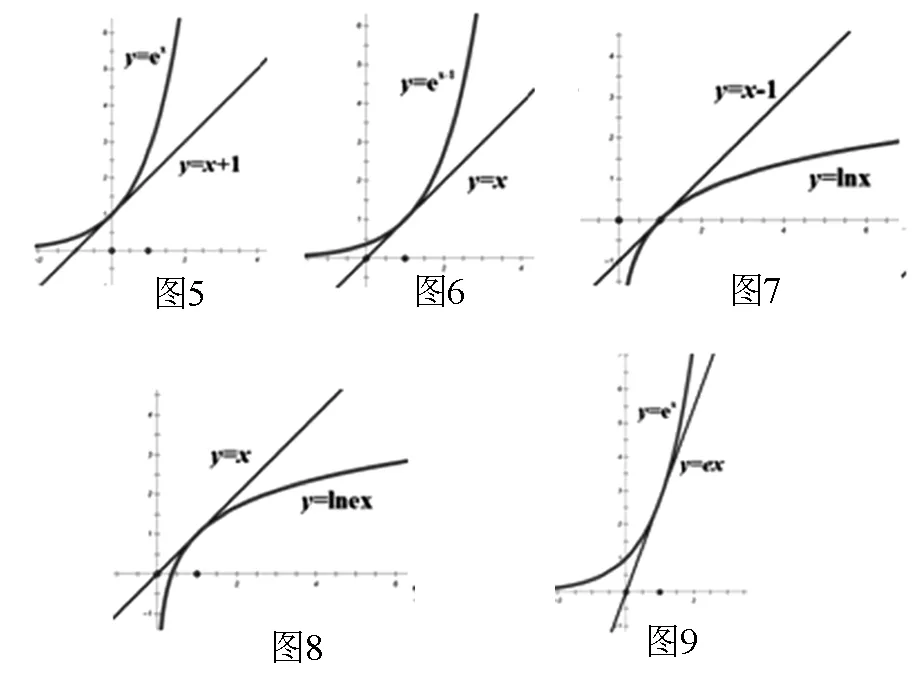
最后提煉本質——數學抽象：以上問題的本質都是研究切線問題，都可借助導數加以研究，這里就不一一探究.

面對精彩紛呈的試題，“問渠哪得清如許，為有源頭活水來”，源頭就是教材．數學教材為“教”與“學”活動提供學習主題、基本線索和具體內容，是發展學生數學學科核心素養的重要教學資源，也是高考命題的一個重要取材渠道.

值得一提的是，立足數學運算，對教材的進行開發性研究，是一種普遍適用的研究方法，也是教師教學能力自我提升的一種有效手段.教師必須在重視課本的鉆研和探究的同時加強對學生運算能力的培養，這樣，數學教學方可“源遠流長”、創新發展．