物理觀點下奔馳定理的另一種表達形式

徐 耀

浙江省紹興魯迅中學 (312030)

科學發展史表明，數學和物理自誕生起，就相互滲透，共同發展.平時我們會比較自然的用數學方法去解決物理問題，但反過來，若能從物理的角度去思考數學問題，也能起到意想不到的效果，甚至得到一些新的結論.

“奔馳定理”是平面向量中優美的一個結論，這個結論對于利用平面向量解決平面幾何問題，起著決定性的作用.本文通過三角形中頂點質量和頂點所對三角形面積的關系得到奔馳定理的另一種表達形式，及其推論.希望對解決平面向量相關問題有所幫助.

從物理學的角度看，ΔABC的某個頂點的質量越大，支點就會往這個頂點偏移，從而導致支點和此頂點所對的邊構成的三角形面積越大，也即頂點的質量與此三角形面積成“正比”關系，故筆者大膽猜測奔馳定理的另外一種表達形式：

在證明此猜想之前，先證明一個引理(三角形面積公式的行列式形式)：

下面證明定理1.

圖1

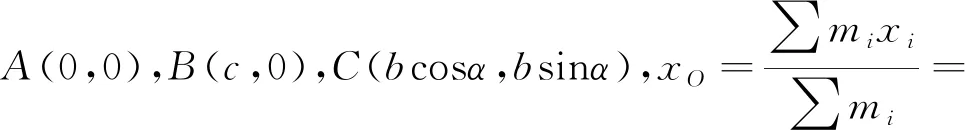
=mA∶mB∶mC.

故定理1與奔馳定理是等價的,并且由定理1可得如下推論.

同理，可得其余兩個等式.

下面例舉其應用.

圖2

圖3

圖4

圖5