隱藏于三角函數中的“向量思想”

羅世評

江西省南昌市灣里區第一中學 (330004)

首先將利用向量思想推導任意兩角差的余弦公式及“輔助角”公式如下：

結論1任意兩角差的余弦公式cos(α-β)=cosαcosβ+sinαsinβ其中(α∈R,β∈R).

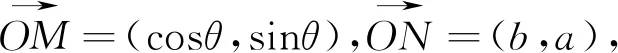
從上述兩個結論推導過程可以看出用向量思想來解決三角問題能獲得意想不到的效果，該公式的推導思路使學生能夠更好的理解“輔助角”公式的由來，也為后期更好應用該公式打下良好基礎.也體現了采用向量思想在三角中的重要地位.

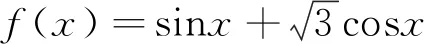
分析：本例題來源于北師大版教材第三章第二節部分，教材中采用特殊角三角函數值、正弦兩角和公式及正弦函數性質相關知識進行求解.根據本題給出的形式，不妨采用上述結論2中的向量思想求解，將會取得比較好的效果.

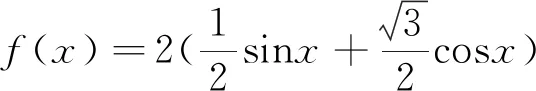
我們不妨對上述兩種“解題思路”進行分析，教材中給出的解法著重強調對兩角和差公式的結構理解和掌握，同時要求學生在“拼湊”兩角和差公式的過程中能靈活應用特殊角三角函數值,再利用正弦函數性質給出結論.而向量思想側重考察“轉化”思想，將如形asinθ±bcosθ的表達式，采用向量數量積運算來表示對應的函數，這將為解決函數最值或取值范圍問題提供更有效的方法.

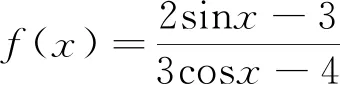
分析:通過適當的化簡得3ycosx-2sinx=4y-3，該式左邊形如asinθ±bcosθ的形式，滿足引例中的向量思想解答本題.

解析:由題意可知x∈R，原式可化為y(3cosx-4)=2sinx-3，即3ycosx-2sinx=4y-3.

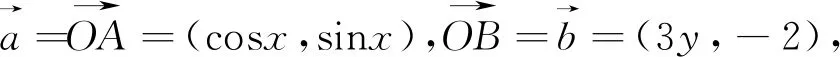
解析:由題意易知y>0，原式可化簡為ysinx=2-cosx，即ysinx+cosx=2.

例3 (教材改編)若關于x的方程(2k+3)sinx+kcosx=k+3有實根，求實數k的取值范圍.

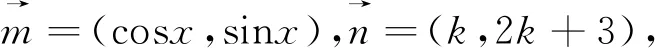
從上面的3個例題中我們不難發現，如將三角問題進行適當的化簡處理，使原式轉化成形如asinθ±bcosθ的形式，使用向量思想也將可以完美解決函數最值或取值范圍相關問題，并得到取等號時的對應條件.這使得我們在實際教學中，面對“輔助角”公式的理解和應用感到困惑的學生，提供了一條不錯的途徑.

分析:考慮到使用向量思想表示函數，不妨將原式變形為求f(x)-1=(1+sinx)(1+cosx)，利用單位圓，把函數取值與相應四邊形或三角形面積聯系起來考慮，通過求面積大小來得到f(x)最值.

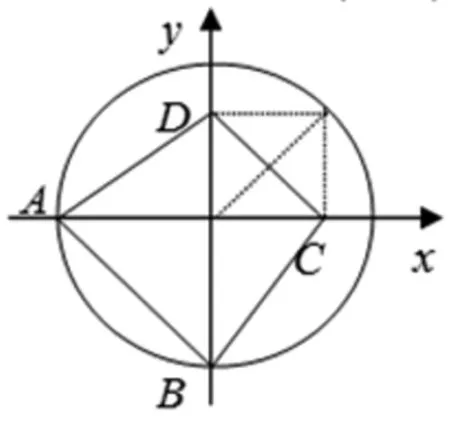
圖1

解析:如圖1，在單位圓和直角坐標系中，不妨記

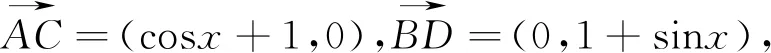
圖2 圖3

例5 (2018年全國Ⅰ理科)已知函數f(x)=2sinx+sin2x，則f(x)的最小值.

分析:通過化簡知f(x)=2sinx(1+cosx),從形式看和例4有類似之處，利用單位圓，可將函數f(x)取值與對應的三角形ΔABC面積聯系起來，利用三角形面積最值問題來求解f(x)的最小值.

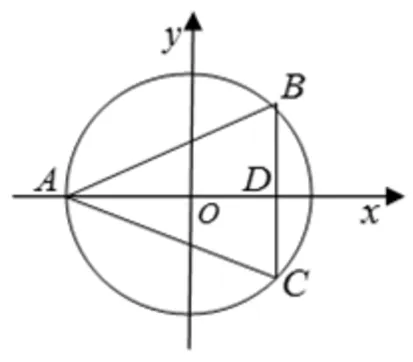
圖4

解析:如圖4，通過單位圓不妨A(-1,0),B(cosx,sinx)，C(cosx,-sinx)，

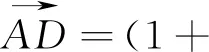
評注：從以上例4、例5應用向量思想求解三角問題的過程可以看出，當我們恰當的利用單位圓上點坐標的特點和向量相關知識，使得三角函數問題與對應的幾何圖形面積聯系起來，從而為我們提供了一種用幾何方式解答三角問題的重要思想.