領會考點 研究題型 提升學生的解題能力
——以蘇科版教材“平面解析幾何”為例

徐 崇

(江蘇省常熟市梅李高級中學 215500)

高中數(shù)學教學面臨的一個根本任務，就是在立德樹人和核心素養(yǎng)培育的背景之下，培養(yǎng)學生的解題能力.這樣的教學定位，意味著要將立德樹人與核心素養(yǎng)培育，與很現(xiàn)實的培養(yǎng)學生的解題與應試能力結(jié)合在一起.而這也就意味著在日常的教學中，教師要重視學生的數(shù)學知識及其體系的建構(gòu)，同時又要在此基礎上切實培養(yǎng)學生的解題能力.面對這一任務，有研究者明確指出高中數(shù)學教師要基于新時代高考的核心功能和主要任務，進而領會《普通高中數(shù)學課程標準(2017年版)》《2018年普通高等學校招生全國統(tǒng)一考試大綱(理科數(shù)學)》的精神，研究普通高等學校招生全國統(tǒng)一考試數(shù)學卷中試題與服務選才這“一把尺”之間的關系，從高考解析幾何試題中分析考查題型、內(nèi)容、熱點等角度展開研究，從而尋找到關于高考數(shù)學知識的基本考向以及備考思路.本文試以蘇科版教材“平面解析幾何”為例，談談筆者的探究過程與結(jié)果，以期對同行的相關研究起到拋磚引玉的作用.

一、領會考點，奠定解題能力提升的基礎

平面解析幾何是高中數(shù)學知識體系中的基礎性知識，同時也是高考的必考內(nèi)容，平面解析幾何的基本思想實際上是用代數(shù)方法解決幾何問題.從當前高考實際情況來看，幾何性質(zhì)考查內(nèi)容主要以離心率為主，而相應的學生學習的難點主要與取值范圍、最值等問題相關.也正因為這個原因，圓錐曲線的離心率、取值范圍和最值問題成為平面解析幾何知識考查的重要指向.這實際上是從考點的角度，對平面解析幾何知識進行的研究，而要培養(yǎng)學生的解題能力，首先就必須以考點知識的領會來奠定解題能力培養(yǎng)的基礎.

從宏觀角度來看，平面解析幾何部分的知識涉及到的考點雖然很多，但與圓錐曲線相關的考點，由于其具有綜合性，以及利用圓錐曲線相關知識解決問題時能夠涉及比較廣泛的知識，因而既表現(xiàn)出一定的解題難度，又表現(xiàn)出相應的解題能力培養(yǎng)的空間.

當然作為對考點的研究，面向培養(yǎng)學生解題能力的需要，還必須研究更加細致的“點”.比如說，橢圓中的最值問題包括兩種：一種是參數(shù)的取值范圍問題，另一種是長度與面積的最值問題.最值問題一般都與動態(tài)變化相關，因此在解題的時候要引導學生認識到，前者往往需要根據(jù)圖形的幾何特征去建立起與某個參數(shù)相關的不等式或者函數(shù)，而后者則主要是通過建立關于某個參數(shù)的函數(shù)，然后運用基本不等式或函數(shù)知識去求解的.當然最終能力的形成，在于學生具體的練習過程，而這就涉及到題型研究.

二、研究題型，鋪就解題能力提升的大道

通常情況下教師對題型研究往往進行得比較深，比較透，但筆者在教學中發(fā)現(xiàn)，要想有效地培養(yǎng)學生的解題能力，還必須帶著學生去研究題型，要讓學生對題型有非常感性的認識，這樣他們在解題的時候才能做到心里有數(shù).如果把解題和考試比作打仗，那對題型的研究實際上就是為了做到知己知彼而百戰(zhàn)不殆.

例如有這樣一道題目：已知點A(-2，0)、B(2，0)，動點M(x，y)滿足直線AM與BM的斜率乘積為-1/2.記M軌跡為曲線C.(1)求C的方程，并說明C是什么曲線；(2)過坐標原點的直線交C于P、Q兩點，點P在第一象限，PE⊥x軸，垂足為E，連接QE并延長交C于點G.(ⅰ)證明:△PQG是直角三角形;(ⅱ)求△PQG面積的最大值.

雖然這是全國卷上的題目(2019年高考全國Ⅱ卷理科第21題)，但是筆者認為其對江蘇的考生也有一定的指導作用.這道試題考查了曲線的方程、直線和橢圓的位置以及最值問題，考查的是學生分析問題與解決問題的能力.在問題解決的過程中，涉及到邏輯推理、直觀想象、數(shù)學運算等數(shù)學核心素養(yǎng)；從實際解題的角度來看，試題解法靈活，內(nèi)涵豐富，綜合性強，為不同學生搭建了施展才能的舞臺，是一道好題.認為它是好題，還有一個重要的原因，這就是這是一種有代表性的題型，這一題型所涵蓋到的平面解析幾何知識，以及涉及到的解題能力，都能夠讓學生在解題的過程中，獲得知識的鞏固與能力的提升.

比如說，在具體的解題過程中，可以讓學生遵循一題多解的思路，將題目中給出的信息與問題，與原有的解題經(jīng)驗結(jié)合起來，以從多個角度尋找問題解決的方法.筆者在課堂上引導學生解題的時候，選擇了這樣幾個角度(限于篇幅，這里以第2問為例)：

角度1：讓學生先設出直線PQ的斜率為k，然后得出直線的方程，也就是y=kx(k>0)，然后與此前得到的C的方程聯(lián)立，就可以求出x(用k來表示)；其后經(jīng)過幾次代換之后，則可以得到一個以k為系數(shù)的方程，即(2+k2)x2-2uk2x+u2k2-8=0；再然后就可以借助于韋達定理與斜率的知識求解.這個過程中，多次化簡與消元，并借助于函數(shù)的單調(diào)性求出了△PQG面積的最大值.此過程中學生的思維量極大，多次轉(zhuǎn)換才能實現(xiàn)難點的突破，這實際上就賦予了學生一個充足的培養(yǎng)自身解題能力的空間.

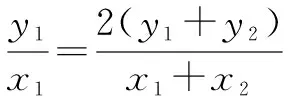
這是兩個不同的解決問題的角度，盡管在課堂上花費一定的時間，但是無論是涉及到的數(shù)學解題方法，還是運用到的數(shù)學知識，都能夠有效地幫學生拓寬眼界，提升學生的解題層次，從而提升學生的解題能力.

三、因材施教，落實解題能力提升的要求

在實際教學中筆者發(fā)現(xiàn)，由于學生之間的個體差異，同樣一個考點的確定與相應的題型的選擇，不同學生在訓練的過程中，表現(xiàn)出來的接受能力以及解題能力的提升幅度是有所差異的.從這個角度來看，高中數(shù)學教師要想切實提升學生的解題能力，就必須做到以生為本而因材施教.

如同上面所強調(diào)的一樣，平面解析幾何一直是高中數(shù)學的重要內(nèi)容之一，在歷年的高考中也都是考查的重點，因此這是我們高考復習的重頭戲.從近幾年江蘇高考的情況來看，涉及到平面解析幾何的題目還是比較豐富的，本質(zhì)上這是因為平面解析幾何知識內(nèi)容較多，方法性、思想性都很強，因此高中數(shù)學教師要在高三復習中提升復習效率，就必須有策略地部署復習安排.筆者在教學中，關于這一知識所進行的復習部署中，很重要的一點就是先去研究學生個體.當然由于班級授課制的關系，再加上所教班級不止一個，因此也不可能真正地面向每一個個體進行研究.但是將學生分成不同的層次，研究每一個層次學生在平面解析幾何知識的學習中，所表現(xiàn)出來的知識理解能力、思維能力等，然后去實施教學，就可以取得比較好的效果.

總的來說，面向?qū)W生解題能力的提升需要，并在此基礎上滿足學生數(shù)學學科核心素養(yǎng)培育的需要，數(shù)學教師就必須認真研究考點，準確把握題型，然后再面向不同層次的學生，施以不同的解題教學策略，這樣就可以切實提高學生的解題能力.而且事實表明，這樣的教學思路是能夠滿足絕大多數(shù)學生的需要的，學生對這樣的教學方式也是比較歡迎的，從教學效果的角度來看，堅持使用這樣的教學思路，學生的解題能力可以得到明顯提升，而數(shù)學學科核心素養(yǎng)也能夠在這樣的過程中得到培養(yǎng).