三道賽題的有趣推廣
2020-10-19 09:23:36武增明
數理化解題研究 2020年28期
武增明
(云南省玉溪第一中學 653100)
此題可以推得以下有趣的推廣命題.
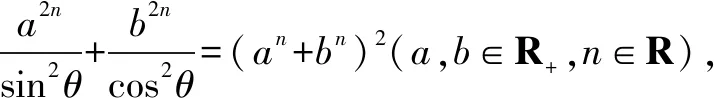
證明由柯西不等式，得
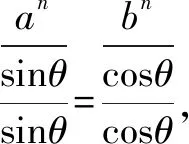
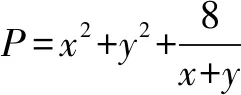
此題可以推得以下有趣的推廣命題.
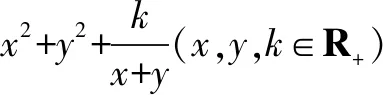
證明由二元及三元均值不等式，得
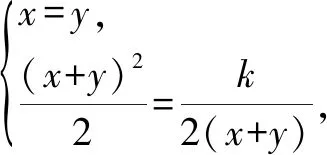
說明由推廣命題的證明可以看出，原賽題中的條件x3+y3=2是多余的.
賽題3(2016年全國高中數學聯合競賽湖北省預賽高一賽題)如果存在實數a，使得關于x的不等式acosx+bcos2x>1無實數解，那么實數b的最大值為____.
此題可以推得以下有趣的推廣命題.
命題設c為正常數，如果存在實數a，使得關于x的不等式acosx+bcos2x>c無實數解，那么實數b的最大值為c.
證明因為關于x的不等式acosx+bcos2x>c無實數解，所以關于x的不等式acosx+bcos2x≤c的解集為R.
所以取x=0，得a+b≤c；取x=π，得b-a≤c.
兩式相加，即得b≤c.
當b=c時，取a=0，此時原不等式為cos2x>1，顯然無解.所以實數b的最大值為c.
