全陶瓷球軸承接觸分析與試驗(yàn)研究

周井玲，王新鵬，李 昕

（南通大學(xué)機(jī)械工程學(xué)院，江蘇 南通 226019）

1 引言

隨著科學(xué)技術(shù)的快速發(fā)展，滾動(dòng)軸承的使用范圍越來越廣，對(duì)滾動(dòng)軸承的性能要求越來越高，尤其是在一些特殊環(huán)境下，例如高溫、低溫、強(qiáng)酸、高速、無潤(rùn)滑等，傳統(tǒng)的鋼制軸承已經(jīng)滿足不了這些需求[1]。當(dāng)軸承在轉(zhuǎn)動(dòng)過程中遇到貧油和斷油情況時(shí)，容易發(fā)生軸承抱死，造成事故，而全陶瓷軸承因具有自潤(rùn)滑能力，磨擦系數(shù)較低，因此全陶瓷軸承在潤(rùn)滑油不足稀少時(shí)，潤(rùn)滑能力也不輸潤(rùn)滑良好傳統(tǒng)鋼軸承[2]。

現(xiàn)以型號(hào)6004 全陶瓷深溝球軸承和鋼制深溝球軸承為研究對(duì)象，對(duì)其進(jìn)行進(jìn)行接觸分析與疲勞壽命試驗(yàn)，比較這兩種軸承在無油潤(rùn)滑下的運(yùn)行狀況。

2 接觸應(yīng)力分析

2.1 赫茲接觸應(yīng)力理論

對(duì)于只受徑向力Fr作用的球軸承，其滾動(dòng)體所受最大載荷計(jì)算公式為：

式中：Fr—軸承所受徑向載荷；Z—軸承滾動(dòng)體數(shù)目；α—接觸角。

軸承在未收到載荷作用時(shí)，接觸形式為點(diǎn)接觸，其接觸幾何關(guān)系，如圖1 所示。同時(shí)規(guī)定凸面曲率為正，凹面曲率為負(fù)，則主曲率代和：

主曲率差函數(shù)：

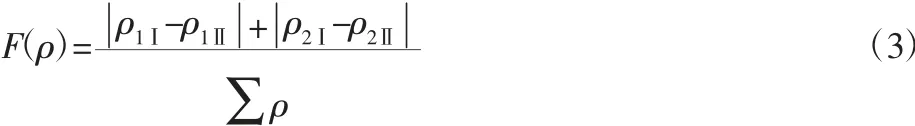
圖1 軸承接觸幾何關(guān)系Fig.1 Geometric Relationship of Contact of Bearing

根據(jù)赫茲理論，對(duì)軸承施加載荷后，其接觸區(qū)域一般為橢圓，且在接觸區(qū)域內(nèi)接觸應(yīng)力按半橢球分布，如圖2 所示。

圖2 接觸區(qū)域應(yīng)力分布Fig.2 Stress of Distribution of Contact Area

接觸區(qū)域長(zhǎng)半軸a、短半軸b 的計(jì)算公式為：

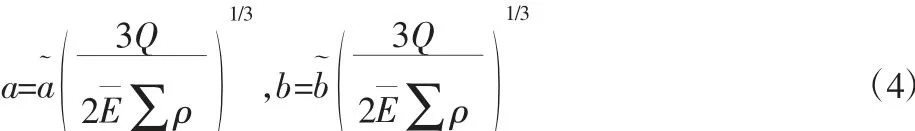
式中：a~，b~—與F（ρ）相關(guān)的系數(shù)；Q—滾動(dòng)體所受載荷；Eˉ—當(dāng)量等

效彈性模量。

將接觸面應(yīng)力沿橢球面接觸區(qū)域進(jìn)行積分，可得最大接觸應(yīng)力P0：

2.2 接觸應(yīng)力有限元分析

2.2.1 建立有限元模型