基于支持向量機模型的價值投資策略分析

摘要：傳統(tǒng)機器學習算法在量化投資上的應用大多是數(shù)據(jù)挖掘式的全盤決策，但較少被用于優(yōu)化現(xiàn)有金融學定價模型。因此，本文提出一種基于支持向量機的優(yōu)化多因子價值投資模型，該模型首先以估值、質(zhì)量類因子作為評分指標構(gòu)建多因子價值投資模型，再將基于價值因子的多維指標作為輸入變量，訓練并建立多截面期支持向量機模型。通過對各期候選股進行0-1預測分類，選取“未來20日夏普率高居前30%”的1類股票構(gòu)建優(yōu)化投資組合;最后依據(jù)技術指標構(gòu)建動態(tài)倉位調(diào)整法則，以達到控制風險及回撤的目的。實證結(jié)果表明：在70%的調(diào)整倉位下，策略最終年化收益為25.08%，夏普率為1.24，遠超同期滬深300指數(shù)。

關鍵詞：價值投資 多因子模型 支持向量機 技術指標

一、 引言

量化投資是依據(jù)技術指標、基本面及宏觀經(jīng)濟指標數(shù)據(jù)，通過建立某種數(shù)學模型或算法預測資產(chǎn)價格的趨勢變化并從中獲利的投資方式，其盈利能力的邏輯支撐來自于Sharpe（1964）[1]提出的資本資產(chǎn)定價模型（CAPM）。在M-V準則基礎上，該模型將證券的期望收益分解為無風險收益與證券特有風險的溢價;作為多因子模型的最簡單形式，CAPM改變了投資者看待證券收益組成的方式，“Seeking Alpha”的策略成為量化投資的最初嘗試;Ross（1976）[2]提出套利定價理論（APT），并在非均衡條件下推導出多因子模型，而CAPM模型自然成為其一個特例。自此，尋找恰當數(shù)量的有效因子并通過定價模型進行證券估值的量化投資策略主導了學界及商界的市場實踐，如：Fama、French（1993）[3]通過研究發(fā)現(xiàn)：SML、HML因子及Beta系數(shù)能夠顯著地解釋證券的超額收益。量化投資的發(fā)展離不開其核心假設，即歷史數(shù)據(jù)與證券價格的未來走勢存在某種關聯(lián)關系，然而越來越多的研究與實踐證明，依賴線性關系的傳統(tǒng)定價模型在逐漸有效的市場中出現(xiàn)了“失靈”的現(xiàn)象。

機器學習算法依據(jù)嚴謹?shù)臄?shù)據(jù)輸入、模型訓練及預測方法，恰能通過高維數(shù)據(jù)指標描述證券截面特征，并尋找各維度間隱含的非線性關系。由于其優(yōu)秀的分類預測能力，機器學習算法被廣泛地運用于量化選股與擇時之上。

作為“預測統(tǒng)計學”體系的發(fā)展成果之一，支持向量機強調(diào)結(jié)構(gòu)風險最小化，因此解決了神經(jīng)網(wǎng)絡等算法中存在的“過學習”理論缺陷，具有非常優(yōu)秀的泛化能力。因其在二分類上的優(yōu)秀能力，支持向量機經(jīng)常被用于預測股市漲跌情況。王彥峰等（2006）利用滾動窗口方法構(gòu)建支持向量機預測模型，準確預測了個股日均價;張玉川等（2007）將技術指標作為輸入變量對個股股價進行漲跌預測，其預測準確率大于60%;徐國祥等（2011）在傳統(tǒng)SVM基礎上引入主成分分析及遺傳算法，經(jīng)優(yōu)化后模型對我國股指的預測準確率較高;賽英等（2013）使用遺傳算法和粒子群算法優(yōu)化支持向量機模型，并構(gòu)建了股指期貨回歸預測模型;李斌等（2017）使用技術指標作為輸入變量，比較了不同算法模型的收益預測情況，其中SVM模型策略的夏普率超過1.38，收益能力最高;呂凱晨等（2019）利用SVM優(yōu)化多因子模型，其策略年化收益大于20%，遠超同期大盤指數(shù)表現(xiàn)[4-9]。

總結(jié)以上文獻，可以發(fā)現(xiàn)以下值得改進之處：

第一，利用支持向量機模型進行全權(quán)投資決策的方法在一定程度上忽略了傳統(tǒng)金融學理論對投資決策的指導作用，因此模型的高預測準確度或許僅是數(shù)據(jù)挖掘的產(chǎn)物;

第二，在弱有效市場假說成立時，使用技術指標作為訓練樣本維度所構(gòu)建的模型將只能獲得市場平均收益;

第三，證券實際價格分布的峰度與偏度具有顯著的時變性，因此在預測多截面期股價漲跌時，依據(jù)固定樣本建立的支持向量機模型預測能力有限。

鑒于上述文獻中存在的缺陷，本文提出以下改進措施：

第一，構(gòu)建多因子-支持向量機聯(lián)合優(yōu)化模型，將機器學習算法與傳統(tǒng)金融學理論模型進行對等融合;

第二，嘗試摒棄技術指標，引入“安全邊際”“內(nèi)在價值”等價值投資理念因子作為模型訓練數(shù)據(jù)的維度指標，使模型預測準確率具有更顯著的經(jīng)濟學解釋意義及理論支撐;

第三，使用滑動窗口的訓練樣本更新方法建立各截面期支持向量機模型，解決單一樣本訓練模型在進行長期預測時準確度低的問題;使用網(wǎng)格搜索方法更新最優(yōu)參數(shù)，提高模型預測準確度。

二、 多因子價值投資模型

（一）價值投資因子

構(gòu)建多因子模型的兩大核心在于：第一，多因子模型中各因子的解釋意義是否具有理論支撐;第二，所挑選的因子是否具備超額收益預測能力。據(jù)此，本文以因子評分法構(gòu)建多因子價值投資模型，模型建立方法如下：

第一步，以價值投資理念為基礎，圍繞估值與質(zhì)量維度篩選因子。由于以相對價格、盈利能力、利潤增長率為基礎的三要素定價法是證券數(shù)量化分析的關鍵，因此分析維度如下：

1.內(nèi)在價值，企業(yè)價值體現(xiàn)在：企業(yè)具有長期可持續(xù)競爭的行業(yè)優(yōu)勢，且盈利狀況穩(wěn)定;

2.安全邊際，即相對于其內(nèi)在價值，證券價格相對合理。具有較高安全邊際的證券能夠為投資者提供良好的價格下跌緩沖[10]。

本文基于價值因子、估值因子兩大維度對證券的內(nèi)在價值及安全邊際進行篩選[2]，并以此構(gòu)建多因子模型。將多因子模型的候選因子定為如下3大類共9個因子，它們綜合考慮了企業(yè)的估值、成長、質(zhì)量三個維度。

第二步，測試因子有效性。對所選因子進行有效性檢驗，以保證各因子具有顯著的超額收益解釋能力。本文利用IC、IR值檢驗因子有效性。因子IC值指因子t期暴露與證券t+1期證券收益率的相關系數(shù)，其絕對值越高，則意味著該因子具有較強的收益預測能力;IR值則由下式給出：

其中表示投資組合的夏普率平方和，表示消極投資組合的夏普率平方和，最后項為IR值（Information Ratio），是積極投資組合的alpha收益除以其標準差。IR值衡量主動證券分析帶來的額外回報，是驗證因子有效性的另一維度[11]。

利用滬深300指數(shù)成分股計算候選因子IC均值、IR值，結(jié)果如下。

除凈現(xiàn)金流量增長率外，其余因子的12周期IC均值絕對值均超過0.015，表明因子暴露與股價未來收益具有顯著相關性。

第三步，剔除冗余因子。估值與質(zhì)量因子之間經(jīng)常存在高相關性，為了防止因子相關造成的選股同質(zhì)性問題，對上述9個候選因子進行相關系數(shù)分析。因子相關系數(shù)矩陣如下：

市凈率與市現(xiàn)率、5年凈資產(chǎn)收益率與資產(chǎn)回報率、每股收益、每股股息的相關系數(shù)均大于0.85。在對比因子IC均值、IR值后，舍棄IC均值較低的市現(xiàn)率和5年凈資產(chǎn)收益率。

（二）多因子價值投資模型

依據(jù)上節(jié)篩選出的候選因子建立多因子模型，步驟如下：

1.區(qū)分候選因子的方向性，將資產(chǎn)回報率、每股收益等效益型指標劃分為正向因子;將市盈率、市凈率等成本型指標劃分為負向因子。區(qū)分方向性對多因子評分的準確性具有重大意義;

2.在各截面期，依據(jù)滬深300指數(shù)成分股的各因子值排名進行評分[12]。以正向因子為例，在t截面期，i股票的第j個因子的評分為：

其中表示i股票在t截面期j因子的因子值排名;

3.對股票各因子得分進行基于該期因子IC值的權(quán)重求和，獲得綜合得分;選取得分最高的50只股票作為該截面期的候選股票，等權(quán)重分配資金形成投資組合;在每個截面期重復上述操作。

多因子價值投資模型的收益結(jié)果如下。（相關回測數(shù)據(jù)由Auto-Trader提供）模型在2017年1月1日——2019年4月1日獲得超過35.9%的累計收益，年化收益為15.21%，夏普率達0.75。

三、基于支持向量機的多因子優(yōu)化模型

支持向量機（Support Vector Machine）是由基于結(jié)構(gòu)風險最小化原理的機器學習算法，從原理上克服了傳統(tǒng)機器學習算法存在的維數(shù)災難與“過學習”等問題。支持向量機的思路即在特征空間中尋找使樣本點間距最大化的超平面;在非線性可分情況下，可以使用核函數(shù)映射方法，將原始特征空間映射至高維空間以尋找最優(yōu)超平面（高維問題即可被歸結(jié)為求解凸規(guī)劃問題）。

因其在非線性、高維問題中具有較強的延拓能力，本文引入支持向量機對證券收益特征進行預測及分類。下文先簡述支持向量機的原理，再將其應用于優(yōu)化多因子模型的選股步驟。

（一）線性支持向量機

在線性可分情況下，考慮給定共有m個樣本的訓練樣本集：

;

每個樣本位d維向量，有d個觀測值，即。分類超平面可以通過以下現(xiàn)象方程來描述：

其凸二次型規(guī)劃問題的方程組如下：

利用拉格朗日乘子法，即得到其對偶問題;通過拉格朗日乘子（）變換，該問題化簡為如下函數(shù)：

其中。令對和的偏導數(shù)為零，最終聯(lián)立兩式、解出、求出和，即得到預測模型：

下圖是簡單線性支持向量機分類器示例。

圖2 線性可分情況下的SVM

（二）非線性支持向量機

在非線性情況下，通過核函數(shù)變換將原始特征空間映射至高維空間，即可將非線性可分問題轉(zhuǎn)換為高維空間中的線性可分問題。同上理，其預測模型如下：

其中核函數(shù)。由于實際計算并不需要在高維空間進行，因此其復雜度并未提高。常見核函數(shù)有線性核函數(shù)、Sigmoid核函數(shù)、高斯核函數(shù)等。經(jīng)驗表明，高斯核函數(shù)通常具有較高準確度，本文將其作為構(gòu)建支持向量機的核函數(shù)[13-15]。

（三）模型構(gòu)建

基于上述原理，支持向量機模型構(gòu)建流程如下：

1.數(shù)據(jù)獲取。①股票池：滬深300指數(shù)成份股及其相關因子數(shù)據(jù)，每只股票在某截面期的價格及相關因子數(shù)據(jù)為一個樣本;②初始訓練樣本區(qū)間：2016年1月1日至 2016年11月30日共 11個月作為訓練樣本，并對接下來2個月內(nèi)候選股票未來20日夏普率進行分類預測。在完成一次訓練-預測后，固定訓練集長度為11個月，進行步長為2個月的滑動窗口訓練集更新;③回測時間：2017年1月1日至2019年4月1日，共28個截面期。

2.特征和標簽提取。每個自然月第一個交易日股票各大類因子數(shù)據(jù)作為訓練樣本的特征集，股票未來20日夏普率作為訓練樣本標簽：未來20日夏普率排名前30%的股票標記為1類，排名后30%的股票標記為0類。

3.特征標準化。對各類因子數(shù)據(jù)進行Z-Score標準化，消除量綱影響。

4.訓練。在各截面期（每月第一個交易日）選取未來20日夏普率排名前、后30%的股票分別作為正例與負例、使用網(wǎng)格搜索、交叉驗證方法，在每截面期更新最優(yōu)參數(shù)，以保證各截面期模型對于其所訓練樣本具有最高預測準確率。

5.構(gòu)建投資組合。若多因子價值投資模型的50只候選股票中存在“未來20日夏普率”預測為1類的股票，則等資金權(quán)重買入所有1類股票，構(gòu)建優(yōu)化投資組合;對已有持倉股票中預測為0類的股票進行清倉操作。

（四）策略結(jié)果

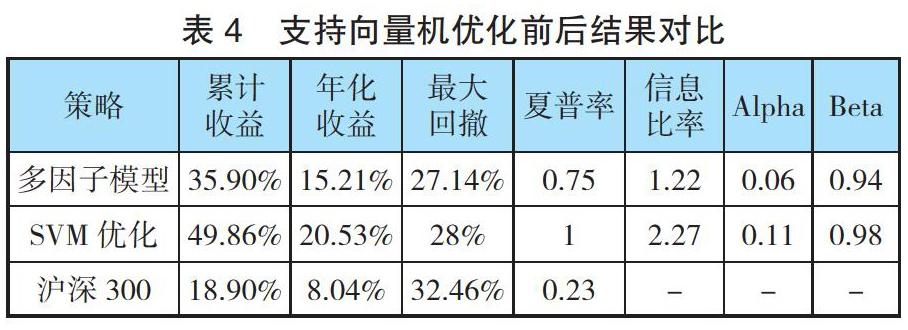
經(jīng)支持向量機分類優(yōu)化后，模型回測結(jié)果如下。

模型回測期內(nèi)累計收益近50%，年化收益為20.51%，信息比率為2.27。滑動周期、網(wǎng)格尋參下的支持向量機選股模型的平均預測準確率達70%，模型的收益效果顯著提高。

（五）基于移動均線的動態(tài)倉位調(diào)整方法

技術分析指標泛指以證券價格為基礎、通過某種數(shù)學公式衍生得出的價格指標。雖然有效市場假說的最簡單形式足已否決技術分析獲取超額收益的能力（Fama，1965）[16-17]，但大量文獻及市場實踐證明：第一，我國證券市場遠不及弱有效（趙子銘，2019）[18];第二，投資者仍能通過移動平均線（MA）、異同移動平均線（MACD）在內(nèi)的技術指標進行趨勢獲利 [19]。支持向量機優(yōu)化后的選股模型具有較高預測準確度和遠超大盤的盈利能力，但其回撤、波動率較大，在實際投資中會對投資者帶來巨大心理壓力，從而導致非理性投資行為。因此本文嘗試利用技術指標信號對投資組合的倉位進行動態(tài)調(diào)整，以控制策略的風險敞口。

本文使用滬深300指數(shù)MA5、MA60移動平均線判斷股市漲跌趨勢。移動均線間的相對走勢能夠提供客觀的擇時信號，因此可以通過其趨勢預測資產(chǎn)價格的變化拐點：以移動平均線的金叉、死叉作為牛市和熊市的轉(zhuǎn)換條件進行必要的擇時操作[20]。具體操作為：

在每一調(diào)倉截面期判斷滬深300指數(shù)MA5與MA60的相對走勢;若形成金叉，則使用全倉策略構(gòu)建投資組合;若形成死叉，則將倉位動態(tài)調(diào)整為某一固定比例（分別使用70%、50%、30%，空倉作為調(diào)整比例實現(xiàn)策略）。策略結(jié)果如下表所示。

投資實踐常用70%倉位作為動態(tài)調(diào)整比例。在此方法下，模型在原SVM優(yōu)化模型基礎上累計收益為65.07%、年化收益為25.08%、夏普率為1.24，且最大回撤下降至24.21%。

經(jīng)優(yōu)化后的多因子—支持向量機模型具有良好的分類預測能力，且其回撤風險被有效控制，為投資者提供了良好的市場實踐參考價值。同時，將支持向量機作為防范與監(jiān)控我國證券市場系統(tǒng)性風險的預測手段，或能豐富與完善決策者現(xiàn)有的風險調(diào)控機制，為我國資本市場的健康發(fā)展提供重要參考。

四、結(jié)論

本文以滬深300指數(shù)成分股及相關數(shù)據(jù)為研究對象，使用支持向量機對傳統(tǒng)多因子模型的選股步驟進行分類-預測優(yōu)化，提高了策略收益能力;提出基于移動均線的動態(tài)倉位調(diào)整方法并有效控制了投資策略的風險敞口。對應于引言中提出的前人文獻不足之處，本文通過實踐得出以下結(jié)論：

第一，通過滑動窗口、網(wǎng)格尋參方法建立的多截面期支持向量機優(yōu)化模型在量化選股中具有優(yōu)秀的分類預測能力;策略最終年化收益為25.08%、夏普率為1.24，預測準確度較高;多因子-支持向量機聯(lián)合優(yōu)化模型的理論邏輯與預測可信度都優(yōu)于將算法、數(shù)據(jù)與金融學理論剝離的傳統(tǒng)“數(shù)據(jù)挖掘式”方法;

第二，與使用技術指標的文獻相異，本文使用價值投資因子作為輸入數(shù)據(jù)的維度指標，所建立的支持向量機模型具有優(yōu)秀的分類預測能力，表明模型能夠發(fā)掘傳統(tǒng)價值投資及因子估值模型中未能被描述的隱性關系。

隨著我國資本市場的日益發(fā)展與成熟，市場有效性將侵蝕以技術指標、基本面分析等方法獲取超額收益的機會，而支持向量機在內(nèi)的機器學習算法或許能為投資者帶來超越市場平均收益的新機遇。

未來，本文作者擬在如下幾個方向進行深入研究：第一，嘗試使用更高維度的基本面信息作為輸入變量，以期能更全面描述證券的價格動量、盈利指標、流動性等特征，提升模型的預測效果;第二，嘗試使用其他機器學習算法尋找傳統(tǒng)因子模型中未能被線性解釋的證券超額收益。

參考文獻：

[1]Sharpe，W.F.Capital Asset Prices：A Theory of Market Equilibrium under Conditions of Risk[J].Journal of Finance，1964，19：425-442.

[2]Ross，Stephen（1976）.The arbitrage theory of capital asset pricing[J].Journal of Economic Theory 13 （3）; 341-360.

[3]Fama E F，F(xiàn)rench K R.Common risk factors in the returns on stocks and bonds[J].Journal of Financial Economics，1993，33 （1）：3-56.

[4]王彥峰，高風.基于支持向量機的股市預測[J].計算機仿真，2006（11）：256-258+321.

[5]張玉川，張作泉.支持向量機在股票價格預測中的應用[J].北京交通大學學報，2007（06）：73-76.

[6]徐國祥，楊振建.PCA-GA-SVM模型的構(gòu)建及應用研究——滬深300指數(shù)預測精度實證分析[J].數(shù)量經(jīng)濟技術經(jīng)濟研究，2011，28（02）：135-147.

[7]賽英，張鳳廷，張濤.基于支持向量機的中國股指期貨回歸預測研究[J].中國管理科學，2013，21（03）：35-39.

[8]李斌，林彥，唐聞軒.ML-TEA：一套基于機器學習和技術分析的量化投資算法[J].系統(tǒng)工程理論與實踐，2017，37（05）：1089-1100.

[9]呂凱晨，閆宏飛，陳翀.基于滬深300成分股的量化投資策略研究[J].廣西師范大學學報（自然科學版），2019，37（01）：1-12.

[10]本杰明.格雷厄姆，聰明的投資者[M].北京：人民郵電出版社，2010：1-289.

[11]Bodie，Z.，Kane，A.and Marcus，A.（2014）.Investments-Global Edition.London：McGraw Hill Higher Education.

[12]Piotroski J D.Value investing：The use of historical financial statement information to separate winners from losers[J].Journal of Accounting Research，2000 ：1-41.

[13]汪夢竹.基于支持向量機的股票量化交易策略研究[D].重慶大學，2018.

[14]Vapnik V.N，1995，The Nature of Statistical Learning Theory [M].New York ：Springer.

[15]宋文達.基于支持向量機的量化擇時策略及實證研究[D].西安工業(yè)大學，2017.

[16]Fama，E F.The Behavior of Stock Market Prices [J].Journal of Business，1965，38：34-105

[17]Fama E F.Efficient Capital Markets：A Review of Theory and Empirical Work [J].Journal of Finance，1970，25：383-417

[18]趙子銘.上海證券市場有效性的復合分析[J].大眾投資指南，2019（07）：217-220+222.

[19]梁淇俊.基于生存分析的量化投資模型及其策略實現(xiàn)[D].暨南大學，2015.

[20]約翰.莫非.期貨市場技術分析[M].北京：地震出版社，2017：1-530.

作者單位：華南師范大學數(shù)學科學學院