在自然的過程中形成概念

吳玥

數學是思維的體操，而在數學中概念是思維的基本形式，具有確定研究的對象和任務的作用.然而，在傳統的教學中，教師往往根據教材的編排方式，將概念以“一個定義、幾點注意、大量練習”的方式傳授給學生，忽視了概念在學生知識結構中的生成過程，從而給學生理解概念造成了困難.數學概念課的教學應充分體現出概念的產生、發展、提煉的過程.在這一過程中，逐步引導學生在原有的知識基礎上自主生成概念，體會數學的理性，感受數學的文化與背景.下面以方差的教學為例，加以說明.

一、方差的教學設計

方差是一個發生式概念，在學生的原有知識經驗中并沒有與方差相類似的知識可以通過同化形成方差的概念.所以，在方差的教學中，教師要把握住方差概念的關鍵點和疑點，即方差反映的是一組數據的波動情況;為什么要將各數據與平均數的差平方;為什么最后還要取平均數.教師在把握住這些概念的關鍵點和疑點的情況下，通過設置問題情境和問題串，激發學生疑問并逐步引導學生解決問題、生成概念.以下是參考一些老師有關方差的教學實際后寫出的一篇關于方差的教學設計.

1.設置問題情境，激發學生疑問

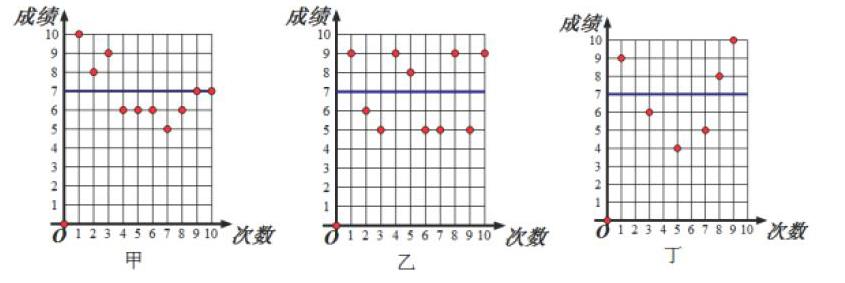
師：甲、乙、丙、丁四名射擊選手的射擊成績如下，請問如果你是教練，你會選誰去參加比賽呢？

生：可以求他們的平均成績，進行比較.

（將學生分為四組，分別求甲乙丙丁的平均成績，學生發現甲乙丁的平均成績相同）

師：甲、乙、丁三人的平均成績相同，那我們該怎么選呢？

生：選成績相對穩定的.

2.引導學生探索，嘗試解決問題

師：我們把甲、乙、丁三個人的成績畫成下面的圖，通過這三個圖，你能發現誰的成績更穩定些？

生：甲.

師：那你能用一個量來刻畫從圖中看出的結果嗎？

生：用每一次的成績與平均成績的差再求和.

師：很好，那大家用這個方法計算一下，看可以嗎？

（學生計算后發現甲乙丁三個均為零）

師：為什么會出現零的情況？

生：因為做差之后出現負數，正負相互抵消了.

師：那怎么避免這種情況呢？

生：可以取絕對值，然后再求和.

……

師：對，像求平均差一樣最后求平均數，現在大家算一下甲、乙、丁最后的結果分別是多少呢？

生：甲、乙、丁計算之后的結果分別是2.2，3.4和 ，結果越小成績越穩定，所以甲的成績穩定，應該選甲去參加比賽.

在教學的過程中，教師要讓學生展示自己的思維過程，從而了解學生的思維方式和思維習慣，弄清學生在解決問題的過程中所遇到的思維障礙.這樣就能更有針對性的對學生進行啟發引導.

本節課在學生的原有知識基礎上，在教師的逐步引導下，學生知道了為什么要引入方差，方差的作用是什么，在計算方差的過程中為什么每個數據要與平均數作差，為什么對差求平方會比取絕對值更好一些，為什么對差求平方后要求平均數.在這些疑點都一一解決后，方差的概念也就清晰了.同時，在這個過程中，學生通過教師的引導不僅能夠更加輕松自然的掌握方差的概念和方差公式，還體驗了探究解決問題的過程和方差的概念的發生、發展、提煉的過程，在這一過程中也體會了數學從特殊到一般的思想.

二、課后感悟

一堂概念課的教學過程，就好像是一個造橋過河的過程.在課程開始時，我們在河的一岸，我們的目的是到達這條河的另一岸，也就是最終生成一個明確的概念.然而，教師不能生搬來一座橋架在河的兩岸，也不能帶著學生直接“飛”到對岸.教師要做的是引導學生發現這條河中可以建造橋墩的地方，并在這里建好橋墩，這個在河中找地方并建橋墩的過程也就是學生探索、起疑并解疑的過程，這在學生自主生成概念的過程中是至關重要的.因此，也要求教師在備課的過程中要精確細致的理解、分析概念，分析學生可能會產生疑問的地方，把握住概念的關鍵點和疑點.這樣才能引導學生一步步的在河中修建好橋墩，橋墩建好了那橋也會相對輕松容易的建好，那學生就能夠通往彼岸.這樣學生也就在一個自然而然的過程中形成了概念.

三、簡要結語

概念的教學過程看似一波三折，但這就是一個概念產生、發展、提煉的過程，是符合學生的認知規律的.教師要善于利用教材，要用活教材，不拘泥于教材，仔細分析教材的編排思路和所教知識的背景、關鍵點和學生的疑點，通過逐步引導，使學生體驗知識的生成過程，讓概念在學生的探究活動中，自然而然的生成.雖然過程看似繁雜，但卻是自然形成的，是符合事物發展規律和思維規律的，數學概念就是自然形成的，數學就是自然而然的.