深圳經濟特區40年經濟增長回顧與展望

董曉遠

深圳經濟特區建立40年來，深圳本地生產總值（GDP）由1979年的1.96億元增長到2019年的2.69萬億元，名義增長1.37萬倍，實際增長2467倍，年均實際增長21.6%，創造了世界城市化歷史上的奇跡。這樣的奇跡，舉世矚目，激發了無數學人的思考：深圳是怎么做到的？成功的經驗與原因究竟是什么？如何總結經驗，繼往開來，在建設中國特色社會主義先行示范區的征程中，續寫輝煌？

一、分析總結深圳發展經驗的多個角度

深圳經濟特區建立40年來的發展，既是從計劃經濟走向市場經濟的改革與轉軌過程，又是融入全球產業鏈的開放過程，也是資本、勞動等要素不斷集聚的工業化和城市化過程。多年來，在深圳發展的各個時期，關于深圳的發展經驗，不同的研究人員，依據不同的研究目的，采用不同的研究方法與角度，得出的結論側重點就會有所不同。正所謂“橫看成嶺側成峰，遠近高低各不同”。

有的研究團隊立足于“觀念是行動的先導”，以思想解放、觀念轉變為邏輯起點，高度評價“時間就是金錢、效率就是生命”“空談誤國、實干興邦”“敢闖敢試、敢為天下先”“鼓勵創新、寬容失敗”等思想觀念對深圳發展的推動作用，認為思想解放是深圳持續發展的原動力。正如有學者指出的：改革開放 40 余年深圳所取得的成就，說到底不是單純資源的勝利與資本、技術的勝利，而是觀念的勝利與制度的力量。①《發揮制度“先行”優勢，理性應對疫情挑戰》，《深圳特區報》2020 年5月26日第 B04 版。有的學者以制度創新為重點，總結深圳的發展經驗，認為：深圳經濟社會面貌發生巨大變化的根本原因在于改革開放。②鐘堅：《深圳經濟特區改革開放的歷史進程與經驗啟示》，《中國經濟特區研究》2008年第1期。中國改革開放后最大的制度創新就在于對經濟特區的特殊政策：一是產權保護和放開投資領域；二是特殊的稅收優惠政策；三是擴大特區政府管理權能。①南嶺：《深圳基因：市場經濟體制形成之初》，《特區實踐與理論》2019年第3期。這是促進深圳經濟發展的重要制度保障，1992年賦予深圳特區立法權，成為深圳繼續發展的重要制度供給。②李東泉、朱祁連：《深圳特區制度的歷史實證分析及未來展望》，《城市觀察》2012年第1期。有的研究團隊以新結構主義經濟學提出的“有為的政府，有效的市場”為主線，總結40年來深圳市委市政府在培育和引導市場發展方面做了哪些工作、出臺了哪些政策，使得深圳的生產資料市場、勞動力市場、金融市場等不斷發育完善，高效運轉，從而促進了深圳經濟的高速發展。有的學者高度重視區位優勢的作用，認為廣東哪個地方離香港的距離越近， 哪里的經濟發展就比較快， 相反則相對落后。與香港一河之隔，正是深圳經濟特區在五個特區中發展最快的一個重要因素。③羅木生：《區位優勢對經濟特區發展的影響》，《特區經濟》1995年第2期。有的學者利用新古典經濟學的生產函數模型，從資本積累、勞動力增加與技術進步的角度來分析深圳的經濟增長。④褚可邑：《運用生產函數模型分析深圳經濟的增長》，《深圳大學學報（人文社會科學版）》1998年第1期。有的學者根據古典經濟學關于勞動分工是經濟發展和增長的原動力的理論，擴展了新興古典經濟學關于內生專業化勞動力增長的模型， 以此來解釋深圳持續跨越式的產業升級和趕超型增長。⑤唐杰等：《深圳經濟增長的理論研究》，《中國經濟特區研究》2010年第1期。

以上各種觀點的主要區別，在于邏輯起點的不同，在于看問題的角度或強調重點的不同。對于深圳的經濟發展實際上是由多種因素共同推動，大家是沒有異議的。難點在于判斷哪種因素在什么時間起了多大作用，“可復制、可推廣”的經驗究竟有哪些。

生產函數模型依然是當今分析經濟長期增長的主流方法。預測未來的經濟增長，需要確定哪些因素會影響未來的經濟增長以及這些因素如何影響經濟增長。預測的邏輯框架，是歷史經驗與規律的高度提煉與概括。他山之石，可以攻玉。雖然發達國家眾多的經濟學家通常不會對深圳的經濟增長進行系統分析，但他們對自己國家經濟潛在增長率⑥所謂經濟潛在增長率，是指一個經濟體在充分利用產能和充分就業的情況下所能維持的增長率。潛在產出不是無法超過的產出上限。相反，它衡量的是最大可持續產出，是通脹穩定年份的實際產出（GDP）水平。的分析方法，卻給我們回顧深圳經濟發展提供了方法論的啟示。發達國家的一些著名研究機構在分析本國潛在產出時，大多采用生產函數法，如國際貨幣基金組織（IMF）、經合組織（OECD）、美國國會預算辦公室（CBO）、歐盟獨立財政機構（IFIs：independent fiscal institutions）等。自從1995年10月發布《國會預算辦公室測算潛在產出方法的備忘錄》以來，美國國會預算辦公室一直使用新古典增長模型的框架來估計潛在產出的歷史數據并預測其未來數值。增長模型使用新古典生產函數，結合關于勞動力增長和儲蓄率（投資率）的假設，來確定長期產出如何增長。20多年來，盡管在一些變量測算及其趨勢預測的細節上做出許多改進，但新古典主義的生產函數的基本框架一直沒變。美國國會預算辦公室的索洛模型采用了科布—道格拉斯生產函數的形式：⑦Robert Shackleton：Estimating and Projecting Potential Output Using CBO’s Forecasting Growth Model，美國國會辦公室工作論文，2018年2月。

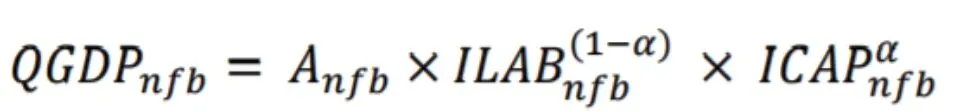
其中，QGDPnfb為非農業部門（工商部門）的實際GDP；Anfb為該部門的全要素生產率指數，ILABnfb為該部門的勞動工時指數，ICAPnfb為該部門的資本服務指數；α為該部門生產過程中資本的相對貢獻。

歐盟獨立財政機構（IFIs）的大多數成員（包括歐盟委員會、國際貨幣基金組織、經合組織、財政部、中央銀行、國家統計局等15家單位），估計潛在產出時，用得最多的方法是生產函數法，其次是霍德瑞克—普雷斯科特（HP）濾波法。國內外多家機構曾運用生產函數法對中國經濟潛在增長率進行估算。可見，盡管學術界有新經濟增長理論等一些理論與方法的創新，但新古典的生產函數模型在實踐中依然是有效且被廣泛采用的。

二、新古典生產函數模型能解釋99%以上的深圳人均GDP① 人均GDP通常是GDP除以常住人口。這里所說的人均GDP指的是GDP除以從業人員數（勞動力人數），嚴格說來應該稱為勞均GDP（勞動生產率）。勞動力只是常住人口的一部分。但勞均GDP及勞均資本裝備，總沒有人均GDP、人均資本裝備朗朗上口，為免歧義，特此說明。增長

（一）深圳經濟增長的歷史數據，有明顯的規律

根據生產函數理論，在規模報酬不變的條件下，人均GDP與人均資本裝備成對數線性關系。我們將深圳40年來的實際人均GDP與人均資本裝備的對數制成散點圖，發現深圳的數據，非常符合理論預期（見圖1）。

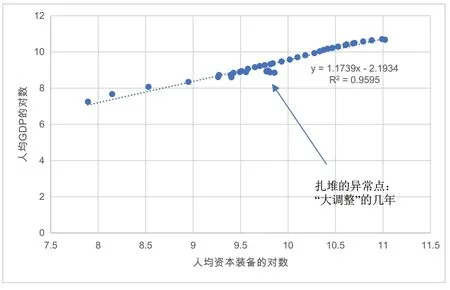
圖1 深圳人均GDP與人均資本裝備成對數線性關系

圖1 中的幾個異常點，反映了深圳經濟發展史上脫離常軌的一段“大調整”。1986年，深圳對全市1500多項基建項目進行了全面清理，基建規模壓縮一半以上，施工隊伍裁減近10萬人，20層以上的高樓停建了60多棟。②https://www.sohu.com/a/247644852_780216.經過調整，深圳的經濟開始進入正常軌道，再未出現過大的起伏（見圖2）。

（二）新古典生產函數模型及其估計

1.模型設定。典型的柯布—道格拉斯生產函數由三個因素組成:勞動力，資本和生產率。標準公式是（未考慮技術進步）：Y=AKαLβ

其中Y為國內生產總值，K為資本存量，L為就業人數，α為資本的產出彈性，β為勞動的產出彈性（α與β為待估參數），A為常數，代表技術水平。

考慮了技術進步的生產函數：Y=(AeYt) KαLβ

其中Y為技術進步率，t為時間，其余變量意義與前式相同。

假設規模報酬不變，即α+β=1，于是上述兩個生產函數可分別進一步簡化為如下形式：

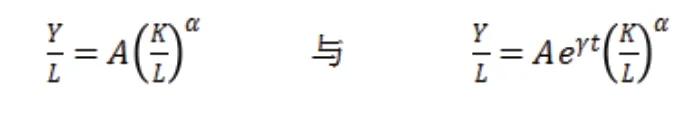
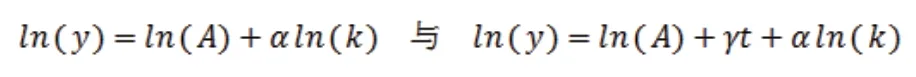
使用深圳歷年相應數據分別對上面兩個對數線性方程進行回歸，就可以估計出資本的產出彈性α，勞動的產出彈性β，（初始）技術水平A；根據后面一個方程還可以估計出全要素生產率的變化率γ。

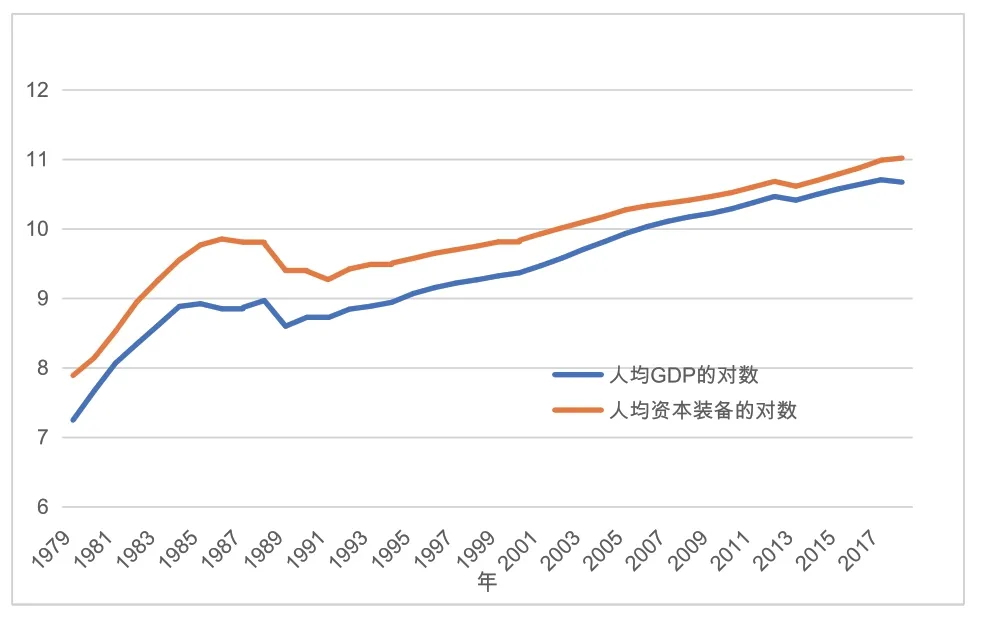
圖2 大調整之后深圳進入正常發展軌道

2.深圳實際GDP與GDP平減指數測算。根據《深圳統計年鑒2019》公布的深圳各年GDP及其增速，深圳實際GDP與GDP平減指數測算結果如表1：

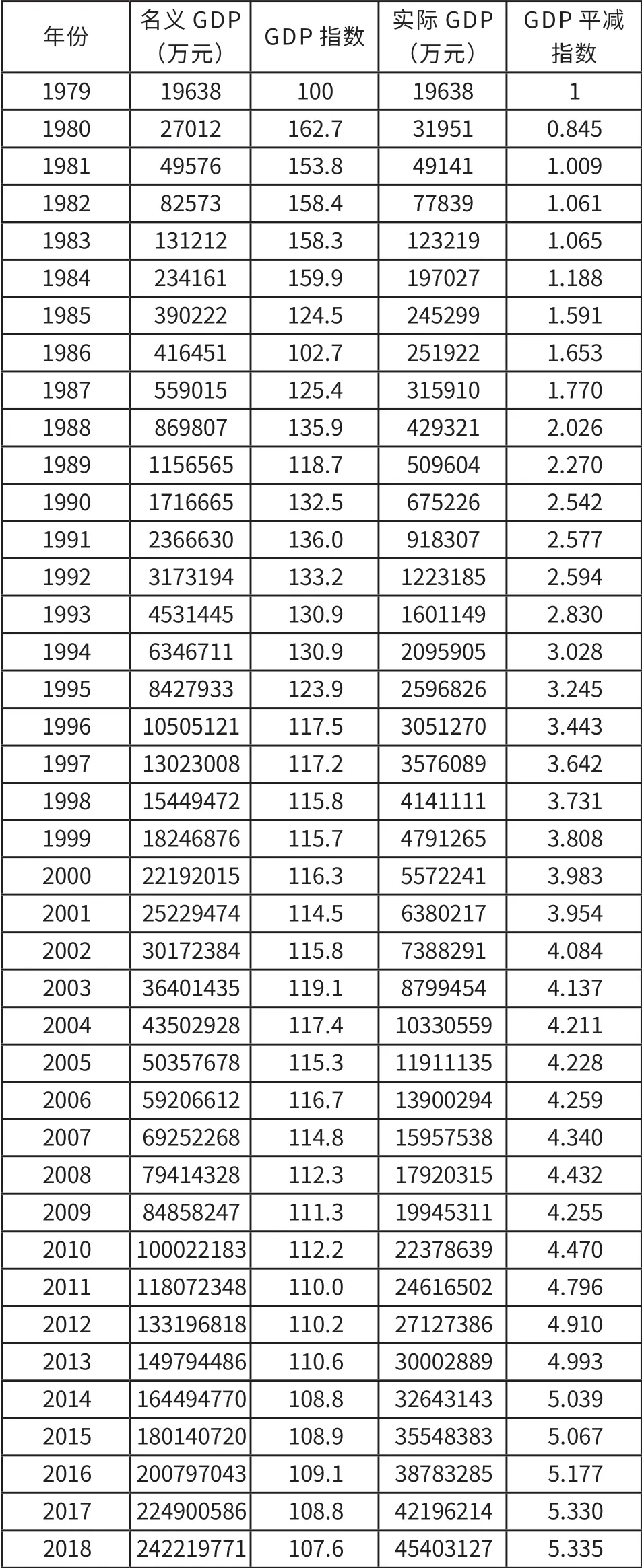
表1 深圳實際GDP與GDP平減指數測算結果

3.勞動力人數。勞動力人數的數值采用了深圳統計年鑒公布的歷年深圳就業人數。

4.深圳資本存量的測算。測算資本存量的基本方法是Goldsmith于1951年開創的永續盤存法，現在被OECD國家廣泛采用。

基本公式為：Kt=It+(1-δt)Kt-1

其中，Kt為第t年的資本存量，It表示第t年的投資，δt表示第t年的折舊率。要測算深圳的資本存量K，有四個關鍵：基年資本存量、固定資產投資價格指數、當年投資和折舊率的確定。

關于深圳的資本存量數據，統計部門沒有公布，只能根據永續盤存法利用歷年固定資產投資數據來推算。本文計算深圳資本存量時所用的基年，定為1979年。基年資本存量，根據增量資本產出比（ICOR）①增量資本產出比（ICOR） 即資本存量變動與產出增量 （△GDP） 的比率，當不考慮固定資產折舊時，資本存量的變動等于投資流量I，即資本形成總額，所以，ICOR =I/△GDP 。與深圳當年的GDP推算。深圳經濟特區成立之初五年的資本產出比的平均值約為1.91。關于深圳的固定資產投資價格指數，沒有現成統計數據可用，暫用深圳的GDP平減指數②GDP平減指數等于現價GDP除以不變價GDP（實際GDP）。例如，若1978年的指數為100，1979年的GDP指數為107.6，是指與1978年相比，按可比價計算，GDP增加了7.6%；若1978年的GDP為3624.1，則按不變價計算，1979年的GDP等于3624.1乘以107.6等于3899.53，則1979年的平減指數為現價（1979）4038.2/3264.1=103.56，據此計算GDP平減指數。替代。在計算深圳的固定資產投資時，我們采用全社會固定資產投資這一口徑，但要經過投資價格指數換算為1979年不變價。許多研究都把資本存量折舊率定為6%左右，我們暫取6%進行測算。資本存量的測算結果見表2。

5.模型估計結果。根據1979年以來深圳的實際GDP、資本存量、就業人數對帶有時間t的生產函數進行回歸，測算結果見表3—表5。可見，模型估計結果相當良好。變量系數符號合乎理論預期，各項估計都輕松通過顯著性檢驗。由此得出深圳的生產函數：

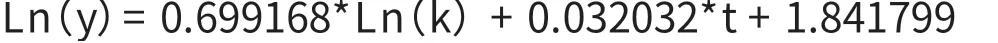
測算結果表明，在觀測期內，深圳的人均GDP變化的99%以上，都可以用人均資本裝備水平和技術進步（全要素生產率）來解釋。

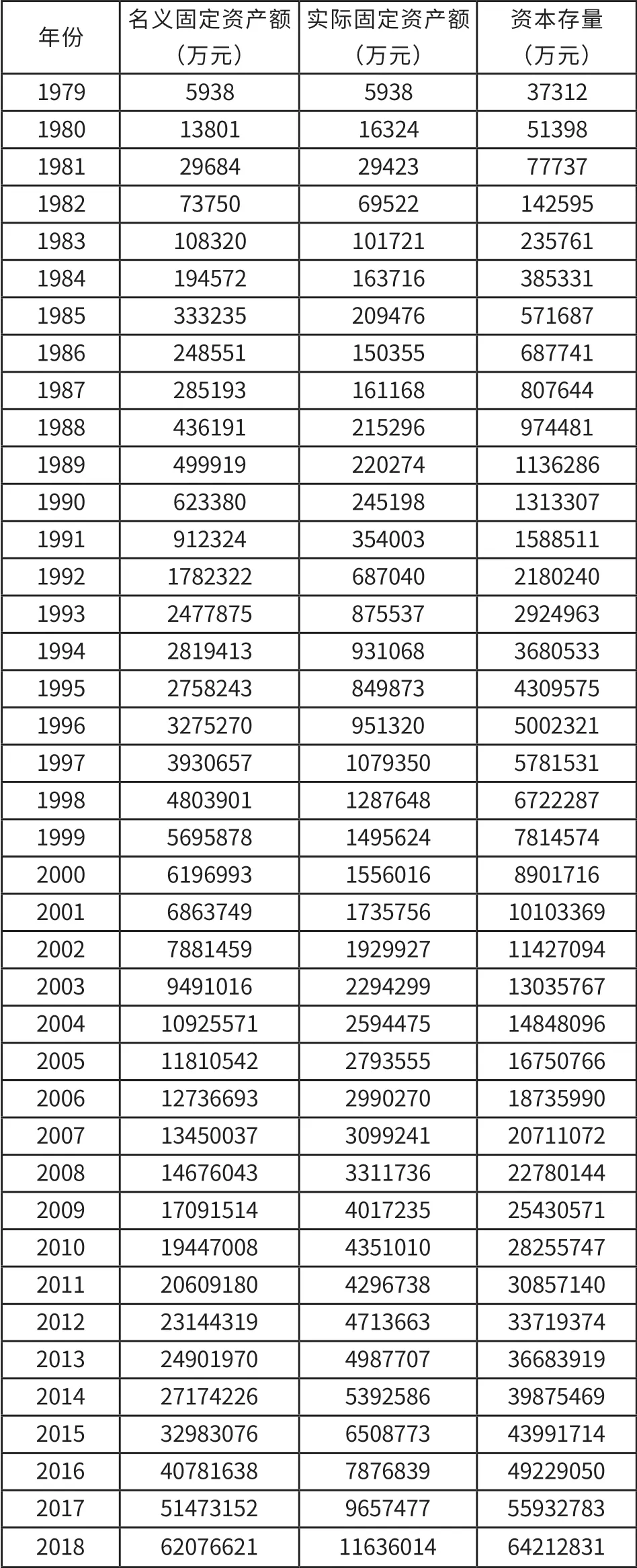
表2 資本存量的測算結果

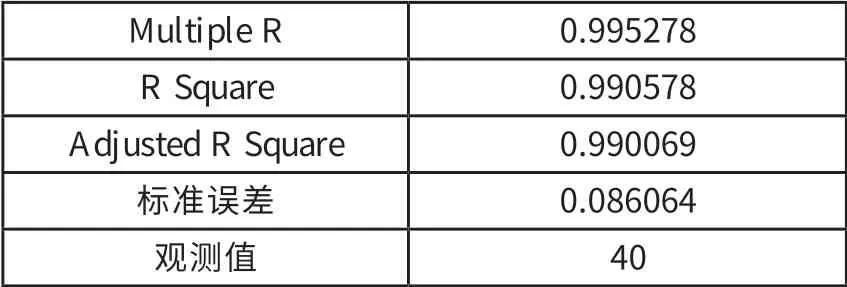
表3 回歸統計

表4 方差分析

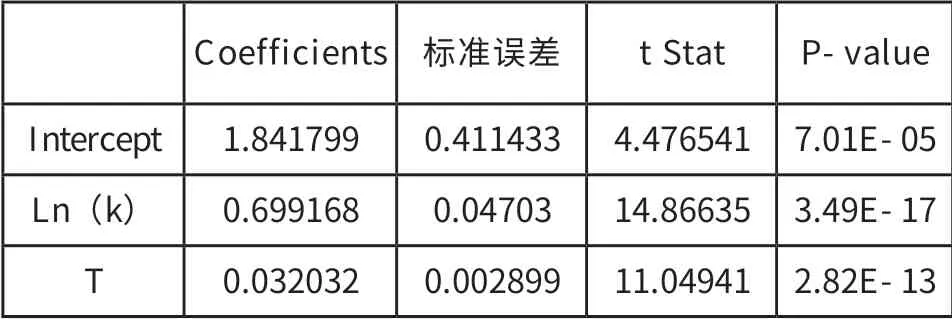
表5 參數估計

（三）生產函數模型估計結果的討論

1. 資本積累、勞動力增加與技術進步三大變量，能夠很好地解釋40年來深圳的經濟增長。將前面估計的人均產出、人均資本裝備形式的生產函數還原為柯布—道格拉斯生產函數的形式，即：

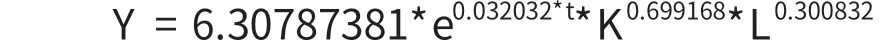
這一生產函數表明，從40年來深圳發展的歷程看，深圳的資本存量每增加1%，深圳的實際GDP就增長約0.7%；深圳的勞動力每增加1%，深圳的實際GDP就增長約0.3%；深圳的全要素生產率平均每年提高3.2%。

新古典生產函數對深圳經濟增長的解釋力相當強。用資本積累、勞動力增加與技術進步（全要素生產率）這三個變量，就能夠很好地解釋與擬合近40年來深圳的經濟增長（見圖3）。

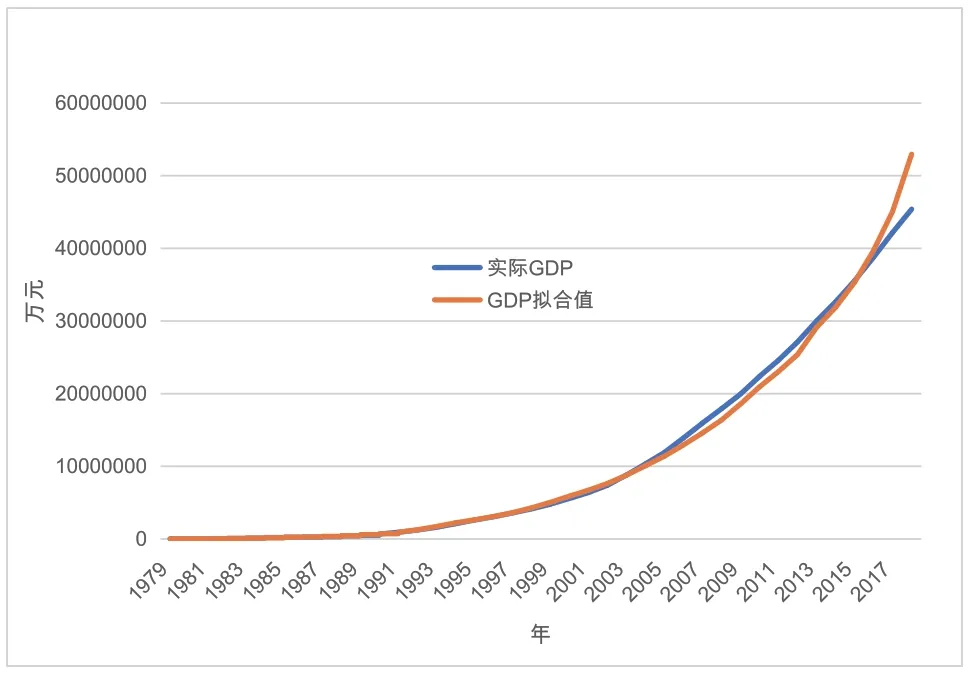
圖3 深圳實際GDP及其擬合值

從圖3可以看出，近幾年深圳的實際GDP明顯低于模型擬合值，即同樣多的資本積累與勞動力增加，GDP沒有達到應有的水平。這很可能是由以下原因引起的：一是投資結構不合理。總量生產函數不討論結構問題，但它以結構合理為前提。如果投資結構不合理，投資不足的部門很可能形成瓶頸，制約經濟的發展。舉一個簡單的例子，假定在運輸部門已經滿負荷運轉的情況下新增投資全部集中于工業生產部門，使得生成能力成倍增長，但貨物運輸能力沒有提高，必然導致所需的原材料不能及時運進來、制成品無法及時運出去，新形成的產能不得不“等米下鍋”，投資就達不到應有的效率。反過來，如果投資全部集中于運輸部門，使得運輸能力成倍提高，但工業部門產能沒有相應擴大，就會造成運輸能力的閑置與浪費，投資也達不到應有的效率。合理的投資結構是按比例擴大生產能力與運輸能力，使之達到滿負荷運轉，這樣，投資才能達到應有的效率與產出水平。二是全要素生產率沒有按照以往的年平均增速勻速提高。中美貿易摩擦，使得深圳引進消化吸收國際先進技術的難度增加，技術進步變慢，全要素生產率無法像貿易摩擦之前那樣勻速提高。三是隨著居民生活水平的提高，對環境質量要求也越來越高，固定資產投資中用于環境保護和環境改善的投資（如污臭河道整治、道路綠化美化）逐漸加大。而環保投資與工商業投資相比，不能或只能產生較少的GDP。實際情況，或許是以上幾種因素兼而有之。

2.新古典生產函數模型，考慮了經濟增長所有的相關因素，包容力強。新古典生產函數模型，將經濟增長的核心要素歸結為三個方面，一是資本積累，二是勞動力增加，三是除了上述兩大因素之外的所有其他因素，稱為“索洛剩余”，即所謂的技術進步或全要素生產率。制度經濟學的研究表明，好的制度，通過對權利、義務、責任和程序的有效安排，可以降低交易成本，提高生產效率。制度變遷、制度完善帶來的生產效率提高，會在全要素生產率中體現出來。思想解放、觀念變革引起制度創新，從而帶來的效率提高，也會體現在全要素生產率的提高上。

3.制度對經濟增長的促進作用，是通過要素積累與效率提高實現的。新制度經濟學認為，世界上大部分的經濟是不發達的，原因就在于它們的制度阻礙了自己的發展。深圳之所以取得了發展的輝煌成就，就在于依靠改革打破了制約發展的制度障礙，這是學界與政界的共識。

根據我們按照新古典經濟學框架進行的研究，深圳人均GDP增長的99%以上，可以由資本積累、勞動力增加和技術進步三個因素來解釋。但要進一步追尋原因：資本、勞動和技術為什么會集聚于深圳？這涉及制度變遷和制度創新。深圳經濟特區建立以來，進行了一系列卓有成效的制度改革，如：在當時內地企業按55%的累進稅率納稅的情況下，將深圳經濟特區的企業所得稅降為15%。大幅度的稅率優惠，吸引了國內外資本紛紛進入特區；在勞動用工制度方面率先打破“大鍋飯”，實行超產獎勵制度，勞動者的收入大幅提高，吸引了大批勞動者源源不斷地流入深圳；1987年出臺的《關于鼓勵科技人員興辦民間科技企業的暫行規定》，點燃了無數懷揣夢想的科技人員的創業激情，大量科技人員紛紛來到深圳創業，大大促進了深圳的技術進步。

由此可見，沒有制度創新，就沒有勞動、資本和技術在深圳的積聚，就沒有深圳經濟的高速增長。從這個意義上講，制度變遷是深圳經濟發展的第一推動力。各種因素對經濟增長的促進作用（見圖4）。

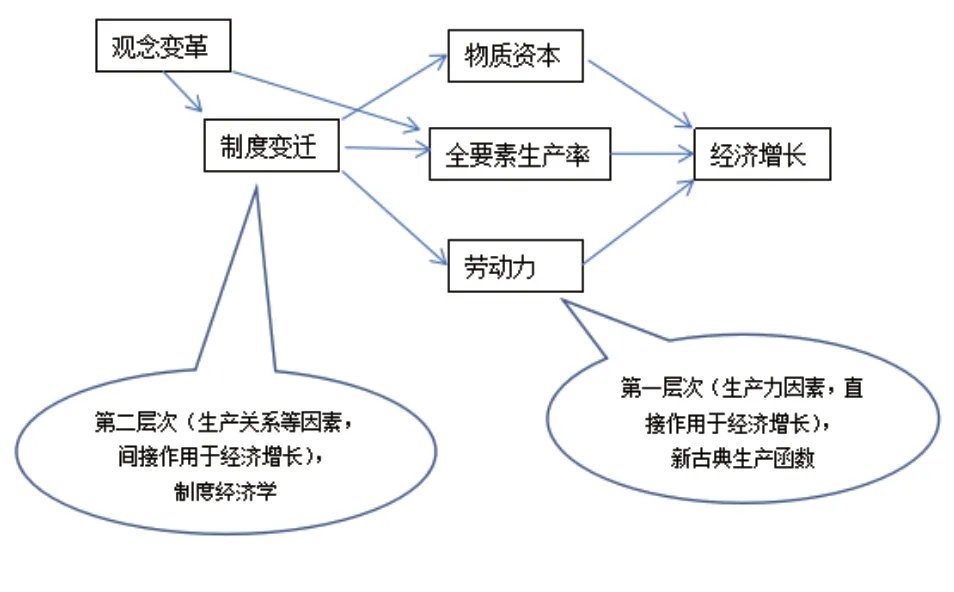
圖4 各種因素對經濟增長的促進作用

當然，也不能認為觀念變革就是終極原因、是深圳發展的“第一推動力”。它只是多種因素相互作用的一個環節。馬克思主義認為：社會歷史的發展與變遷是很多因素共同作用的結果，但在諸多因素中“歸根結底”的原因只能是經濟因素。

從方法論的角度講，作為回顧深圳發展歷程有用的定量分析工具，可計算一般均衡模型已經能夠系統地分析經濟增長的主要因素。可計算一般均衡模型將宏觀總量的生產函數應用到各個行業各個部門，能夠同時考慮總量與結構問題。它將稅率與工資水平分別納入價格方程與勞動力供求方程，可以較好地模擬稅收政策、工資政策等變動帶來的影響。它通過引力方程把貿易流量、運輸費用和空間距離聯系起來，因而也能夠分析區位優勢的問題。但可計算一般均衡模型通常規模龐大、操作復雜，如中國社科院與澳大利亞莫納什大學政策研究中心合作開發的PRCGEM模型，包括118個部門、30個地區，186類共近萬個方程，250類數十萬個變量。①鄭玉歆、樊明太等：《中國CGE模型及政策分析》，北京：社會科學文獻出版社，1999年。相比之下，新古典生產函數，僅用幾個變量就解釋了GDP的絕大部分變化。

三、深圳“十四五”經濟增長展望

新古典生產函數不僅可以用于回顧歷史，還可以用于預測未來的經濟增長。預測未來五年深圳的經濟增長，必須對未來資本存量、社會勞動者人數做出預測。深圳是一個移民城市，勞動力的流入和流出與工作機會高度相關。可以認為：如果深圳的資本投入增長，總可以獲得足夠的勞動力來推動這些資本的運用；深圳經濟增長主要取決于資本投入的增長，勞動投入的增長只是資本投入增長的結果而不是推動增長的原因，而且相當大部分的技術進步會體現在新設備的高效率上。從這個意義上說，深圳的經濟增長，主要取決于資本投入的增加。

（一）“十四五”期間深圳GDP的年均增長率，取決于未來五年的總投資規模

人均資本裝備水平不斷提高，新增等量資本所需追加的勞動力越來越少。深圳資本與勞動的關系，或者說資本對勞動的需求，可以用人均資本裝備來表示。近三十年來，隨著技術的不斷進步，深圳的人均資本裝備水平也不斷提高，詳情見圖5。

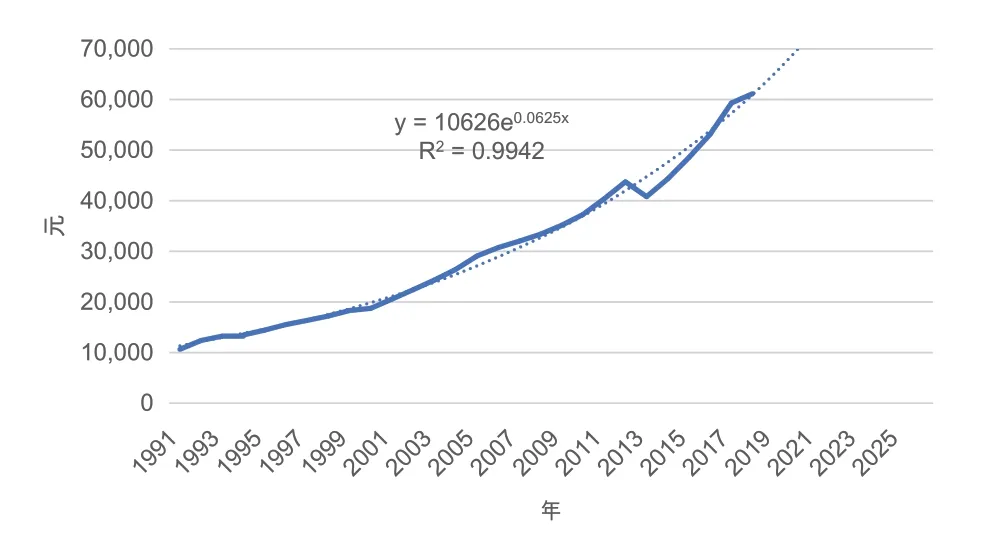
圖5 深圳人均資本裝備及其變動趨勢

深圳未來五年的年均經濟增長率與這一時期的固定資產總投資規模成線性關系。對于深圳未來五年的固定資產投資，我們大致按高、中、低三種方案進行預測。其中，高增長方案假設深圳在“十四五”期間的固定資產投資額，依然夠沿著近幾年來形成的二次曲線趨勢增長，低增長方案假設深圳在“十四五”期間的固定資產投資額，將按近幾年來形成的線性趨勢增長；中增長方案則取二次曲線與線性預測的平均值。二次趨勢線揭示了正常情況下深圳“十四五”期間投資增長的可能性，我們還可以根據線性增長趨勢對深圳“十四五”期間的投資增長進行模擬預測，結果見圖6。

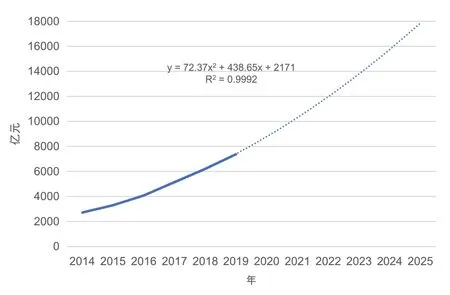
圖6 深圳名義固定資產額擬合與預測

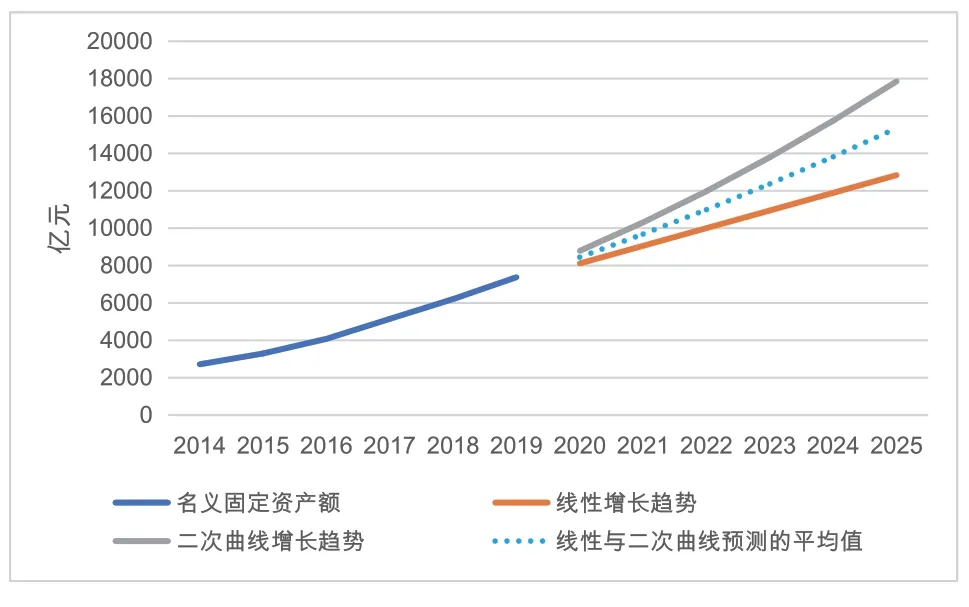
圖7 深圳固定資產投資預測

如果“十四五”期間，深圳的固定資產投資能夠沿著近些年形成的二次曲線趨勢穩步增長，那么，2021-2025年深圳的名義固定資產投資額將分別達到10312億元、11981億元、13795億元、15753億元、17856億元，即五年總投資達到69697億元。將預計的“十四五”期間名義投資額折算為實際值再代入資本存量計算方程，可得2021—2025年資本存量估計值。2021—2025年深圳就業人員數，可以用資本存量除以當年的人均資本裝備求得。將“十四五”期間各年的資本存量與就業人員數代入深圳的生產函數，即可以求得各年GDP及其增長率。考慮到近年來國際經貿環境的“百年未見之大變局”會深刻影響經濟增長的軌跡，使得模型預測值出現系統性偏差，必須根據偏離情況，乘以一個適當的比例修正系數，才能得到較為符合實際的預測值。詳情見表6：

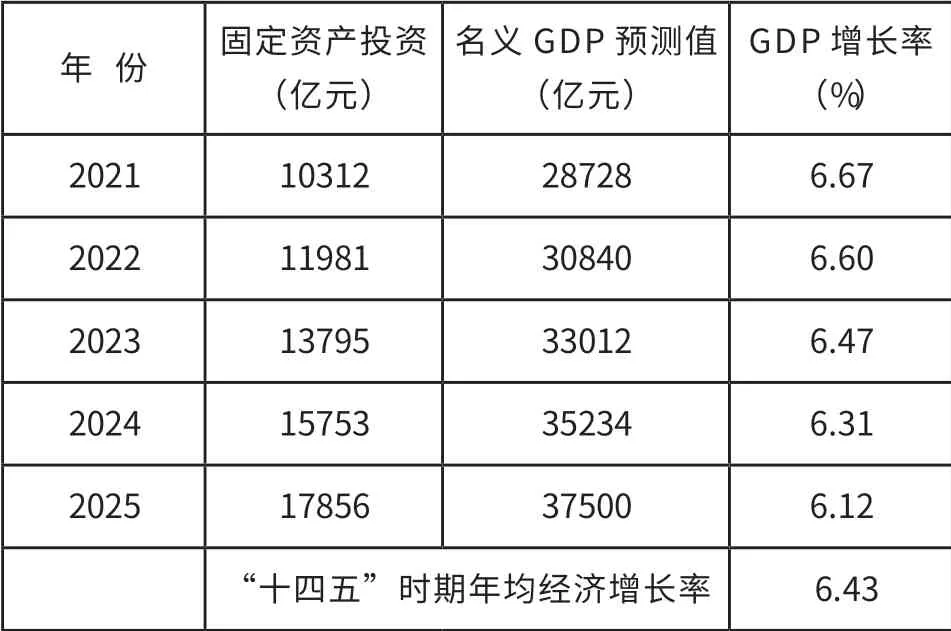
表6 “十四五”期間深圳的固定資產投資與 GDP增長率預測

按照同樣的方法與步驟對中與低方案的固定資產投資額與相應的GDP增長率進行預測，所得結果如表7：

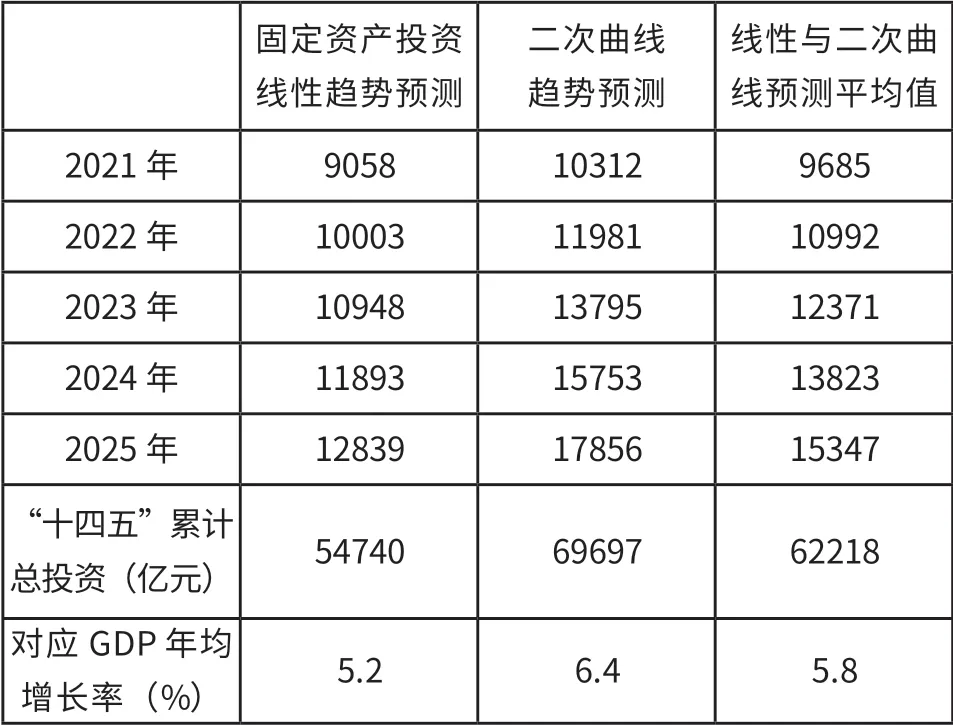
表7 深圳“十四五”固定資產投資及相應的GDP增長預測

將表7以及其他幾種可能的“十四五”期間固定資產累計投資總額與相應的GDP增長率合在一起制成一張散點圖，可以觀測到兩者之間的關系，見圖8：

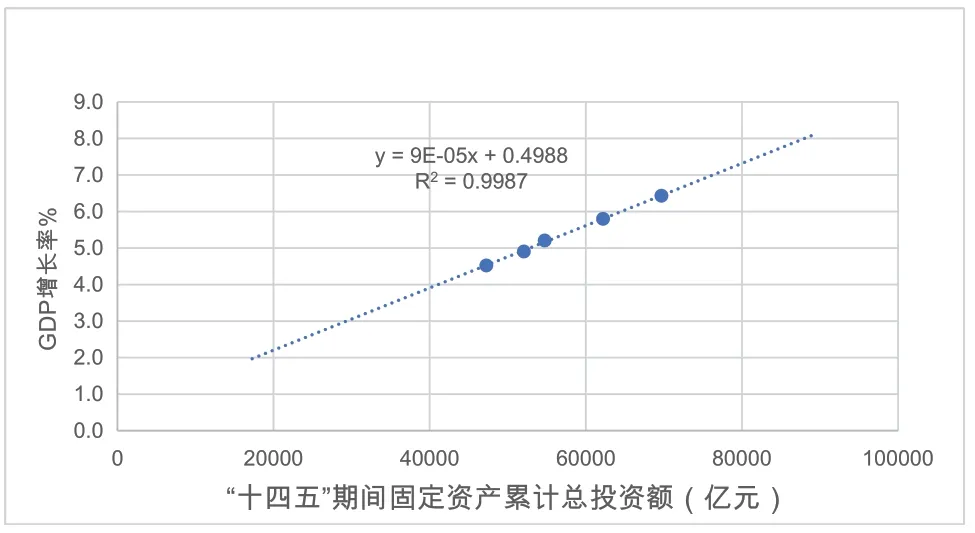
圖8 深圳市“十四五”期間固定資產累計總投資額與相應GDP年均增長率的關系

可見，“十四五”期間，深圳固定資產投資總額與年均GDP增長率之間，呈現出一種近乎完美的線性關系：固定資產投資總額每增加1萬億元，其年均GDP增長率就能夠提高0.85個百分點。“十四五”期間深圳各種可能的固定資產投資總額及其對應的GDP增長率，都可以根據圖7顯示的線性關系推算出來。這一線性關系的成立，不是偶然的。

由上述線性關系，可以推論：如果“十四五”期間深圳固定資產投資總額能夠確保達到65000億元以上，那么實現6%的GDP年均增長率就是有保障的；如果同期的固定資產投資總額能夠達到69697億元，那么實現6.4%的GDP年均增長率是很有希望的；如果未來五年深圳難以找到足夠多的投資項目，企業投資信心不足，致使完成47262億元的固定資產總投資額都有很大難度，那么，深圳“十四五”期間的增長率將不足5.2%。

上述分析，考慮了固定資產折舊，但沒有考慮企業外遷造成的資本存量下降。如果將企業外遷造成的資本存量減少代入模型測算，GDP增長率還會相應下降。另外，上面的分析，仍然假定深圳的技術進步會按過去的速度勻速前進，主要基于以下考慮：雖然未來幾年引進消化美國先進技術的難度加大了，但深圳可以更多地引進其它國家的先進技術，同時，深圳的研發投入將持續加大，總起來看，技術進步的速度或許不至于有顯著差異。

（二）深圳固定資產投資總額與年均GDP增長率之間的線性關系，有較強的決策參考意義

如上所述，經過復雜的推導和計算，最后，我們發現了一個十分簡潔明快的經濟關系，即：深圳市“十四五”期間的年均經濟增長率，與規劃期間全社會固定資產投資累計總額之間，呈十分明顯的線性關系。這一線性關系，這不是數據巧合，是有著內存聯系的一種較為穩定關系，因而具有較強的決策參考意義。

我們知道，柯布—道格拉斯的生產函數 ，①下面大寫字母表示經濟變量，小寫字母表示相應變量的增長率。寫成增長率形式，為：y = a + α*k + β*l

在通常的規模報酬不變的假設下，有 α + β = 1

于是，增長率方程變為：y = a + α*k +（1-α）*l

令資本折舊率為δ，根據資本存量的永續盤存法計算公式，資本存量的增長率k，可以寫為：k =（Kt- Kt-1）/Kt-1= It / Kt-1- δ = - δ +（1 / Kt-1）*It

由于Kt-1是上一年的資本存量，是一個既定數值，（1 / Kt-1）是一個常數系數，（-δ）是上面一元線性方程的截距項，因此，資本存量增長率與當年投資額的大小呈嚴格的線性關系。

在技術水平不變的條件下，體現著技術水平的人均資本裝備水平不隨著固定資產投資總額的變化而變化。②當然，如果新增投資總是用于購買最新最先進的設備，從而使得全社會先進設備的擁有量隨投資額而增大，技術不變的假設就會遭到破壞，這時全社會的技術水平會隨著投資的擴大而提高。在勞動力充分供給的條件下，資本存量變化會引起勞動力同比例變化。于是：

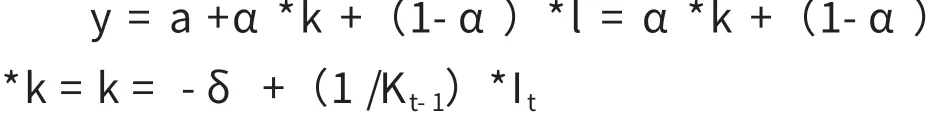
在這種情況下，生產函數中資本的產出彈性α與表示勞動的產出彈性β的具體數值已經不重要了，因為它們在增長率公式中已經消失了。

當人均資本裝備水平隨著新增資本存量規模而變動時，資本或勞動的產出彈性值的重要性就顯現出來了。這時，有：

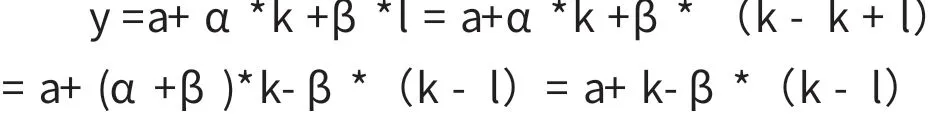
其中，（k - l）正是勞均資本裝備水平的變化率。由于勞動的產出彈性β為常數，如果人均資本裝備水平的變化率（k - l）不變，那么，-β*（k - l）就是一個常數；如果a再為常數（即a表示年平均技術進步速度或平均的全要素生產率變化，本文中正是這樣定義的），那么，GDP增長率仍然與資本存量從而與固定資產投資額成嚴格的線性關系。如果（k - l）不再保持不變，但變化幅度較小，接近于常數，那么，GDP增長率y與固定資產投資額成近似線性關系，各散點會分布在直線附近。從深圳的實際數據來看，勞均資本裝備水平的變化率自1995年以來，走勢較為平穩，變化幅度比較小。

如果每一年的GDP增長率都與固定資產投資額成嚴格線性關系，那么，五年經濟增長率的平均值（約等于各年經濟增長率的算術平均值），在（1 / Kt-1）很小且變化不急劇的情況下，可令各年的（1 / Kt-1）約等于一個常數，因此，各年經濟增長率的平均值就與各年固定資產投資的累計額成不十分嚴格的線性關系。于是，我們就看到了五年經濟增長率平均值與五年固定資產投資總額散點圖呈明顯的線性關系。

因此，我們通過復雜計算得出的關于“十四五”期間年均經濟增長率與固定資產投資總額的線性關系，不是數據巧合，而是具有相當的普遍性。

當然，還應強調，這一線性關系的成立，應該以投資結構的合理為前提，以投資的有效性為前提。順便指出，資本積累的重要性，以創新為研究重點的“新經濟增長理論”也不否認。“新經濟增長理論”認為，資本的貢獻要大于傳統增長模型刻畫的貢獻，因為增加的資本不僅通過其對生產的直接貢獻來提高產量，而且通過“干中學”等間接推動新思想的發展來提高產量。資本不僅包含物質資本，而且也包含人力資本，因而資本仍然是增長問題的關鍵。存在著投資（即資本的積累）刺激知識的積累，反過來知識的積累又促進投資的良性循環。

總的來說，一定規模的投資，是推動經濟特區持續快速發展的重要支撐。受新冠肺炎疫情影響，全球正在經歷一場前所未有的危機，國際貨幣基金組織最近預計2020年全球經濟增長率將下降4.9%，同時預計中國2020年經濟增速為1%，為全球主要經濟體中唯一增長的國家；2021年中國經濟增長將達到8.2%，是所有國家中增速最高的。對比之下，我們都應該對深圳經濟特區的發展前景有更加堅定的信心。只要政府與民間齊心協力、加大投入，再接再厲，就能夠續寫深圳經濟特區的輝煌。