突發事件沖擊下基于或有支付機制的創投融資決策*
趙林夢,胡支軍
(貴州大學 數學與統計學院,貴州 貴陽 550025)
1 引 言
全球經濟發展的實踐表明, 創新型中小企業是經濟發展的重要推動力量.風險投資作為一種主要以高科技、高風險的創新型項目為投資目標的資本形式, 在幫助創業企業解決融資難等問題上發揮著重要的作用.就創業企業而言,其投資項目的價值除了受市場不確定性的影響外,還會受到突發事件,如自然災害、瘟疫、金融危機、新競爭者的加入等的沖擊.這些突發事件會導致項目的價值發生離散的跳躍.如何測度這些不確定性與特定的跳躍風險對創業企業的價值以及投資閾值的影響,是評估創業投資時的一個重要課題.
從金融學角度看,創業企業融資決策通常涉及對創業企業的估值,創業企業家(EN)和風險投資家(VC)如何分割企業所有權也是其中的相關問題.考慮到創業企業前景的不確定性,EN和VC可以選擇通過預付股權或現金溢價,或者根據企業的業績基準設置一個或有支付機制(Contingent Payment Mechanism,CPM)來解決關于項目估值和企業所有權的問題.或有支付機制(CPM),文獻中也稱為或有Earn-outs, 是在并購交易中買賣雙方為解決估值分歧,依據標的資產未來業績等條件的達標程度來調整支付款項的一項合約安排.在這種支付安排下,并購雙方通過將傳統的一次性支付轉變為延期支付的模式,以解決雙方的估值分歧.
目前關于創業融資決策或者在并購(M&A)環境下涉及CPMs的決策模型的文獻并不多見.Datar等(2001)[1]指出,CPM是一種收購方法,其中賣方收到的最終對價是基于其業務的未來表現.Lukas等(2012)[2]對CPMs采用兩階段期權博弈方法,以考察不確定性和或有支付條款對最佳并購時機的影響.Barbopoulos和Sudarsanam(2012)[3]指出CPM可能出現在“媒體和娛樂”、“消費品”、“高科技”、“醫療”和“電信”等行業.Lukas和Heimann(2014)[4]通過一個具有信息不對稱特征的并購環境下的理論模型,推導出了一系列關于或有支付機制的可檢驗的經驗命題.Choi(2016)[5]針對并購背景建立了一個兩階段博弈模型,目的是解決交易后期如何影響最優或有支付機制的設計問題.謝藹瑩(2018)[6]針對信息不對稱和未來不確定性帶來較大風險的問題,結合相關并購案例研究或有支付可能產生的正面和負面效應.Tavares-G?rtner等(2018)[7]設計了一種實物期權方法對所確定的四種主要不同的CPM進行估值,并展示了如何最優地設計這些不同的CPM,以便在EN和VC之間不會產生利益沖突的情況下,最好地支持創業企業的成長戰略.
隨機過程選擇在實物期權估值中起著核心作用,它不僅會影響項目價值,還會影響投資規則.以往關于創業投資的研究大都是假設項目的投資價值為連續(擴散)隨機過程,投資期間沒有考慮突發事件發生的可能性.例如,Berk等(2004)[8]將未來現金流量風險分成系統風險與技術的特定風險來評估創投的價值與風險溢酬.陽軍等(2012)[9]假設產品需求服從幾何布朗運動,應用實物期權理論方法推導出不變產出和可變產出條件下企業最優投資時機和投資規模的解析表達式.Lukas等(2016)[10]假設項目價值服從幾何布朗運動,基于 EN和VC之間的期權執行博弈提出一個創業融資的動態模型,分析了多階段融資以及經濟和技術不確定性對最優合約的影響.Tavares-G?rtner等(2018)[7]假設創業企業的利潤流服從連續的幾何布朗運動,證明了最優投資時機與CPM的選擇無關.Tavares-G?rtner等(2018)[11]基于EN和VC對創業企業的成長前景持有相同和不同的觀點,建立了一個實物期權模型來確定促使EN和VC同時對創業企業行使增長期權的最優股權結構.Chang等(2020)[12]研究了創業企業的項目價值存在多種可能的概率分布且EN和VC對項目付出的努力具有互補效應時的風險投資最優合約設計問題.
隨著社會、經濟、環境等領域的系統復雜性日益增加,創業企業投資項目的價值除了受不確定性的影響外,還會受到金融危機、自然災害、重大疫情或新競爭者的加入等突發事件的沖擊(穆慶榜(2016)[13]),導致項目價值運動的隨機過程呈現出不規則的離散跳躍,幾何布朗運動等連續型隨機過程并不能完全刻畫項目價值的真實變化情況.因此很有必要在分析中引入“泊松(Poisson)跳躍”過程來模擬這種由突發事件所導致的價值跳躍,更加真實地描述投資項目價值變化的隨機過程,進而克服基于幾何布朗運動等擴散過程的投融資決策的不足.
針對現有基于CPM的創業融資決策模型的不足,拓展Tavares-G?rtner等(2018)[7]的研究,假設創業企業的利潤流服從帶Poisson跳躍的幾何布朗運動,應用實物期權方法研究突發事件影響下創業企業的最優融資決策問題,設計最優的或有支付機制就很有必要了.
2 突發事件影響下基于CPM的創業企業融資決策實物期權模型
Tavares-G?rtner等(2018)[7]假設創業企業的利潤流服從幾何布朗運動擴散過程,考察了作為創業企業融資決策的一種資本籌集策略CPM.Dixit和Pindyck(1994)[14]指出,帶有離散跳躍的幾何布朗運動模型很適合模擬企業的現金流.例如,一家企業的收益會受到一些不可預測但相當大的變化的影響,這些變化是對好消息或壞消息的反應.因此,不同于文獻[7]的模型,在描述包含突發事件的現實不確定性時,將其設定為帶“跳躍”的幾何布朗運動.本節首先建立刻畫突發事件影響下的企業利潤流的跳躍-擴散模型,然后推導出EN和VC持有的企業成長機會的期權價值,為研究CPM如何影響其結果做好基礎性工作.
2.1 變量描述與模型建立
考慮一家由一個EN擁有的創業企業,通過擴大當前的利潤流(用eEXP>1表示)和給定的資本支出(用k> 0表示),使企業產生正的利潤并保持成長機會.假設EN和創業企業都無法獲得債務融資,這種資本支出應當通過由擁有有限資源的EN和外部融資人支持的一輪股權融資來提供資金,而外部融資人被認為是一個不受資金限制的VC.假設VC可以提供EN所需的部分資金.
使用以下符號表示相關的變量:
ki表示EN提供給創業企業的初始資本,
ka表示EN愿意向創業企業投入的額外資本,
k表示創業企業執行成長戰略所需的資本支出總額,
(k-ka)是VC投入創業企業的資本.
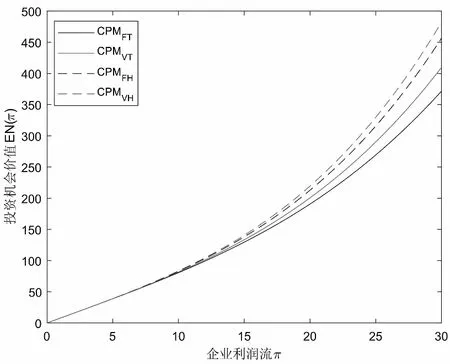
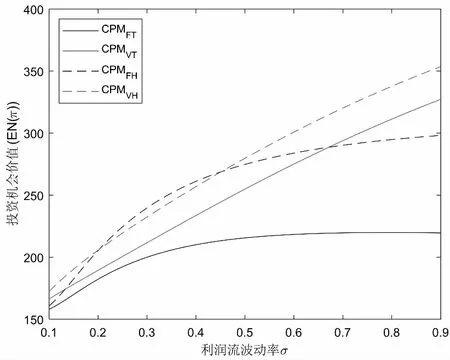
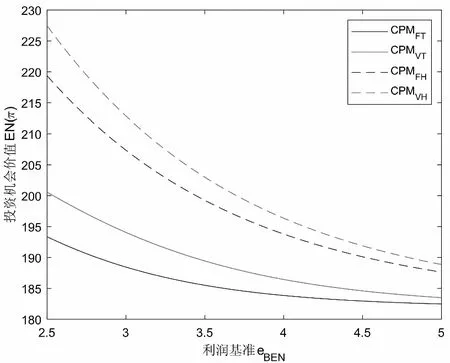
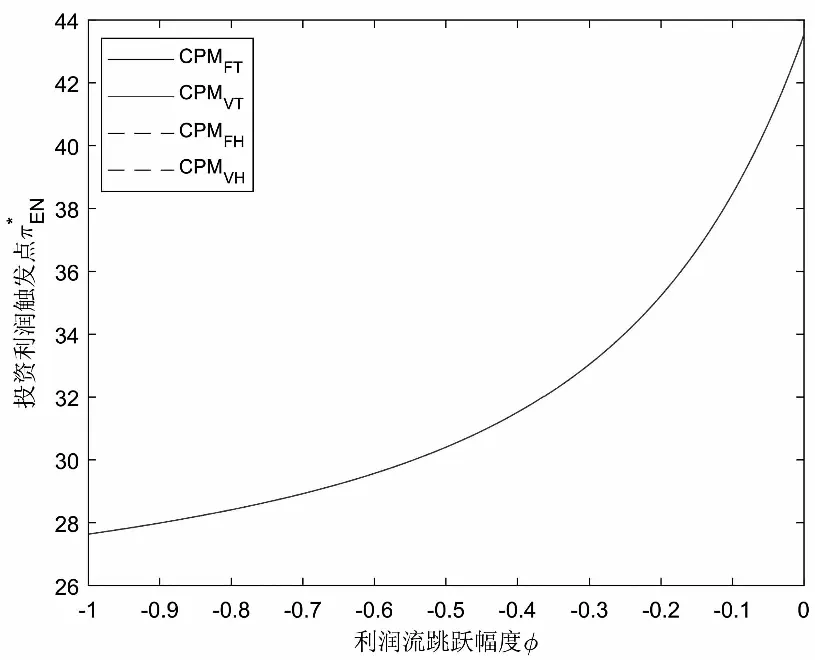
假定雙方在進行某輪股權融資后根據各自對創業企業的出資額來決定其對企業的所有權.經股權融資后EN持有的股權表示為0 創業企業的項目價值(或利潤)受外部市場環境及其經營狀況的影響.假設項目產生連續時間利潤流(t),服從帶Poisson跳躍的混合布朗運動 dπ=απdt+σπdz+φπdq (1) 其中α和σ分別為漂移參數和瞬時波動率參數. 在風險中性條件下,α=r-δ,r>0是無風險利率,δ>0是資產收益率,從而α為風險中性下的漂移,dz是標準維納過程的增量.dq為突發事件變化過程服從平均到達(發生)率為的Poisson過程的增量,并且dz和dq相互獨立,即E(dzdq)=0.因此,dq=0的概率為1-λdt,而dq=1的概率為λdt,換句話說,在充分短的時間區間dt內,項目價值π發生跳躍的概率是λdt.φ 表示跳躍的幅度,滿足-1≤ φ≤0,其中負號表示向下跳躍,模型(1)也稱為跳躍-擴散過程.最后,假定EN和VC認為項目價值(t)服從相同的隨機過程,即EN和VC對項目的價值具有同質信念. 如式(1)所示,在企業利潤流的動態過程中加入的一個跳躍成分,用來描述突發事件對企業利潤流的影響.這種企業盈利的一般設置使得能夠在更符合實際經濟環境的情景下研究創業企業的融資決策,得到比Tavares-G?rtner等(2018)[7]報告的更為穩健的結果. 根據Dixit和Pindyck(1994)[14]的或有權益分析方法,EN持有的投資于創業企業成長機會的期權價值EN()滿足式(2)所示的常微分方程. (2) 上式左邊最后一項為創業企業的當前利潤流,而其余的項表示創業企業持有的增長期權.假設EN(0)=0,則方程(2)的解的一般形式為 (3) 其中A是待定常數,是式(4)所示非線性方程的根. (4) (5) (6) 條件(5)表示EN決定投資成長機會時獲得的收益.條件(6)保證了EN()在>0連續可微. (7) 考慮到VC(0)=0,方程(7)的解的一般形式為 試驗組45(100.00)的滿意度對比對照組滿意程度35(77.78)更高,差異有統計學意義(P<0.05)。 VC(π)=Bπβ, (8) 其中B為待定常數,為非線性方程(4)的正根.相應的邊界條件為 (9) (10) 本節討論求解使得EN和VC愿意共同支持創業企業成長機會的利潤觸發點和最優或有支付.研究發現,EN和VC持有的投資期權的價值和利潤觸發值均與刻畫突發事件的兩個參數和有關. 類似于Tavares-G?rtner等(2018)[7]的方法,將CPM視為二元式看漲期權,而不是股票的普通看漲期權,因為它們的回報實際上是不連續的,即要么是固定金額,要么是線性依賴于標的資產價值的可變金額.因此可以把固定數額的CPM定義為現金或空手看漲二元式期權,如果創業企業達到或超過給定的績效基準,EN應當獲得固定數額的現金. 當CPM是按確定的期限到期時,或有支付可以被建模為傳統的二元式期權[15].對于按期到期的或有支付,假設該期限是由雙方共同決定的,并由t >0給出. 當或有支付是當企業業績達到基準業績時到期,或有支付應當被建模為二元式障礙期權[16]. 根據上述分析,支付日期為確定期限的固定數額或有支付(記為CPMFT)可以被建模為現金或空手看漲期權,其價值如式(11)所示. CPMFT=θFTe-rtN(d2FT), (11) 其中 (12) 其中 (13) 類似地,通過聯立求解方程(9)、(10)和(11)可以推導出在CPMFT下,VC持有的投資于成長機會的期權價值和利潤觸發點為 其中 (14) (15) (16) 不難發現,當λ=0或φ=0,即不考慮突發事件對項目價值的影響時,式(15)與式(16)相同. 這種類型的CPM可以被視為資產或空手看漲期權,如式(17)所示. CPMVT=mVTπ(eEXP-1)e-δtN(d1VT), (17) 其中 通過聯立求解方程(5)、(6)、(17)可以獲得EN投資于成長機會的期權價值,而通過聯立求解方程(9)、(10)、(17)則可以獲得VC投資于成長機會的期權價值,以及雙方各自的最優利潤觸發值,如下式所示. 其中 (18) 并且 其中 (19) (20) 根據Rubinstein和Reiner(1991)[17],假定觸發或有支付的業績基準大于或等于其當前水平,到期日為目標實現時刻且支付固定數額的或有支付(記為CPMFH)可以被看作向上敲入現金或空手看漲二元式障礙期權,其價值如式(21)所示. (21) 其中 (22) (23) (24) 其中 (25) 以及 其中 (26) (27) 對于在達到業績基準時(at hit)到期并支付變動數額的或有支付機制(記為CPMVH),假設業績基準大于或等于其當前水平,可以將這種類型的CPM視為向上敲入資產或空手看漲二元式障礙期權.采用類似于Tavares-Grtner等(2018)[7]的方法,得到其價值如式(28)所示. (28) 其中a,b和z分別由式(22)、式(23)和式(24)定義.進一步,由式(5)、式(6)、式(28)和式(9)、式(10)、式(28)可求得EN和VC投資成長機會的期權價值和他們的最優投資利潤觸發值分別為 其中 (29) 以及 其中 (30) (31) (32) (33) (34) (35) 從中不難發現,對每一種CPM類型,由于EN和VC的最優投資時機具有關于刻畫突發事件的兩個參數和的相同的表達式,因此,在考慮突發事件的影響時,雙方共同投資的最優時機仍與CPM的類型無關. 下面考慮雙方共同投資時或有支付的價值,用CPMF表示固定數額或有支付,通過聯立求解式(3)、式(5)和式(6),可以獲得EN投資于企業成長機會的利潤觸發值為 同樣,通過聯立求解式(8)、式(9)和式(10),得到VC投資企業成長機會的利潤觸發值為 (36) (37) 總的來說,或有支付對于EN表示其持有的關于投資成長機會的期權的資產,對于VC則表示其持有的關于投資成長機會的期權的同等負債,當控制影響可變或有支付的隨機參數時,最優投資時機不受或有支付機制設計的影響.但是,在考慮突發事件的情況下,不同類型的最優或有支付均受Poisson跳躍過程的參數的影響. 接下來,將通過數值分析來說明本節獲得的解析結果背后的經濟意義,并討論突發事件的兩個參數對最優投資時機的影響. 本節通過一個數值例子來說明突發事件影響下基于或有支付的融資決策的相關結論.利用MATLAB軟件進行數值模擬,給出最優或有支付和最優投資時機.分別研究當前利潤流、利潤流波動率、業績基準對投資機會價值的影響,以及突發事件的跳躍幅度(或影響規模)和平均發生率對最優投資時機的影響. 借鑒相關文獻設定影響創業企業投資期權價值及其標的利潤觸發點的參數[7,9,14],相關參數的具體取值見表1.根據式(4)可求得的數值解,同時,經計算可得QEN=65.4%以及QVC=34.6%. 表1 參數設置 表2給出了在考慮突發事件的影響下,當創業企業的利潤流服從式(1)的跳躍-擴散過程時,根據第3節中的理論結果計算得到的相應最優固定數額或有支付*、最優可變數額或有支付m*以及最優利潤觸發點π*. 表2 最優CPM 表2的數值結果顯示,當企業利潤流服從跳躍-擴散過程,且雙方同意業績基準在短期內可達到時,確定期限支付的CPM比業績基準實現時刻支付的CPM產生更高的支付數額或支付倍數.最后一列數據顯示,最優決策時投資時機與或有支付機制的類型無關,這驗證了3.5節的結論. 不同的或有支付機制價值不同,其潛在的投資機會價值也不同,表2的結果也驗證了這一點.對于固定數額CPM,支付日期分別為固定期限和業績目標實現時刻,會支付不同的數額.對于可變數額CPM,在確定期限和業績目標實現時刻支付的CPM,其支付倍數也是不同的.下面從EN的角度分析主要參數對投資機會價值和最優投資時機的影響. 4.2.1 當前利潤流和投資機會價值 假設m=4.0,=150,圖1說明了EN在π<π*范圍內所擁有的投資機會的價值的直觀含義.其中,虛線表示在固定期限支付的或有支付機制,而實線則表示在目標實現時刻支付的或有支付機制. 圖1 企業利潤流與EN持有的投資機會的價值 可變金額CPM比固定金額CPM更有價值,因為可變數額CPM可能產生正的支付或更低的盈利水平,并且當盈利能力超過其基本閾值時,可能產生比固定金額CPM更高的收益. 4.2.2 利潤流波動率和投資機會價值 本節討論利潤流波動率如何影響每一種或有支付機制下投資成長機會的期權的價值.假設m=4.0,=150,0=20. 圖2表明,利潤流的變化遵循跳躍擴散模型的情況下,波動性增加會給投資機會帶來額外的價值,并且可變或有支付對利潤流波動率的變化更敏感.對于可變數額或有支付,波動率越高投資機會價值越大,表明波動率較高的企業更應該選擇可變或有支付,而對于固定數額或有支付,較高水平的波動性下的投資機會價值趨于穩定. 圖2 利潤流波動率與EN持有的投資機會的價值 4.2.3 業績基準和投資機會價值 由于業績基準影響獲得或有支付的可能性,因此預期二者之間會出現負相關關系.假設m=4.0,=150,0=20.對一系列高于預期利潤增長的業績基準(即eBEN>eEXP),圖3顯示了EN持有的投資于成長機會的期權價值之間的關系. 圖3 業績基準與EN持有的投資機會的價值 雙方約定的基準越高,EN實際獲得或有支付的可能性就越低,亦即其投資機會的價值越低. 4.2.4 利潤流跳躍幅度和最優投資時機 針對四種類型的CPM,考察Poisson跳躍過程的跳躍幅度參數對 EN投資的最優利潤觸發點(最優投資時機)的影響.假設m=4.0,=150,0=20.圖4顯示了EN投資的利潤觸發點與跳躍幅度的關系.跳躍幅度越大,利潤觸發點越小(負號表示利潤流跳躍方向,即向下).較大意味著投資機會的價值較小(利潤流將會下降較大的比例),立即投資的機會成本較小,因此,跳躍幅度越大,EN更傾向立即投資而不是等待. 圖4 跳躍幅度與投資時機 4.2.5 事件平均發生率和最優投資時機 圖5 事件發生率與投資時機 引入Poisson跳躍過程描述突發事件的發生導致企業的利潤流出現的離散跳躍,應用實物期權方法通過數理推導給出了四種不同類型或有支付下的最優或有支付數額表達式與最優投資時機. 研究發現,考慮突發事件的影響時,雙方同時投資的最優時機與或有支付機制的類型選擇無關.數值分析結果表明,在業績基準實現時刻支付的或有支付比在確定期限支付的或有支付具有更高的價值,可變數額或有支付比固定數額或有支付具有更高的投資機會價值.波動率越高投資機會價值越大,對于固定數額或有支付,較高水平的波動性下投資機會價值趨于穩定.突發事件的平均發生率越大,雙方共同投資的時機越早.利潤流跳躍幅度越大,共同投資的時機也越早. 研究結果可以幫助提高創業企業家和風險投資家之間達成協議的可能性,促進創業企業順利融資.但是對現實情況的考慮還可以更加深入一些.創業企業家和風險投資家對創業企業的利潤增長有不同預期,突發事件對利潤流的影響為隨機影響等,可以進一步展開系統深入的研究.2.2 企業家持有CPM的期權價值
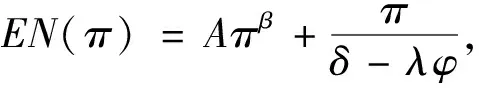

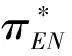
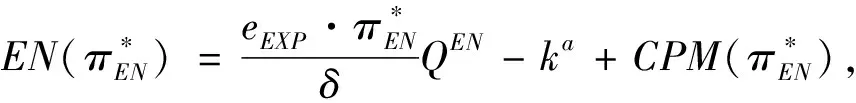
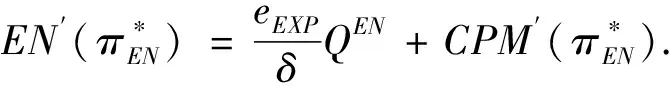
2.3 風險投資家持有CPM的期權價值
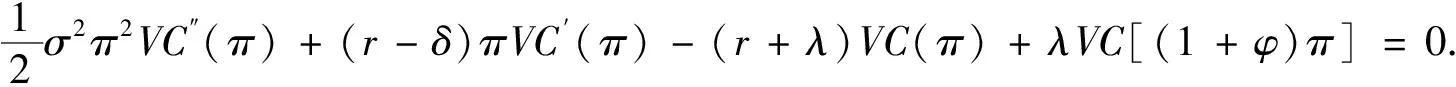
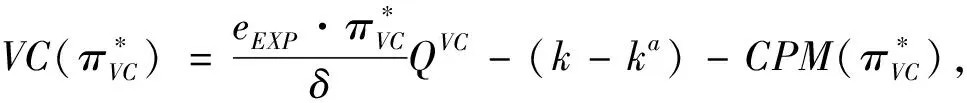


3 突發事件影響下四種CPM類型的創業企業最優融資策略
3.1 基于確定期限支付固定數額CPM的融資策略

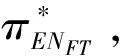
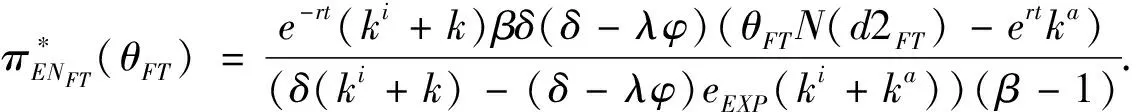



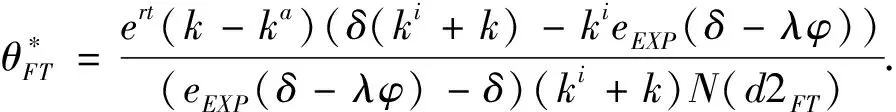

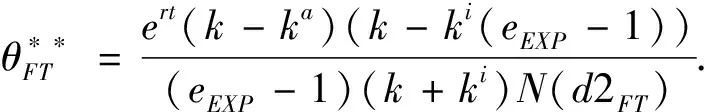
3.2 基于確定期限支付可變數額CPM的融資策略

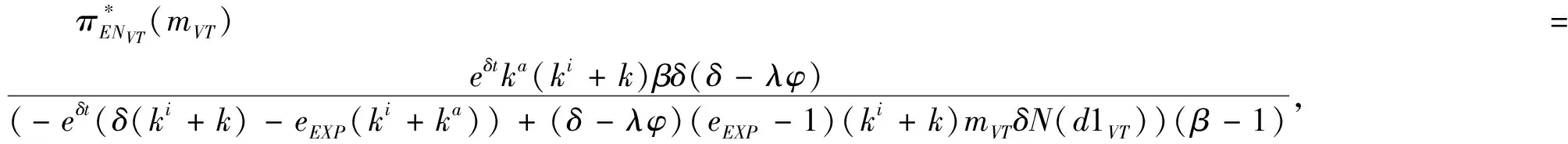
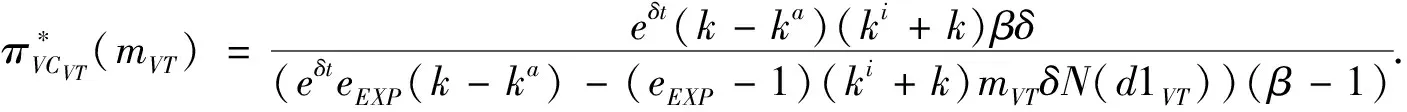

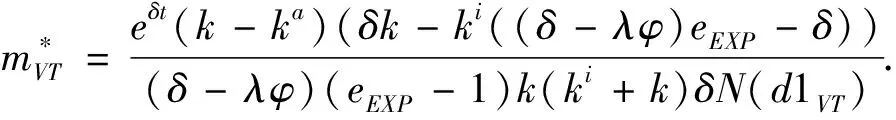
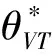
3.3 基于目標實現時刻支付固定數額CPM的融資策略
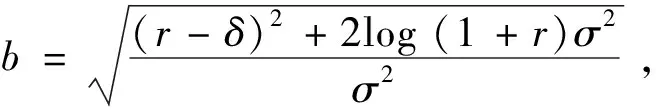
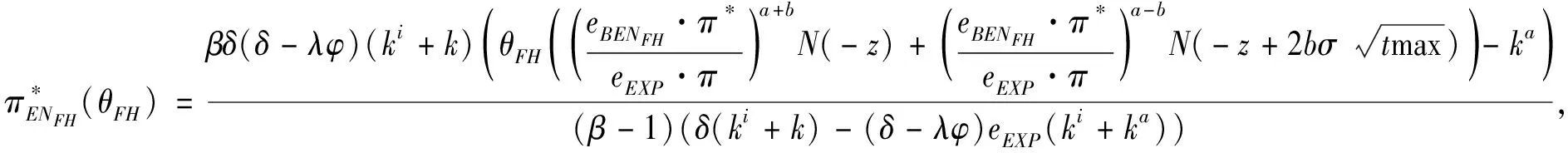
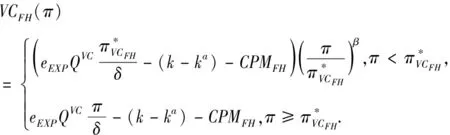

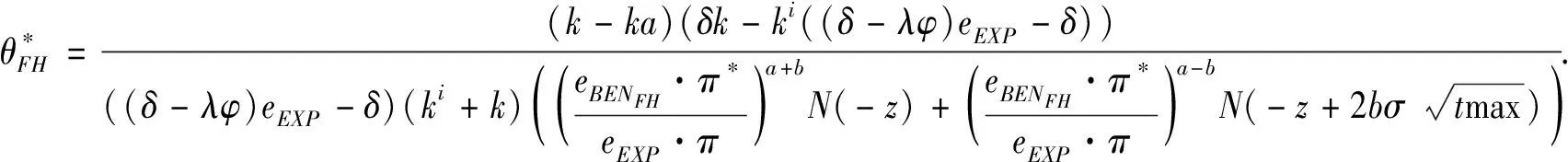
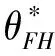
3.4 基于目標實現時刻支付可變數額CPM的融資策略

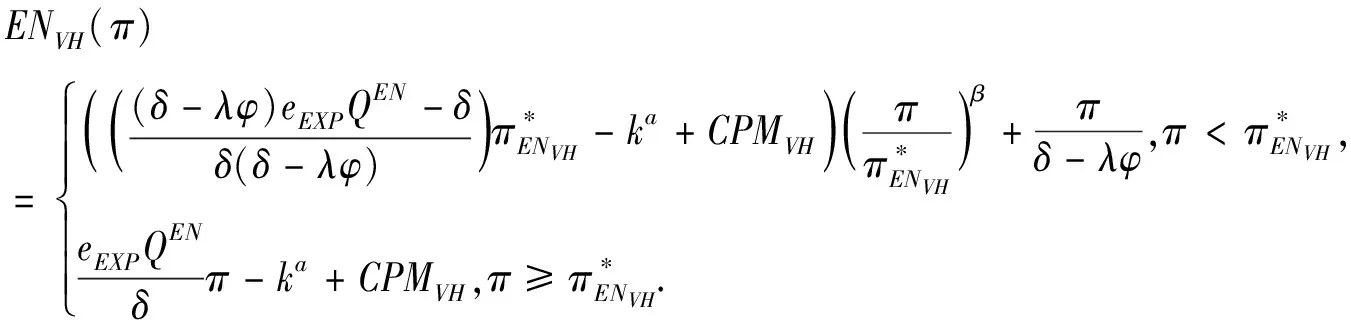
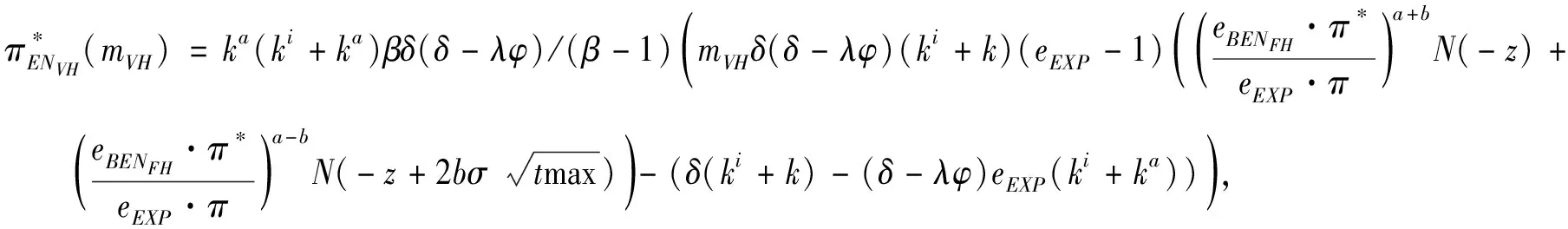

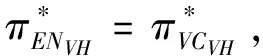
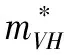
3.5 CPM與最優投資時機


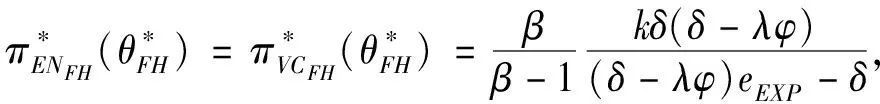

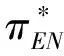
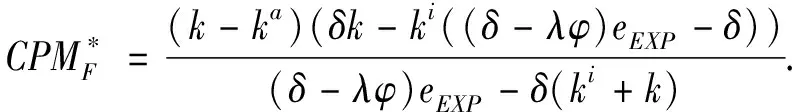
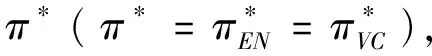

4 數值模擬及敏感性分析
4.1 參數設置
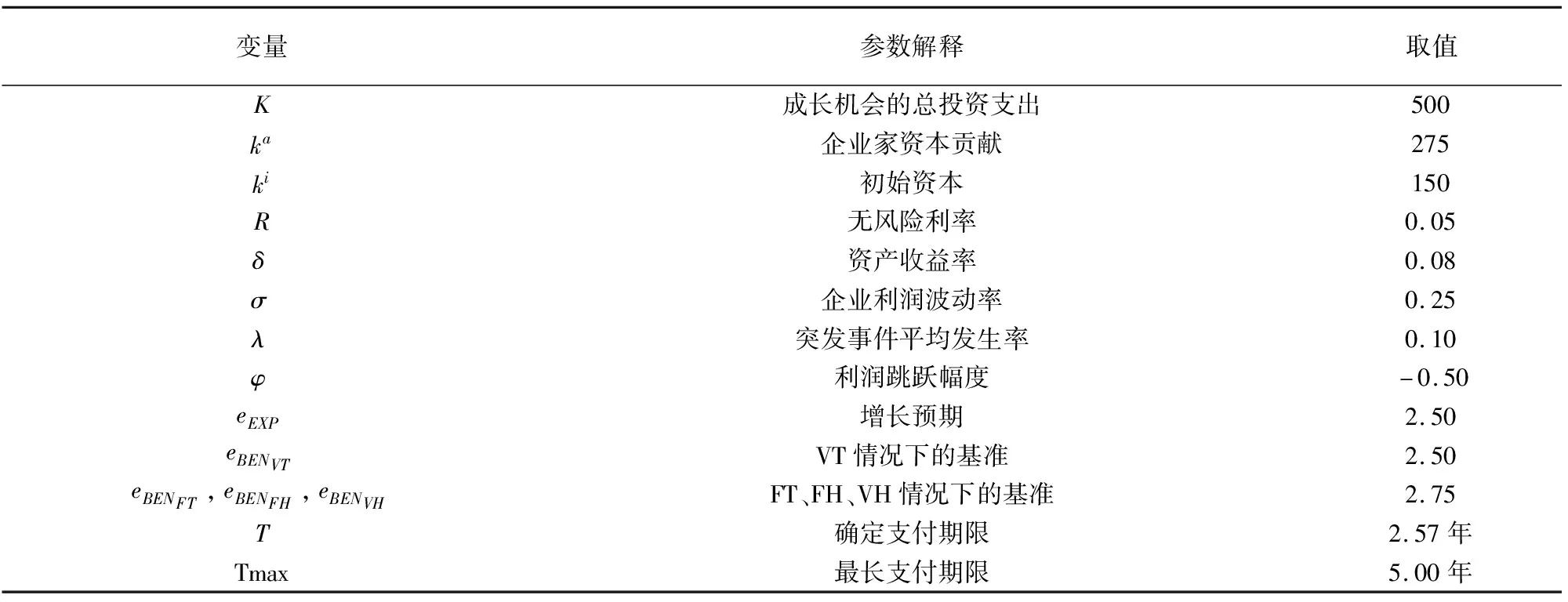
4.2 結果分析


5 結 論

