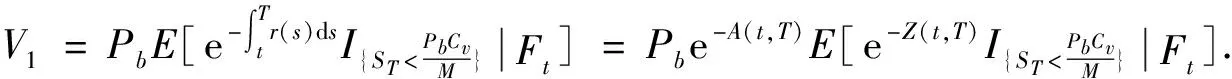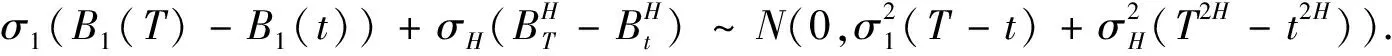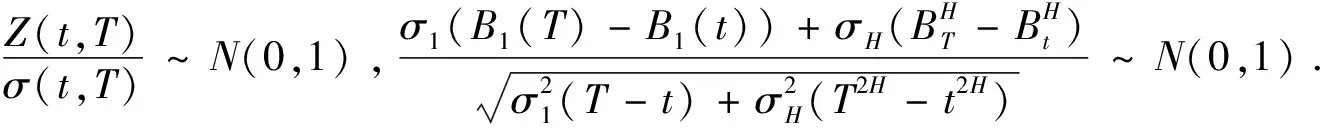混合分數布朗運動下分離交易可轉債的定價*
陳飛躍,陳 煜,楊 蓉,龔海文
(1.保險職業學院 金融系,湖南 長沙 410114;2.長沙理工大學 數學與計算科學學院,湖南 長沙 410114)
1 引 言
分離交易可轉債(Separable and Convertible Bonds)是上市公司公開發行的 “認股權”和“債券”分離交易的可轉換公司債券[1].分離交易可轉債賦予持有人在債券到期前規定的時間內按照約定的執行價格和行權比例購買上市公司股票的權利.當然,到期前若股票市價低于行權價格,則投資者將放棄認股權.當分離交易可轉債的持有人行使了期權后,依舊持有債券,仍可定期獲取利息,到期收回本金,故分離交易可轉債具有一次發行兩次融資的優點.投資者最初購買分離交易可轉債,對發行人來說屬于“債權融資”,若投資者后來行使了期權,繳納認股款則屬于“股權融資”.而普通可轉債的持有人在債券到期前一旦執行轉換,則其債權就不復存在了.因此,人們通常認為分離交易可轉債是一種“買債券送權證”的新型衍生金融工具.
20世紀70年代美國證券市場通過金融創新,率先提出了分離交易可轉債概念,經過40多年的發展,目前分離交易可轉債已成為美國證券市場比較成熟的一種新型衍生證券.Ingersoll[2,3]最早將Black-Sholes 期權定價公式用于可轉債定價,通過分析投資者的最優轉換策略以及發行人的最優贖回策略,得到了可轉債定價的顯示表達式.Finnerty[4]通過對機構投資者進行調查發現,分離交易可轉附帶權證帶來的折價發行會增加投資者的稅收負擔,從而會使投資者望而卻步.近年來,國內一些學者也積極探討了可轉債的定價問題.李爭華[5]以寶鋼分離交易可轉債為例,利用稀釋效應的期權定價模型詳細研究了其定價問題,得出結論:寶鋼分離交易可轉債的“債券”定價比較合理,但“權證”定價稍許偏高于其實際價格.駱樺、沈紅梅[6]基于國內可轉債市場的實際情況,應用Black-Shocles模型推導出分離交易可轉債定價的表達式,并分析了分離交易可轉債帶來的股權稀釋效應.我國學者江良、林鴻熙等[7]探討了基于隨機利率模型下可轉換債券的定價問題,研究表明:常數利率和隨機利率對可轉換債券價格的影響不存在顯著的差異.
以上可轉債定價問題研究均以股票市價服從標準布朗運動為假設前提.Peter[8]首先提出分形市場假說,通過分析股票價格和外匯匯率等金融資產的波動,發現金融市場存在分形結構和非周期循環的特點.同時,行為金融學的大量實證研究也表明:股票、外匯、基金等金融資產的價格過程具有自相似性、長期依賴性、長記憶性等特征,并不是隨機波動的,金融資產的對數收益率并不服從正態分布,而是呈現出“尖峰厚尾”的特點.由于分數布朗運動是一種高斯過程,具有自相似性、厚尾性、長期相關性以及加法不變性等性質,這些性質使得分數布朗運動能較好地擬合股票、外匯、基金等金融資產的變化過程.Duncan等[9]、Hu和?ksendal[10]、Elliott和Van等[11]在這方面做了一些開創性貢獻,他們利用Malliavin隨機分析理論和Wick積的概念,把分數布朗運動的積分定義為FWIS隨機積分(Fractional Wick ItSkorohold integral,FWIS integral),并證明了基于FWIS積分框架和Wick自融資策略的分數B-S金融市場模型中無強套利機會,并且金融市場是完備的,隨后,Necula[12]在FWIS積分框架下,分別利用擬條件期望和delta對沖法推導出分數B-S公式.陳飛躍[1]構建了股票價格遵循分數布朗運動下分離交易可轉債的定價模型,并推導出了其風險中性定價公式.
然而,Hurst參數H>1/2的分數布朗運動既不是馬爾科夫過程,也不是半鞅,不能用通常定義的隨機積分進行分析,從而分數布朗運動在金融上的應用并非易事.Bj?rk和Hurt[13]的研究表明Wick資產組合導致無套利,但定義自融資交易策略受到嚴格的限制.因此,盡管基于Wick積分的分形市場被認為一個完美的數學結構,但其在金融中的適用性受到限制.當Hurst參數H>1/2時,混合分數布朗運動是一個特殊的長記憶過程.為了克服用分數布朗運動描述金融資產價格變化時存在的缺陷,同時考慮金融資產價格過程所具有的長記憶性特征,使用混合分數布朗運動能更好地來刻畫金融資產的價格變化過程.Sun[14]關于混合分數布朗運動下的歐式匯率期權定價研究結果支持了以上結論.
目前,國內外還很少有文獻研究混合分數布朗運動下分離交易可轉債的定價問題.本文假定股票價格變動由混合分數布朗運動驅動和市場利率服從Vasicek過程的條件下,建立了分離交易可轉債定價的金融市場偏微分方程.通過求解偏微分方程、并利用無套利定價原理得到了分離交易可轉債定價的顯示解,從而為研究分形市場中金融衍生品估值方法提供參考.用混合分數布朗運動驅動的隨機偏微分方程刻畫股價變化,其中表征收益率長程自相關性的Hurst參數H滿足1/2 分離交易可轉債通常包括:標的股票、票面利率、行權價格、附權證比例、行權比例、行權期限等要素. 1)標的股票:即分離交易可轉債發行公司發行的股票,如“江西銅業可轉債”的標的股票就是江西銅業股票. 2)票面利率:就是分離交易可轉債發行時規定的債券部分的利率,由于分離交易可轉債包含了認股權證,故其票面利率通常低于普通債券利率和銀行利率. 3)執行價格:即行權價格,是投資者在行使認購權時購買標的股票的協議價格. 4)附權證比例:是指發行人給投資者購買的每份分離交易可轉債免費派送的股票權證的數量. 5)行權比例:是指每份股票權證可以認購發行公司股票的數量. 6)行權期限:通常是指分離交易可轉債發行之后,發行人規定的從某時點開始至債券到期日之間持有人可以行使認股權的這段時間. 分離交易可轉債的價值等于“債券”價值與“股票看漲期權”價值之和,其到期時的價值為 其中,M表示分離交易可轉債的票面價值,Pb=MeiT表示按票面利率i連續復利計息得到的債券到期時的價值,Cv表示執行價格,T表示到期時間,ST表示T時刻的標的股票的價格,α表示附權證比例,β表示行權比例. 1)定義 設(Ω,F,P)是一完備概率空間,混合分數布朗運動是由相互獨立的標準布朗運動和分數布朗運動組成的一個線性組合,由下式給出(t∈R+): 證明見參考文獻[15]. 1)金融市場無摩擦,即稅收和交易費可以忽略不計; 2)所有證券可以無限制的細分,證券交易是連續進行的,且交易頭寸和交易方向都不受限制,無最大持有定額限制; 3)所有投資者可以及時免費獲得充分的市場信息,市場不存在無風險套利機會; 4)暫不考慮分離交易可轉債的違約風險. 1)由于可轉債不是短期衍生證券,從而不將市場利率設為常數,假定市場利率服從Vasicek過程,即 dr(t)=k(θ-r(t))dt+δdB2(t). (1) 其中k為均值回復率,θ為利率均值,k,θ,δ均為正常數,B2(t)是一標準布朗運動; 2)假定標的股票的價格{S(t)或St,t≥0}滿足如下隨機微分方程(SDE): (2) (3) 根據Nualart和Taqqu[16]中的Wick It公式: 從而對?T>t>0,有 (4) 證明由方程(1)可得:dr(t)+k·r(t)dt=kθdt+δ·dB2(t),等式兩邊同時乘以ek·t,則有 ek·tdr(t)+k·r(t)·ek·tdt=ek·tkθdt+ek·tδ·dB2(t). 對t≤u≤T,上述等式兩邊在[t,u]積分,得到 將上式右邊最后一個二重積分交換積分次序可得 (5) 由文獻[17]可知 即,Z(t,T)~N(0,σ2(t,T)). 4.1 引理2設Z1~N(0,1),Z2~N(0,1),Cov(Z1,Z2)=ρ,則對任意實數a,b,c,d,s,有下式成立: 4.2 定理假定股票價格變動由混合分數布朗運動驅動,且市場利率遵循Vasicek過程,則分離交易可轉債在到期前任意時刻t的理論價值為 (6) 證明由無套利定價原理(風險中性定價原理)可知, 記上式中的第一項為V1,第二項為V2,先計算第一項V1, 注意到:Z(t,T)~N(0,σ2(t,T)),B1(T)-B1(t)~N(0,T-t), 于是,由引理1得 (7) 再計算V2, (8) 將式(8)中的兩項分別記為V21,V22,則V21與V1的計算方法相同,可得: (9) 由式(5)可得 (10) 將V1,V21,V22分別代入V(t,T,r(t),St)中,得 V(t,T,r(t),St)=2 預備知識
2.1 分離交易可轉債的構成要素
2.2 分離交易可轉債的價值
2.3 混合分數布朗運動的定義


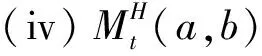


3 混合分數布朗運動下分離交易可轉債定價的金融市場模型
3.1 模型假設
3.2 金融市場模型
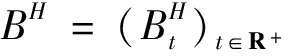
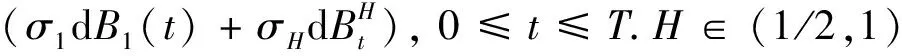
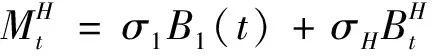

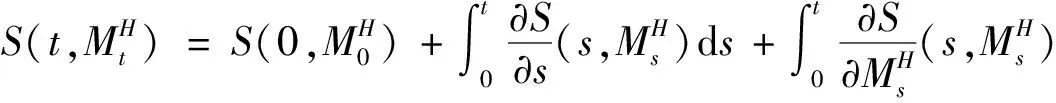
3.3 引理1 隨機微分方程(1)的解為:對t≤u≤T,有
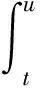
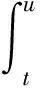
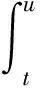
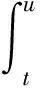
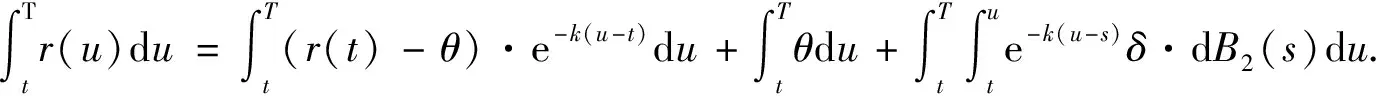
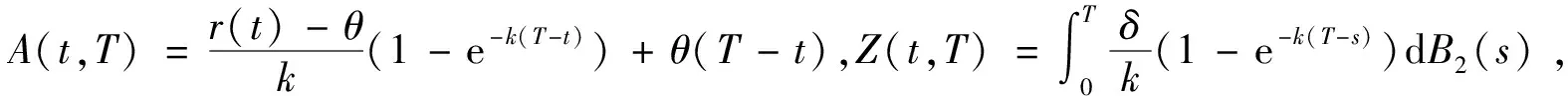
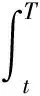
4 分離交易可轉債價值的主要結論