基于ARMA模型的共享單車的投放預(yù)測(cè)與管理*
何郁波,曾 楨,蘭燕鴻,黃遵杰
(懷化學(xué)院 數(shù)學(xué)與計(jì)算科學(xué)學(xué)院,湖南 懷化 418008)
1 引 言
在移動(dòng)互聯(lián)網(wǎng)和智能手機(jī)APP等創(chuàng)新技術(shù)的驅(qū)動(dòng)下,城市慢行交通領(lǐng)域作為一種新型事物逐漸出現(xiàn).在城市居民的出行領(lǐng)域,打車類應(yīng)用軟件的發(fā)展逐漸趨于穩(wěn)定,但民眾在短途的出行中“最后一公里”出行的問題始終沒有得到解決.近年來,共享單車的出現(xiàn),讓民眾多了一種綠色的出行方式可以選擇[1].共享單車的最大價(jià)值在于民眾出行的“最后3公里”,其無樁借還的模式相比于政府公共租賃自行車,使民眾借還單車更加快速和便捷.同時(shí),共享單車引導(dǎo)政府部門重視慢行交通系統(tǒng)的建設(shè),倡導(dǎo)民眾更多選擇綠色出行的方式,這些方面能在一定程度上緩解城市交通擁堵、改善城市環(huán)境.然而,共享單車作為新興事物,隨著共享單車平臺(tái)企業(yè)在各大城市開始大量投放單車,共享單車的停放、安全出行等問題引起了社會(huì)的關(guān)注[1].
2 模型的基本知識(shí)
基于時(shí)間序列分析的方法,本文將對(duì)某一個(gè)定點(diǎn)對(duì)于共享交通工具的使用情況進(jìn)行分析預(yù)測(cè),從而為相關(guān)部門提供共享交通工具的投放與管理提供依據(jù).所謂時(shí)間序列,就是按照時(shí)間的順序?qū)⒛撤N現(xiàn)象的某一個(gè)統(tǒng)計(jì)指標(biāo)的數(shù)值排列而形成的序列.對(duì)時(shí)間序列進(jìn)行觀察、研究,尋找它變化發(fā)展的規(guī)律,預(yù)測(cè)它將來的走勢(shì).常見的預(yù)測(cè)方法有利用回歸的方式建立相應(yīng)的模型預(yù)測(cè),如利用支持向量機(jī)回歸、線性回歸等預(yù)測(cè)方法[2];有采用徑向基函數(shù)(RBF)神經(jīng)網(wǎng)絡(luò)模型對(duì)時(shí)間序列進(jìn)行擬合及預(yù)測(cè)[3].
在時(shí)序分析中,求和自回歸移動(dòng)平均(autoregressive integrated moving average, ARIMA)模型是時(shí)間序列預(yù)測(cè)方法最為經(jīng)典的模型.將具有如下結(jié)構(gòu)的模型稱為ARIMA(p,d,q)模型:
(1)
利用ARIMA模型對(duì)一些重要時(shí)序進(jìn)行預(yù)測(cè)和應(yīng)用目前已取得了大量非常重要的結(jié)果.文[4]針對(duì)工控系統(tǒng)現(xiàn)場控制層數(shù)據(jù)進(jìn)行分析,利用數(shù)據(jù)的時(shí)序性,通過ARIMA模型預(yù)測(cè)出后續(xù)時(shí)刻系統(tǒng)數(shù)據(jù)的信息.李勃旭等運(yùn)用研發(fā)的數(shù)據(jù)采集系統(tǒng)對(duì)新上線地鐵門的夾緊力進(jìn)行實(shí)時(shí)采集,對(duì)于采集后的時(shí)序數(shù)據(jù)利用ARIMA模型與EMD-ARIMA模型對(duì)夾緊力峰值的均值和標(biāo)準(zhǔn)差隨累計(jì)運(yùn)行時(shí)間的變化趨勢(shì)進(jìn)行預(yù)測(cè),獲得了非常有用的結(jié)論[5].針對(duì)煙草行業(yè)的供給,文[6]利用ARMA模型對(duì)煙草的供給和配送進(jìn)行了預(yù)測(cè).關(guān)于ARIMA模型與其他模型相結(jié)合的方法,也有諸多的文獻(xiàn)進(jìn)行了研究.王濤采用ARIMA模型、BP神經(jīng)網(wǎng)絡(luò)模型和Holt指數(shù)平滑模型對(duì)1995-2017年上海電力需求數(shù)據(jù)進(jìn)行建模分析,構(gòu)建了組合模型,并依據(jù)組合模型預(yù)測(cè)了未來五年的上海市電力需求量趨勢(shì)[7],擬合的效果較好,有利于電力供應(yīng)單位穩(wěn)定電力供應(yīng),促進(jìn)經(jīng)濟(jì)社會(huì)發(fā)展.同時(shí),結(jié)合ARMA和GARCH建立預(yù)測(cè)模型的成果表明:在擬合效果上,ARMA-GARCH模型較優(yōu);在預(yù)測(cè)效果方面,ARMA模型最優(yōu)[8].其他一些相關(guān)的成果可參閱以上所列的文獻(xiàn)及其中所介紹的相關(guān)參考文獻(xiàn).
3 數(shù)據(jù)預(yù)處理
數(shù)據(jù)預(yù)處理及相應(yīng)分析的流程圖如圖1所示.以湖南省懷化市第一人民醫(yī)院為觀測(cè)點(diǎn),對(duì)2018年6月27日—2018年9月15日的觀測(cè)統(tǒng)計(jì),以7:30—18:30為觀測(cè)時(shí)間段,共獲得81天的共享單車日使用臺(tái)·次,結(jié)果見表1.

圖1 確定時(shí)間序列模型流程圖
將原始序列記為X-user,對(duì)序列X-user進(jìn)行純隨機(jī)性檢驗(yàn),即白噪聲檢驗(yàn).利用SAS軟件對(duì)序列X-User進(jìn)行白噪聲檢驗(yàn)結(jié)果如表2所示.表2的白噪聲檢驗(yàn)結(jié)果表明,延遲6,12和18期的χ2統(tǒng)計(jì)量的相伴概率都小于顯著性水平5%,因此原序列X-user屬于非白噪聲序列,具有相關(guān)性.

表2 白噪聲檢驗(yàn)結(jié)果
序列X-user的時(shí)序圖見圖2,由時(shí)序圖可知該序列是平穩(wěn)序列,均值為52.6667,標(biāo)準(zhǔn)差18.3397.
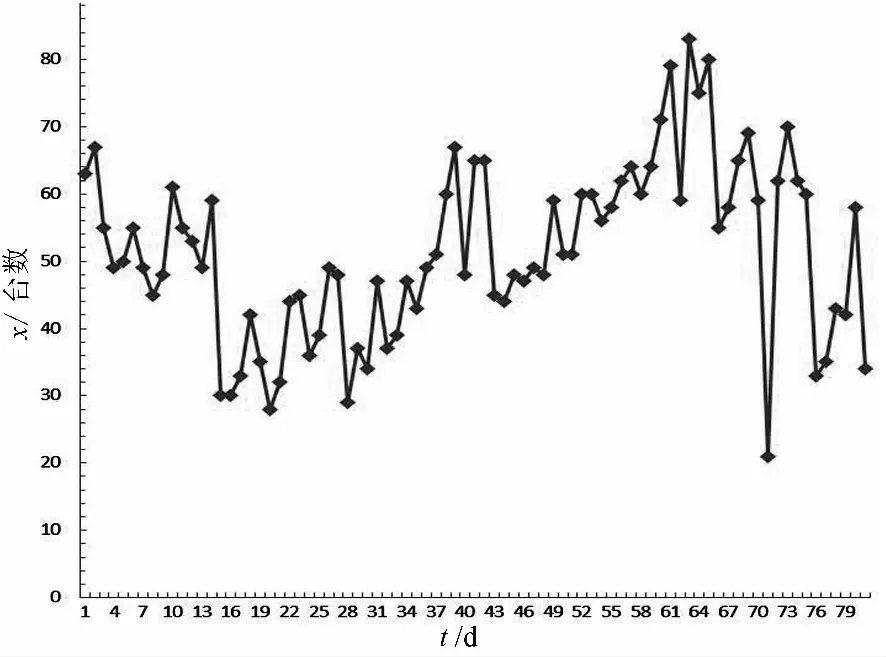
圖2 原始序列的時(shí)序圖
4 模型的建立與預(yù)測(cè)
為了對(duì)模型進(jìn)行識(shí)別并定階,采取對(duì)序列的自相關(guān)以及偏自相關(guān)的拖尾或截尾的性質(zhì)來進(jìn)行判別.利用SAS對(duì)X-user序列進(jìn)行分析,自相關(guān)和偏自相關(guān)系數(shù)圖3.

圖3 序列X-user的自相關(guān)圖
由自相關(guān)圖可知序列X-user的自相關(guān)圖延遲1期以后雖然在2倍標(biāo)準(zhǔn)差的范圍之內(nèi),但是一直到延遲12期自相關(guān)系數(shù)保持一定的拖尾性.圖4序列X-user的偏自相關(guān)系數(shù)在延遲1期以后出現(xiàn)截尾性,因此嘗試擬合AR(1)模型.

圖4 序列X-user的偏自相關(guān)圖
使用條件最小二乘估計(jì)方法,確定AR(1)模型的口徑為
(2)
且Var(εt)=299.6057.
殘差的白噪聲檢驗(yàn)顯示延遲6階、12階、18階、24階所對(duì)應(yīng)的LB檢驗(yàn)統(tǒng)計(jì)量的P值均顯著大于0.05,所以該AR(1)模型是顯著有效的.

表3 殘差的白噪聲檢驗(yàn)結(jié)果
對(duì)參數(shù)的顯著性進(jìn)行檢驗(yàn),結(jié)果顯示兩參數(shù)t統(tǒng)計(jì)量的P值都小于0.05,因此兩個(gè)參數(shù)都顯著.因此AR(1)模型是序列的有效擬合模型.

表4 條件最小二乘估計(jì)結(jié)果
為了更好地?cái)M合原始序列,搜索最優(yōu)的模型.通過序列自相關(guān)圖2顯示,該序列自相關(guān)系在5階以后表現(xiàn)一定的截尾性,另外偏自相關(guān)系數(shù)帶一定的拖尾性,因此考慮用MA(5)模型進(jìn)行擬合.同樣采用條件最小二乘法對(duì)相關(guān)參數(shù)進(jìn)行估計(jì),得到MA(5)模型口徑為
X-usert=52.71613+(1+0.35179B+0.07076B2+0.06588B3+0.16252B4+0.18323B5)εt且Var(εt)=300.9124.
殘差的白噪聲檢驗(yàn)結(jié)果顯示擬合的模型顯著有效,另外對(duì)于參數(shù)進(jìn)行顯著性檢驗(yàn)結(jié)果為所有待估的參數(shù)均顯著.
為了比較兩個(gè)模型的優(yōu)劣性,引入AIC和SBC信息準(zhǔn)則.檢驗(yàn)結(jié)果如表5.

表5 擬合模型的AIC和SBC信息準(zhǔn)則結(jié)果
最小信息量的檢驗(yàn)顯示,AR(1)模型無論使用AIC準(zhǔn)則還是SBC準(zhǔn)則均優(yōu)于MA(5)模型.為了避免漏掉最優(yōu)的模型,我們采用在IDENTIFY命令中增加一個(gè)可選命令MINICp=(0:5),q=(0:5),獲得原始序列中所有自相關(guān)延遲階數(shù)小于等于5,移動(dòng)平均延遲階數(shù)也小于等于5的ARMA(p,q)模型.
由表6的最小信息準(zhǔn)則結(jié)果可知,在自相關(guān)延遲階數(shù)和移動(dòng)平均延遲階數(shù)小于等于5的所有ARMA(p,q)模型中,BIC信息量相對(duì)最小的是BIC(1,3)=5.720673,即ARMA(1,3)模型.采用條件最小二乘估計(jì),各參數(shù)的估計(jì)值結(jié)果見表7.估計(jì)結(jié)果顯示,所有的參數(shù)均顯著(t檢驗(yàn)統(tǒng)計(jì)量的P值均小于0.05).
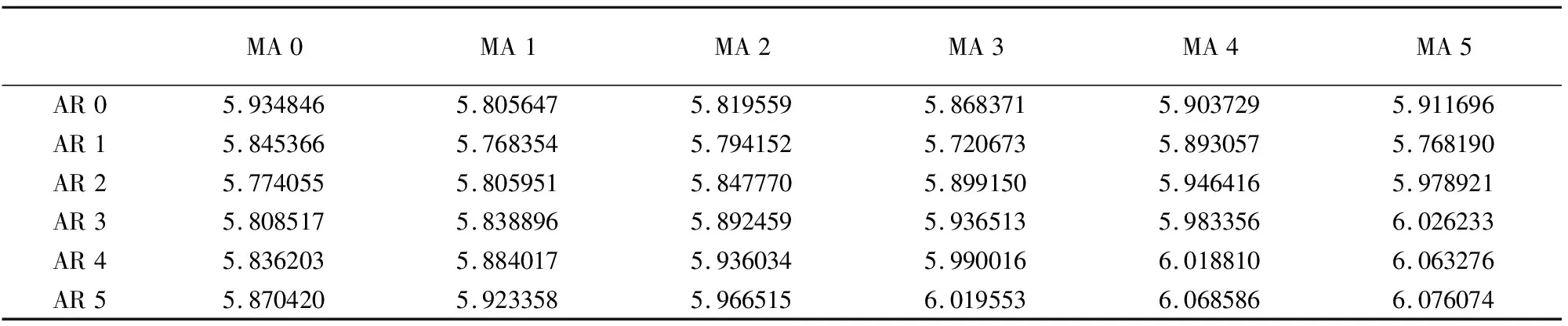
表6 最小信息準(zhǔn)則結(jié)果

表7 ARMA(1,3)模型參數(shù)的條件最小二乘估計(jì)結(jié)果
新模型ARMA(1,3)的殘差自相關(guān)檢驗(yàn)結(jié)果表8顯示,由于延遲各階的LB統(tǒng)計(jì)量的P值均顯著大于α(α=0.05),所以該擬合模型顯著有效.

表8 ARMA(1,3)模型的殘差自相關(guān)檢驗(yàn)結(jié)果
擬合模型為
(3)
根據(jù)上述所得模型,利用SAS軟件對(duì)第82,83,84,85,86期共5期懷化市第一人民醫(yī)院共享單車的使用進(jìn)行預(yù)測(cè),預(yù)測(cè)結(jié)果和實(shí)際的觀察結(jié)果如表9所示.

表9 共享單車的短期預(yù)測(cè)結(jié)果
從表9的預(yù)測(cè)結(jié)果與實(shí)際值的比較可知,模型對(duì)于短期的預(yù)測(cè)具有較高的吻合度,共享單車日使用臺(tái)數(shù)預(yù)測(cè)95%的置信區(qū)間很好的包含了實(shí)際值.具體的預(yù)測(cè)結(jié)果見圖5.圖中實(shí)線所顯示的為預(yù)測(cè)值,虛線所夾部分為置信水平為95%的置信區(qū)間.

圖5 共享單車日使用臺(tái)數(shù)預(yù)測(cè)的95%置信區(qū)間結(jié)果
4 結(jié) 論
采用ARMA模型對(duì)2018年6月27日—2018年9月15日期間某一固定地點(diǎn)共享單車的使用數(shù)據(jù)進(jìn)行建模分析,利用SAS軟件對(duì)所建立模型的有效性、參數(shù)的顯著性進(jìn)行了檢驗(yàn),從而獲得了共享單車使用所滿足的模型口徑.利用訓(xùn)練樣本和檢驗(yàn)樣本對(duì)所建立的模型進(jìn)行了檢驗(yàn),結(jié)果表明所建立的模型擬合效果較好,短期預(yù)測(cè)精度較高,從而對(duì)管理部門的投放和管理工作提供了可靠的依據(jù).

