基于符號的關節臂矩陣運算實現

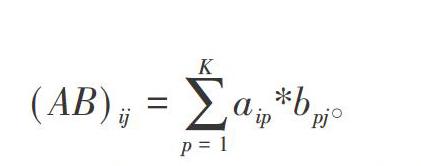

摘要:針對D-H建模[1]的機械臂齊次變換矩陣的旋轉平移運算參數多且運算過程煩瑣問題,本文探討了正、逆運動學中基于字符多項式矩陣運算的化簡和應用,解決了推導繁復的問題,結果可讀性強,可大幅度減少建模設計周期。
關鍵詞:機械臂;字符多項式;矩陣乘法;逆矩陣
中圖分類號:TP393 文獻標識碼:A
文章編號:1009-3044(2020)27-0211-02
開放科學(資源服務)標識碼(OSID):
多關節機械臂在制造、醫療等眾多領域因其具有精準、高效等特點應用日益廣泛嘲。要解決機械臂能耗低,速度快,壽命長問題,合理建模是一個關鍵環節。而采用DH表示法建模是當下行之有效的方法,它通過對串聯關節依次建立坐標系,利用機器人正、逆運動學中變換矩陣、逆矩陣連乘即可求解。我們發現任意不同自由度機械臂關節旋轉平移矩陣相同,可設計算法統一來計算關節之間的關系,這樣可將設計理念快速實踐于初始參數與結果的驗證,重心轉移到建模是否合理上。但多關節機械臂矩陣參數多,大幅度增加了其合理性驗證難度。人們往往通過matlab定義煩瑣變量實現矩陣轉換[3],過程較煩瑣。鑒于目前沒有成形算法來完成數、串混合的多參矩陣運算,本文主要解決機械臂基于字符多項式的矩陣、逆矩陣運算,實現一種快捷求解。
機械臂常見自由度有5、6、7三種。自由度越高,靈活度會越高,但其矩陣運算更加復雜。本文以KINOVAJac02球形7自由度臂為例,根據提供電氣參數實現算法,與其他自由度運算可通用。
1 機械臂運動學模型
以Denavit-Hartenberg表示法建模的機械臂,通過對各關節建立坐標系相鄰關節以齊次變換矩陣表示轉動和平移關系,依次矩陣連乘可確定基座與末端姿態的關系。其中每個連桿含長度a,扭角α,間距d,關節角度0四個參數。
1.1 正運動學模型
2 基于字符串的矩陣運算
字符串矩陣運算,先解決字符多項式四則運算,后進行矩陣運算。
2.1字符多項式四則運算
字符多項式由操作數和操作符組成,與常規代數多項式邏輯相同,只是符號不同。它既含數又有字符串,如(cosαsinβ*a)*(cosθ1+5),計算機無法區分cos、cosθ1、1中哪一個是“變量”。我們將構建一套基于人直覺思維模式的類專家系統,利用遵循約定俗成且符合人們直覺的規則,進行語義分析,從而有效識別字符多項式[6][7],為三角函數、矩陣、逆矩陣運算奠定基礎。
計算機多項式運算,通常有前綴表達式、中綴表達式和后綴表達式(又叫逆波蘭表達式)三種方法。逆波蘭表達法嘲,通過簡單人棧和出棧完成所有多層嵌套的四則運算,生成機器碼效率高,不但純數值運算方便,字符運算同樣出眾,故本文用該表達法實現。
為實現字符多項式運算,將基于常規邏輯的數值運算規則擴展到字符范疇,它們會在矩陣、三角函數反復用到,為此我們做如下主要約定:
Rulel-符號多項式轉換符號單項式規則
Rulel-I有效算符法則:①五種合理的組合映射:卜+,+一,一,++,++,(+,一(}->{-,+,+,+,*,(,-l*};②八種非法組合:(-*,+*,一),+),**,*),(),)();③三種非法頭算符:(*),+】;④四種非法尾算符:((,+,一,*】;
Rulel-2操作數分隔法則滿足rulel-1,對操作數“變量”分隔,做如下主要約定:
①長度為1的多項式合法,算式{-}>{1),其他算符非法,操作數合法;②介于兩個算符之間,提取字符串,視為操作數。
Rule2操作數對象化約定規則后綴表示法中無括號,但有“正”“負”字符串。逆波蘭的字符表達式構建如下對象:{Opd[01,02.,],Opt[+/一,+/_,,],len),其中len≥l。
Rule3字符多項式運算法則基于規則rulel、rule2,有如下主要約定:
①加法約定式a+式b;②減法約定式a+(一1)*(式b);③乘法約定同號為正,異號為負,以*拼接單項式“變量”;④替換約定矩陣中三角函數運算有冗余,替換如下:{^1*,*1$,*1*,+1*,一1*)一>{'',”,*,+,一),其中^表示頭,$代表尾部,下同。
字符多項式的四則運算大致流程如下:①利用rulel分隔多項式;②根據逆波蘭通用算法,分隔多項式,生成逆波蘭表達式;③利用rule2和rule3計算字符多項式,返回結果。
該算法實現了基于多“變量”的字符多項式運算。在機械臂矩陣轉換中,將反復用到。
2.2 基于規則的矩陣運算
矩陣相乘要滿足:矩陣A(M*K)和矩陣B(P*N),其中K=P。A*B記做C(M*N),
字符矩陣運算,“變量”為字符串,對結果做如下約定:
Rule4字符串矩陣處理約定①符號映射(一,^+一卜>{+一,一);
②消除零值{^_0*,^0*,*0*,*一0*,*-0$,*0$);③中間映射{^一1*,^1*1*1$,*1*}>{一,,*)
矩陣相乘機械臂運算時遵循rulel-rule4約定,能有效化簡結果。大致流程圖見圖1。
3 結果分析
機械臂D-H模型的正逆運動學求解核心是選擇合適關節的旋轉平移矩陣計算。為簡明驗證本文模塊算法,通過設定不同關節角θ,求解正運動學末端位姿T和隨機關節旋轉矩陣逆矩陣,與matlab做對比。式2中左上方3*3矩陣表示姿態,右上方3*1矩陣表示位置(ci為cosθi,Sl為sinθi,i=1-7),運行結果見圖2。
3.1與MATLAB對比測試
隨機選擇不同關節角,末端位姿對比見表1,逆矩陣(參數α= π/2.a=0.d=-dl ,θ= θl =ql)對比見表2。
通過對比發現,不管是輸人數值型參數生成旋轉矩陣求解,還是通過圖2結果代人參數求值,與MATLAB結果一致。同樣,隨機關節旋轉逆矩陣也一致,說明了本文算法的正確性。算法可用于自由度小于八的任意D-H建模正運動學和逆矩陣運算。
4 問題展望
本文由弱變量的j avascript腳本語言,結合HTML實現。將多項式運算從純數值擴展到字符多項式,通過類專家系統構建了任意字符多項式四則運算、矩陣相乘、求逆矩陣等模塊,實現了數值、三角函數、字符夾雜的多項式矩陣相乘、求逆矩陣運算。其界面簡潔、結果易讀,只需輸入模型參數,直接獲得運算結果,將繁化簡,解決了D-H建模時矩陣運算煩瑣問題,具有較高的實用性。生成模塊易擴展到多變量矩陣運算的相關領域。
參考文獻:
[1] Denavit J,Hartenberg R S.A kinematic notation for lower-pairmechanisms based on atrices[J].Trans.of the Asme.journal ofApplied Mechanics, 1955(22):215-221.
[2] Chen YH,Dong F H.Robotmachining:recent development andfuture research issues[J]. The Intemational Journal of Ad-vanced Manufacturing Technology, 2013, 66(9/10/11/12): 1489-1497.
[3]楊捷.基于Matlab的平面機構分析解析法[D].成都:西華大學,2013.
[4]李程程.七自由度機械臂控制系統設計與研究[D].南京:東南大學,2016.
[5]徐俊虎,欒楠,張詩雷,等.7自由度機械臂的運動學逆解與優化[J].機電一體化,2011,17(6):28-33.
[6] Floyd RW.Syntacticanalysis and operator precedence[Jl.Jour-nal of the ACM (JACM),1963,10(3):316-333.
[7] Aho A V,Johnson S C,Ullman J D.Deterministic parsing of am-biguousgrammars[J]. Communications of the ACM, 1975, 18(8):441-452.
[8](美)AlfredV.Aho.編譯原理[M].北京:機械工業出版社,2008.
【通聯編輯:光文玲】
作者簡介:焦培金(1981-),男,山東青島人,本科,實驗師,主要研究方向為計算機應用。

