電磁感應現象中力電綜合問題應用分析

黑龍江 陳洪剛

縱觀近幾年的高考試題發現，電磁感應中力電綜合性的題目常作為壓軸題出現，尤其是以“導軌+導體棒模型”為背景的題目，展示內容常以近代科技生活實際為情景，涉及電磁感應知識與力學知識，綜合考查學生對力學和電學基本理論規律及方法的靈活運用，這是計算題的命題趨勢，也是命題的熱點。下面根據自己多年的教學實際，談幾點應對破解此類問題的方法和思路。

一、電磁感應中的動力學問題

1.解決電磁感應中的動力學問題，一般思路是“先電后力”，具體思路如下，用“四步法”分析

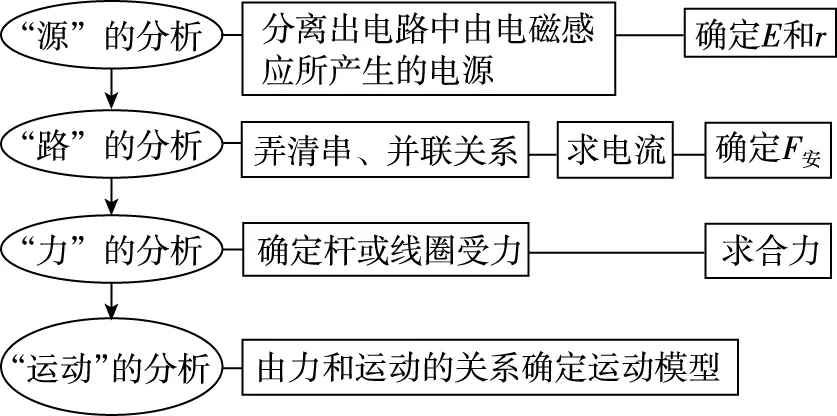
2.電磁感應中動態分析問題

在電磁感應中往往遇到“軌+棒”類問題，涉及動態分析，解決的基本思路是：先通過棒運動狀態的分析，尋找動態變化過程中的臨界狀態，如速度、加速度最大或最小的條件。具體思路如下：

【疑點解釋】

①對電源的理解：在電磁感應現象中，產生感應電動勢的那部分導體相當于電源，如切割磁感線的導體棒、內有磁通量變化的線圈等。

②對電路的理解：內電路是切割磁感線的導體或磁通量發生變化的線圈；除電源外其余部分是外電路，外電路由電阻、電容器等電學元件組成。在外電路中，電流從高電勢處流向低電勢處；在內電路中，電流則從低電勢處流向高電勢處。

【典例分析1】如圖1所示，P、Q為水平面內平行放置的光滑金屬長直導軌，間距為L1，處在豎直向下、磁感應強度大小為B1的勻強磁場中。一導體桿ef垂直于P、Q放在導軌上，在外力作用下向左做勻速直線運動，運動過程中，導體始終與導軌垂直并接觸良好。……