淺議質點組系統的機械能守恒解題分析

貴州 楊 勇

機械能守恒定律是解決動力學的基本定律，是自然界最普遍的一種能量守恒，機械能守恒的條件幾乎包括了功能關系的基本原理，機械能守恒的應用是動力學中的重點及難點，是高考考查的重點知識。所以理解和應用機械能守恒定律是高三復習的重點知識，由于多個物體系統的機械能守恒是多數學生在判斷和計算上容易出錯的問題，所以本文將從多個物體組成的系統進行分析機械能守恒定律的應用。

一、利用重心分析系統機械能守恒定律的應用

【例1】如圖1所示，AB為光滑的水平面，BC是傾角為θ的足夠長的光滑斜面，斜面體固定不動，AB、BC間用一小段光滑圓弧軌道相連，一條長為L的均勻柔軟鏈條開始是靜止地放在ABC表面上，其一端D至B的距離為L-a，現自由釋放鏈條，求當鏈條的D端滑到B點時鏈條的速率v。

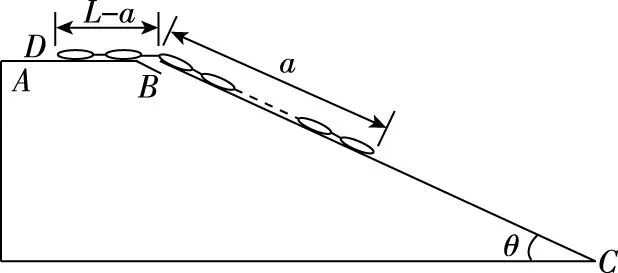
圖1

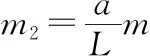
【評價】本題是考查學生對質量分布均勻的鏈條問題的處理，通常此類問題在考試中都以系統機械能守恒的形式出現，主要是考查學生對機械能守恒定律的理解和應用。但是對于此類問題，由于鏈條不是筆直的，所以在計算時，部分學生會把鏈條分成兩部分來計算，這樣鏈條和鏈條之間會有張力做功，導致計算錯誤，所以在練習時一定注意此類問題的系統性。

【變式1】如圖2所示，在傾角為θ的光滑固定斜面上，放有兩個質量分別為mA和mB的可視為質點的小球A和B兩球質量相等，兩球之間用一根長為L的輕桿相連，小球B距水平面的高度為h。……