教學(xué)考試雜志社“優(yōu)師計(jì)劃”階段性成果展示
——“電磁學(xué)”相關(guān)試題選登

一、電場(chǎng)

【例1】如圖所示，兩塊長度均為L的帶電平行板水平放置，兩板之間距離為d。當(dāng)兩平行板之間的電壓為U時(shí)，一帶電荷量為q的小球以速度v恰好能夠沿兩平行板之間的中心線做勻速直線運(yùn)動(dòng)，下列說法正確的是

( )

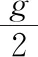
【例2】如圖所示的勻強(qiáng)電場(chǎng)中，A、B、C、D、E、F是一邊長為5 cm的正六邊形的頂點(diǎn)，已知A、C、D三點(diǎn)電勢(shì)分別為15 V、10 V、5 V。關(guān)于該勻強(qiáng)電場(chǎng)的場(chǎng)強(qiáng)，下列說法正確的有

( )

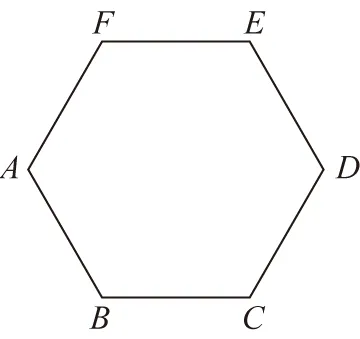
A.電場(chǎng)方向沿AD連線指向D，場(chǎng)強(qiáng)大小為100 V/m

B.電場(chǎng)方向沿AD連線指向A，場(chǎng)強(qiáng)大小為100 V/m

二、磁場(chǎng)

( )

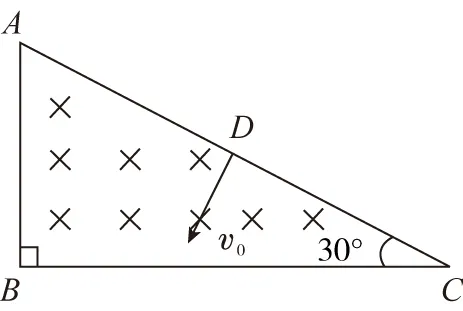
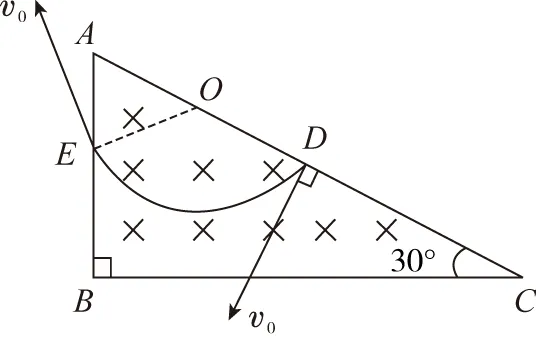
A.該帶電粒子帶負(fù)電

D.若將入射點(diǎn)D稍向A點(diǎn)移動(dòng)，其在磁場(chǎng)中運(yùn)動(dòng)的時(shí)間變長

( )

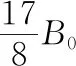
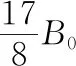
【例3】輕質(zhì)絕緣的細(xì)線一端連接固定的懸點(diǎn)O，另一端系在勻質(zhì)導(dǎo)體棒的重心(幾何中心)。假設(shè)導(dǎo)體棒垂直放在水平向左的勻強(qiáng)磁場(chǎng)中，電流向里保持不變，導(dǎo)體棒在重力、安培力的作用下正好保持平衡狀態(tài)，此位置細(xì)線水平，正好伸直但無拉力。現(xiàn)讓勻強(qiáng)磁場(chǎng)的方向沿逆時(shí)針緩慢轉(zhuǎn)動(dòng)，方向由水平向左緩慢變成水平向右，保持磁感應(yīng)強(qiáng)度的大小不變，在此過程中導(dǎo)體棒也緩慢的下降，懸線也緩慢的轉(zhuǎn)動(dòng)。認(rèn)為導(dǎo)體棒始終處于平衡狀態(tài)。有關(guān)懸線拉力的大小、方向的變化，下列說法正確的是

( )

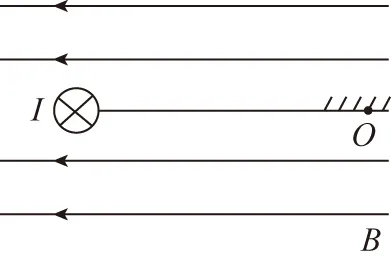
A.當(dāng)勻強(qiáng)磁場(chǎng)的方向沿逆時(shí)針緩慢旋轉(zhuǎn)的角度為α?xí)r，懸線繞O點(diǎn)旋轉(zhuǎn)的角度也為α

C.勻強(qiáng)磁場(chǎng)的方向沿逆時(shí)針由水平向左緩慢變成水平向右的過程中，懸線的拉力先變大后變小

D.勻強(qiáng)磁場(chǎng)的方向沿逆時(shí)針由水平向左緩慢變成水平向右的過程中，懸線的拉力不……