“編與分”：優化初中數學作業的實踐與評價

黃澤眾

摘要：從作業內容的設計，到作業結果的反饋，再到反饋評價的修訂，每一步都將影響作業“量”到“質”的轉變。新課標提出：“不同的人在數學得到不同的發展”，這一理念應當貫徹到數學作業這個環節中，應在減少學生作業負擔的同時，不影響作業的質量，并能發揮好作業的內在價值。因此，本文從“好題”的設計、分層作業的編排，對初中數學作業“量”與“質”進行探究，使得學生減負高效地對數學產生新的生機。

關鍵詞：數學作業；“好題”；分層作業；作業評價

中圖分類號：G633.6文獻標識碼：A文章編號：1992-7711（2020）04-0129

一、問題的提出

數學作業是數學學習中的一項重要內容，它不單是學生鞏固數學知識、形成數學解題能力的重要陣地，同時也是數學教師獲取信息的重要窗口。反思目前數學作業的現狀，大多采用“四統一”的方法，即統一題目、統一時間、統一上交、統一批改，學生的感受無疑是作業多、不會做，教師很難做到對所有的作業都精批細改，也無形中增加了教師的工作量，每天批改作業一般都是“√”“×”“？”或“閱”，最后形式化地給一個分數，學生不知所“錯”，收獲甚微。

二、問題分析

1.作業“教輔化”

在布置作業的過程中，教師會給全班學生統一布置教輔中的每節作業，從學生的作業質量上來看，存在著作業題和教材內容不匹配的問題，這就導致許多練習題都可能對學生并沒有直接的幫助，更為嚴重的是學生對考點的把握會出現分歧，花了許多精力去消化不是教學內容的知識點，作業反而變成了事倍功半的枷鎖。

如圖，在平面直角坐標系中，菱形OABC的頂點A在x軸正半軸上，頂點C的坐標為（4，3），D是拋物線y=-x2+6x上一點，且在x軸上方，則△BCD面積的最大值為______。

二次函數的幾何板塊并不是現在中考的考點，目前對于純二次函數考得比較多，所以本題二次函數與特殊四邊形的結合，不是十分符合當下學二次函數新課的作業，所以這種類似的作業對學生鞏固知識、加強二次函數的理解不會十分有效。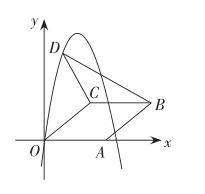

2.作業“繁重化”

教師為了提高學生的學習成績，尤其是數學這門學科，強化練習、不斷鞏固確實是可以提升學生的成績，但是從學生作業時間來看，回家作業上花費時間最長的科目就是數學學科，繁重的數學作業影響了學生各門學科的平衡。學生日常作業中的練習往往也存在著題目重復，相同題型反復做等現象，大大降低了學生學習數學的主觀能動性和積極性。

3.學生自信心低下

教師在批改作業中，經常只用“√“”×”“？”來進行批改，很多數學基礎薄弱的學生看到作業上批改的紅色的問號，慢慢積累后，作業上遺留的“？”不斷變多，會逐漸打擊學生學習數學的自信心，失去學習數學的興趣。

三、方法實施

1.編“好題”，體現作業含金量

（1）典型“好題”練重點

笛卡爾說過：“我所解決的每一個問題將成為一個范例，以用于解決其他問題。”學生學習時間寶貴，作業練習應當力求典型，具有代表性：既要鞏固應用當前所學知識、滲透重要數學思想方法，又要是某種規律的代表，能由“個”及“類”。

案例1：二次函數圖像及應用

如圖是一個橫斷面為拋物線形狀的拱橋，當水面寬（AB）為4m時，拱頂（拱橋洞的最高點）離水面2m。

①請你在右圖中，建立適當的平面直角坐標系，使得拋物線拱橋的函數關系式符合y=ax2+c（c≠0）的形式，并求出此時的函數關系式。

②當水面下降2.5m時，求水面的寬度。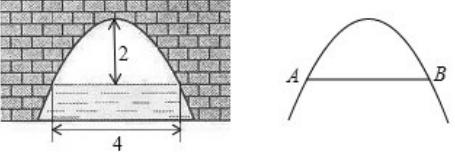

案例分析：這是一道數學書本中的原題變式，將本題通過拋物線的圖像出發，讓學生理解二次函數圖像本質的前提下，通過考查二次函數的對稱性建立坐標系，進行求解函數表達式。同時，通過水面下降2.5m，考查學生對題目的理解和二次函數圖像的應用。不僅考查了二次函數當下所學的性質，而且讓學生更明確地理解了二次函數的對稱性，有助于接下去的學習。

（2）同類“好題”尋關聯

量子理論創立者普朗克說：“科學是內在的統一體，它被分解為單獨的部門不是由于事物的本質，而是由于人類認識能力的局限，實際上存在著從物理學到化學、人類學到社會學的連續鏈條。”科學知識存在關聯，數學習題之間也存在聯系，比如二次函數與一元二次方程的聯系、數列規律中的用等，作業之間增強關聯性有利于學生站得更高、看得更遠、有利于學生把握問題本質。

（3）拓展“好題”常反思

有價值的作業，一方面可以通過典型題型、關聯性而加強學生對知識的整合、歸納與理解，引發學生主動反思。另一方面，為彌補初中生數學思維的局限性，設計一些反思性問題作為作業，可以以云圖的形式附在相應的習題旁，反思回顧解決問題的關鍵和解題思路，比如“運用兩點之間線段最短求最短距離”。

案例2：習題拓展課練習

題1：地下河兩側有村莊A、B，現要在河上方挖一口井向A村和B村供水，若要使得井口C分別到A、B兩村的水管之和最短，問井口C應在什么地方呢？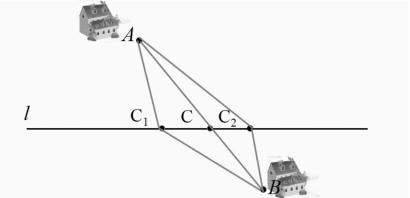

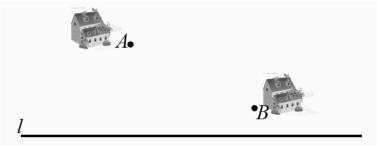
題2：如果當村莊A、B在河的同一側時，井口C又應在什么地方呢？

題3：如圖，在△ABC中，AB=BC=2，∠ABC=90°，E是AB邊上的中點，F是AC邊上的動點，求BF+EF的最小值。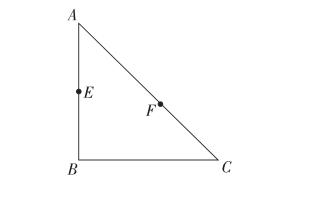

案例分析：按照上述題目的變式，根據數學的基本事實“兩點之間距離最短的”將數學作業進行關聯化，掌握一個定理，從而掌握一系列題型。這種系列性的作業可以幫助學生掌握一個知識點背后的變式，理解數學的本質，關注數學解題的思維。

2.分層次，設計作業合理性

統一要求的作業對優秀學生來說吃不飽，對一般學生來說剛“合胃口”吃得好，對學有困難的學生來說一定就吃不了，所以分層布置作業顯得格外重要。學生間的數學知識與能力的差異是客觀存在的，數學作業難度分層要針對不同層面的學生，改變統一要求，布置不同難度的課外作業，讓每一位學生都能經過自己的努力，“跳一跳”摘到自己所需的果子，都能體驗到作業成功的樂趣和自信。充分認識到數學作業的“質”。

筆者認為，數學教師能從浩如煙海的各種數學資料中為不同的學生精選出數學作業，并能適時適度的評價各種性質的作業，既體現了數學教師較深的功底，也是每一個數學教師必須研究的永恒課題。只有我們減少了無謂的數學作業量，提升了數學作業的質量，必定會煥發數學作業的活力，使學生將苦練變為樂做，由被動變為主動思考，才能實現真正意義上的減負高效。

（作者單位：浙江省杭州市保淑保塔申花實驗學校310012）