高考幾何光學中的常見模型分析

甘肅 張金龍 田生杰

光在玻璃磚中的折射和反射問題是高中物理光學部分的重點，也是高考考查的熱點，題型多以計算題的形式出現。這部分內容的難點是將光學問題與數學知識結合，體現了物理核心素養中的模型構建、科學推理及科學論證，要求學生能夠根據問題情景建立模型，運用全反射定律、折射定律和數學知識處理物理等問題。涉及的數學內容包括圓的知識、三角形知識、三角函數和正余弦定理等。

一、解題要點

1.求解光的折射、全反射問題的五點提醒

(1)光從一種介質斜射到另一種介質的分界面時同時發生折射和反射，如果光從光疏介質斜射入光密介質，則折射角小于入射角；如果光從光密介質斜射入光疏介質，則折射角大于入射角。

(2)光密介質和光疏介質是相對而言的。同一種介質，相對于其他不同的介質，可能是光密介質，也可能是光疏介質。

(3)如果光線是從光疏介質射入光密介質，則無論入射角多大，都不會發生全反射現象。

(4)折射現象中，光路是可逆的；光的反射和全反射現象，均遵循光的反射定律，光路均是可逆的。

(5)當光斜射到兩種介質的界面上時，往往同時發生光的折射和反射現象，但在全反射現象中，只發生反射，不發生折射。

2.應用光的折射定律解題的一般思路

(1)根據入射角、折射角及反射角之間的關系，作出完整的光路圖，注意入射角和折射角均以法線為標準。

(2)充分利用光路圖中的幾何關系，確定各角之間的關系，根據折射定律求解相關的物理量。

(3)注意在折射現象中，光路是可逆的。

3.解決全反射問題的一般步驟

(1)確定光是從光密介質射入光疏介質。

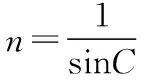
(3)根據題設條件，判斷光在傳播時是否發生全反射。

(4)如果發生全反射，畫出入射角等于臨界角時的臨界光路圖。

(5)運用幾何關系、三角函數關系以及反射定律等進行分析、判斷及運算來解決問題。

4.求解全反射現象中，光傳播時間問題的注意事項

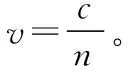
(2)全反射現象中，光的傳播路程l應結合光路圖和幾何關系進行確定。

二、光的折射、全反射模型分析

模型一 平行玻璃磚模型

平行玻璃磚模型是指兩個側面相互平行的玻璃磚或同種均勻介質，光路特點及對光線的作用如圖1所示，通過平行玻璃磚的光線不改變傳播方向，但要發生側移。

圖1

【注意】(1)側移距離的大小d與介質的折射率n、介質的厚度h及入射角θ1的大小等有關。

(2)根據光在折射過程中光路可逆，上述過程不可能發生全反射。

(3)應用本模型可以測定玻璃等介質的折射率。

【例1】如圖2所示，AB、CD分別是置于空氣中厚玻璃磚的上、下兩個表面，且AB∥CD，光線經AB表面射向玻璃磚，當折射光線射到CD表面上時，下列說法中正確的是

( )

①不可能發生全反射 ②只要適當增大入射角θ1，就可能在CD面上發生全反射 ③只要玻璃磚足夠厚，就可能在CD面上發生全反射 ④由于不知道玻璃的折射率，故無法判斷是否能在CD面發生全反射

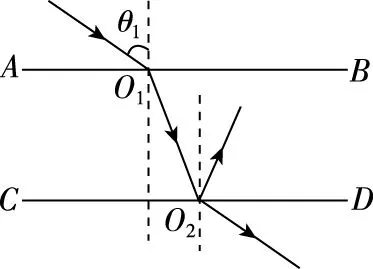
圖2

A.① B.②③ C.②③④ D.④

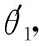
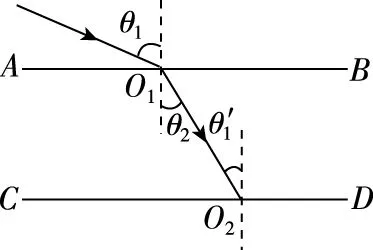
圖3

故折射光線O1O2在CD面上不能發生全反射，選項A正確。

【點評】本題考查光在平行玻璃磚中的傳播問題，根據折射定律和反射定律正確作出光路圖，再結合全反射的條件分析即可得出結果。當然本題也可直接利用模型一注意中第(2)條結論，光線通過平行玻璃磚的兩個平行側面過程中不可能發生全反射。

模型二 三角形玻璃磚模型

三角形玻璃磚模型(也稱三棱鏡)是指橫截面為三角形的玻璃磚，其橫截面可分為：一般三角形、直角三角形、等腰三角形、等邊三角形等多種。光路特點及對光線的作用如圖4所示，通過三棱鏡的光線經兩次折射后，出射光線向棱鏡底邊偏折。

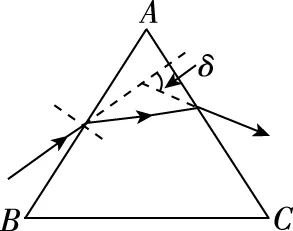
圖4

【注意】(1)調整入射角，光線在AC面的出射方向會改變，可能在AC面上發生全反射。

(2)兩種特殊入射方向①光線平行于BC邊入射；②光線垂直于AB邊入射。兩種情況光線在其他面上可能發生全反射。

(3)利用直角三角形或等腰三角形可制成全反射棱鏡，改變光的傳播方向。

【例2】如圖5所示，直角三角形ABC為一棱鏡的橫截面，∠A=90°，∠B=30°。一束光平行于底邊BC射到AB邊上并進入棱鏡，然后垂直于AC邊射出。求：(1)棱鏡的折射率；(2)保持AB邊上的入射點不變，逐漸減小入射角，直到BC邊上恰好有光射出，求此時AB邊上入射角的正弦值。

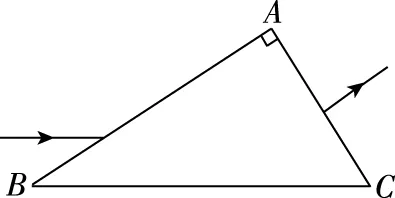
圖5

【解析】(1)光路圖及相關量如圖6所示。

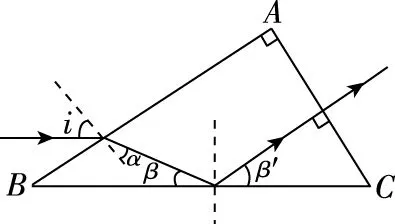
圖6

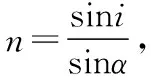
由幾何關系和反射定律得β=β′=30°

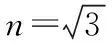
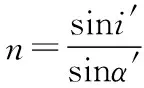
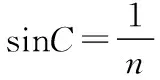
由幾何關系得C=α′+30°

【點評】1.本題是一道典型的直角三角形棱鏡模型問題，第一問根據光線沿平行三棱鏡的一個面這個特殊的方向射入棱鏡，求解折射率，第二問通過改變入射光的方向實現了在BC邊恰好發生全反射的臨界狀態。

2.題目考查光的折射定律和全反射定律，正確解題的關鍵是能夠準確作出光路圖，注意入射角、折射角均以法線為標準。

3.根據幾何關系尋找角度之間的關系，靈活運用數學公式sin(α-β)=sinαcosβ-cosαsinβ是快速求解的保證。

模型三 半球形(球形)或半圓形(圓形)玻璃磚模型

半圓形(球形)玻璃磚模型是指橫截面為半圓形的玻璃磚，光路特點及對光線的作用如圖7所示。

【注意】(1)光線沿球面斜射入，法線是過圓心的直線，經過兩次折射后向圓心方向偏折，由圓的幾何特性及光路可逆可知，光路不可能發生全反射現象，如圖7所示。

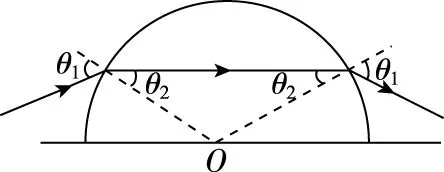
圖7

(2)光線沿半徑方向從球面射入，光線必經過球心，在直徑面上有可能發生全反射，如圖8所示；

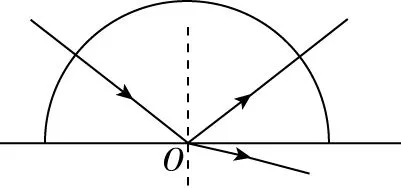
圖8

(3)光線沿與半球形直徑面垂直方向射入，由于入射點不同，在球面上可能發生全反射，法線為此點與球心的連線，如圖9所示。

(4)如果入射光線過半球形直徑面圓心，則折射光線必沿半球體半徑方向出射，如圖9所示。

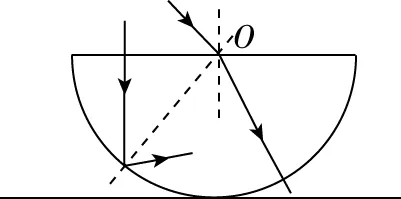
圖9

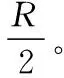
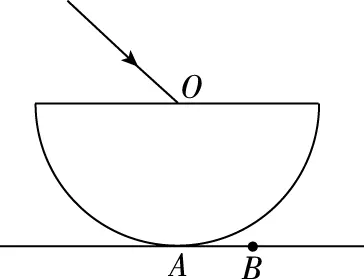
圖10

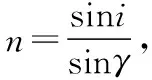
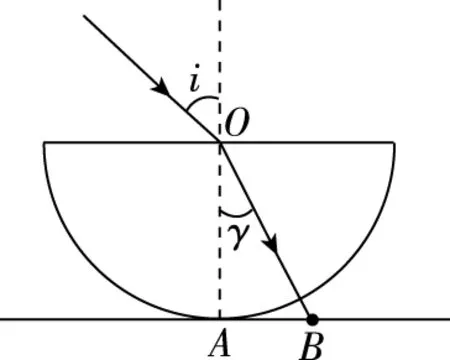
圖11

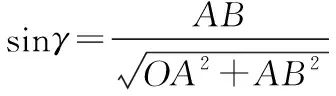
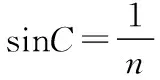
在玻璃體球面上光線恰好發生全反射時，光路圖如圖12所示。設此時光線入射點為E，折射光線射到玻璃體球面的D點。由題意可知∠EDO=C。

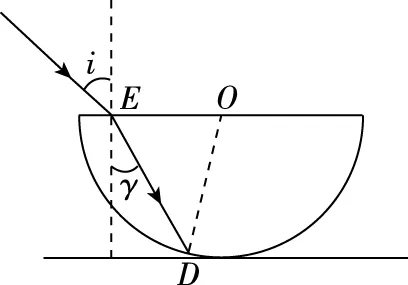
圖12

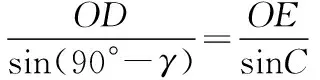
【點評】1.本題是典型的半球體模型問題，考查光的折射定律和全反射定律，難度適中。

2.題目描述的情景是入射光線過半球形直徑面圓心，同上文模型三中注意(4)，折射光線必沿半球體半徑方向出射的情況，當入射光線向左平移后，在半球面上發生全反射現象。

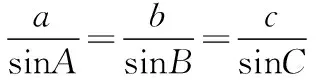
4.光線從半球體直徑面射入時，法線與直徑面垂直，光線射到半球體球面處時，法線過圓心沿半徑方向。

模型四 圓柱體模型

如圖13所示為圓柱體模型的橫截面圖，法線為過柱心的直線，如果光線垂直于圓柱體中心軸線沿半徑方向射入，則光線通過柱心不改變傳播方向；如圖14所示，如果光線以其他入射角沿截面射入圓柱體，光線向靠近柱心方向偏折；如圖15所示，如果光線垂直于圓柱體橫截面(沿圓柱體中心軸線方向)射入，則沿直線繼續傳播；如圖16所示，如果光線以其他角度射入圓柱體橫截面，則在橫截面處發生折射現象，在圓柱體內壁處可能發生全反射現象。

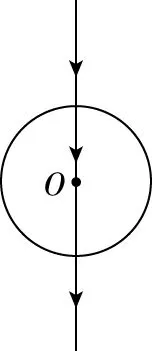
圖13

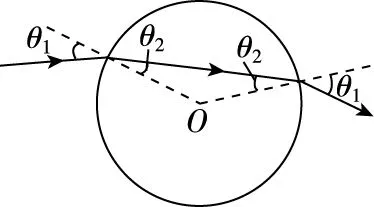
圖14

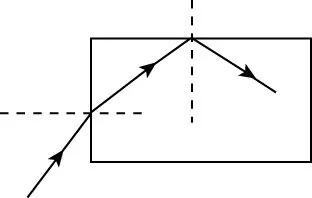
圖16

【例4】如圖17所示為一光導纖維(可簡化為一長玻璃絲柱體)的示意圖，玻璃絲長為L，折射率為n，AB代表端面。已知光在真空中的傳播速度為c。求：(1)為使光線能從玻璃絲的AB端面傳播到另一端面，求光線在端面AB上的入射角應滿足的條件；(2)光線從玻璃絲的AB端面傳播到另一端面所需的最長時間。

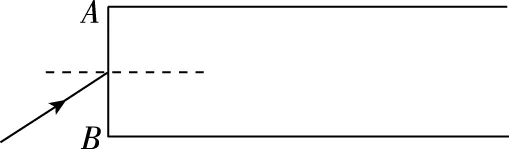
圖17

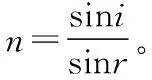
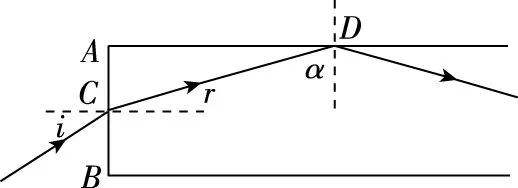
圖18

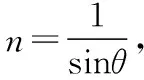
光速在玻璃絲軸線上的分量為vx=vsinα

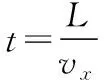
【點評】1.本題是一道非常典型的光在均勻介質中傳播的實際應用問題，屬于圓柱體模型問題，考查光的折射定律、反射定律及全反射知識，考查應用數學知識處理物理問題的能力，難度適中。

2.解答本題須了解要使光線能夠在玻璃絲中傳播，光線在玻璃絲內壁處能夠發生全反射，入射角應大于等于臨界角。

模型五 其他不規則形狀的模型

高考幾何光學考題中不僅考查光在以上常見模型(介質均勻，形狀規則)中的傳播，還可能涉及其他模型(介質均勻，形狀不規則)。無論什么形狀的介質，光線傳播都遵循光的反射定律和折射定律，正確作出光路圖是解決問題的前提。

【例5】寶石因特殊的材質和獨特的形狀而閃閃發光，打磨某剖面如圖19所示的寶石時，必須將OP、OQ邊與軸線的夾角θ切割在θ1<θ<θ2的范圍內，才能使從MN邊垂直入射的光線在OP邊和OQ邊都發生全反射(僅考慮如圖19所示的光線第一次射到OP邊并反射到OQ邊后射向MN邊的情況)，則下列判斷正確的是

( )

圖19

A.若θ>θ2，光線一定在OP邊發生全反射

B.若θ>θ2，光線會從OQ邊射出

C.若θ1<45°<θ2且θ=45°，最終的出射光線將平行于入射光線

D.若θ<θ1，光線會在OP邊發生全反射

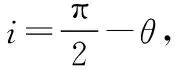
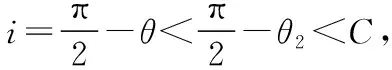
若θ1<45°<θ2且θ=45°，由幾何關系可知光線在OP、OQ邊會發生全反射，垂直MN射出，即出射光線將平行于入射光線，選項C正確。

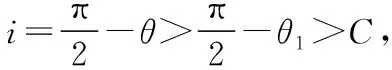
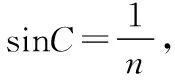
模型六 涉及長度、面積等照射范圍問題

涉及長度、面積等照射范圍的光學問題在高考中經常會出現，解題關鍵是運用動態的思維方式思考，確定臨界位置，在此基礎上確定光的傳播范圍。

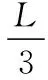
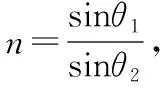
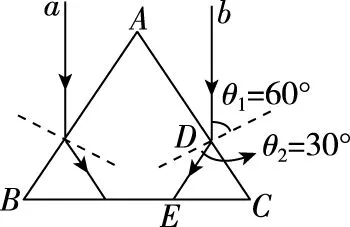
圖21

【點評】1.本題第(2)問要確定在桌面上形成的光斑面積，屬于確定照射范圍類問題，難度適中。

2.光束沿中心軸射入玻璃圓錐表面，進入玻璃發生折射現象，正確作出光路圖；確定邊界光線是解決本題的關鍵所在。

3.注意結合對稱性和幾何知識分析求解。

三、總結