數學核心素養在課堂教學中的滲透
——以《銳角的三角函數》為例

一、學情分析

本節課是章節的首要內容，是基于學生掌握三角形邊角關系、勾股定理等內容，進一步地展開關于直角三角形邊角關系教學。從核心素養的培養出發，九年級學生已經具有一定的類比和推理能力，需要讓學生在學習過程中注重觀察、猜想和類比，使其核心素養得到培養和發展。從課時性質角度來看，本節作為章節統領課，教師要讓學生形成概念的初步認知，使其能夠具備數學思維與能力。

二、教學目標

帶領學生認知直角三角形中銳角正弦函數的概念和意義，探索并學會求解銳角正弦值。在理解正弦函數的概念的過程中，體會函數運算思想；掌握并記憶學特殊角的正弦值，如30°、45°、60°，并能及時說出對應角度。通過建立由特殊到一般的過程，讓學生摸清并熟悉正弦函數概念的，體會數形結合思想的妙用。

三、教學重難點

重點：正確認知正弦函數概念，并學會求解銳角的正弦值。

難點：讓學生通過正弦函數概念摸清角度與數值間對應的函數關系，并熟練運用符號sin A 來表示函數。引入坡度、坡角等概念，讓學生將學習問題遷移實際問題中，使其能夠運用新知識解決坡角的簡單實際問題.

四、教學過程

1.場景先行，巧設疑問

問題1 老師導入了汽車爬坡場景，并引導大家思考坡度對汽車車速的影響

生1：坡度會減緩車速

生2：坡度越陡，汽車就不容易上去

教師：很好，大家知道什么是車的爬坡性能嗎? 我們又應該怎樣描述坡面的傾斜程度呢?

生3：在汽車滿載情況下，能夠越過的最大坡度就是爬坡能力。我們可以構建三角形，測量坡面和地平面之間的夾角(坡角)。

教師：這位同學指出了坡角的定義，并提出構建三角形來求坡角，那么大家猜想如何去求斜坡長度呢?

設計意圖：鑒于學生已經掌握直角三角形的基礎知識，教師借助情境引入環節，讓學生不自覺地思考直角三角形的邊角關系，使得初中數學知識的運用更具連續性。同時，通過情境引入和坡度坡角研究，激發學生探索坡角的好奇心，直指本節教學目的。

2.類比推理，學習新知

問題2 在求解前，老師帶領同學們判斷哪個斜坡更陡?

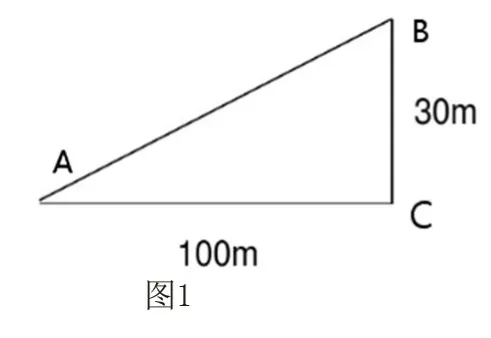
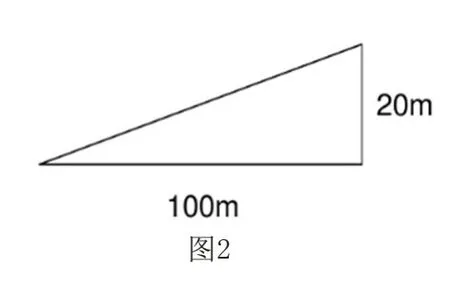
生1：圖1 更陡，地平面長度相等，高度不同可以判斷得出

教師：若圖1 構建的三角形為Rt△ABC，∠C=90°，∠A=30°，那么斜坡AB 長度為多少?

可求得，AB=60m

教師：若題目條件不變，當BC 為20，40，60 時，斜坡AB 為多少呢? 大家在計算中有何猜想?

生3：當銳角為30°時，不論直角三角形如何變化，∠A 與斜邊之比都為固定值。

教師：那么當銳角為45°時，這一關系會繼續保持嗎?

設計意圖：教師在這個環節中，運用幾何畫板進行動態演示，讓學生一邊觀察形象直觀的圖形，一邊在計算和類比中總結，對結論有一個清晰的認知，使其學在不經意間抓住本節重難點。

3.協作探究，摸清本質

問題3 經過猜想、類比和計算，大家得出了答案了嗎?

生1：不論直角三僥幸大小如何變化，直角三角形內一直角為45°時，這個角對邊和斜邊之比均為

教師：很好，這一結論正是大家要學習的新概念——正弦函數。

生問：那我們應該如何定義和理解這一概念呢?

教師：在Rt△ABC 中，∠C=90°，可以將銳角A 對邊與斜邊的比稱作∠A 的正弦值(sin)，記作sin A，即sin。

教師：對于新概念，大家需要注意到sin A 并非表示“sin”乘以“A”，而是一個完整的符號，而且這一符號是表示比值，沒有單位。那么大家可以推斷出sin A 與A 的關系嗎?

生2：每一個銳角A，sin A 都有唯一對應的值，可以將sin A 看成A 的函數。

教師：很棒，說得很正確，下面我來出題考一考大家：

快問快答

(1)sin 30°+sin 35°=；

(2)若Rt△ABC 各邊擴大10 倍，那么sin A 如何變化?

設計意圖：以計算形式讓學生總結類比和推理過程，并清晰地看到結論的正確性，更好地吸收新知識、認知新概念。而“快問快答”環節更能夠檢驗學生學習成果，使其感受自身的進步，更促進學生反思與總結，教師也能夠觀察到學生對知識的理解和吸收狀況，以便調整教學和導入形式，使得因材施教落到實處。

五、教學反思

本節教學內容主要是研究直角三角形的邊角關系，通過教學過程，學生們能夠認識到銳角三角函數是邊與邊的比值，在學習中收獲了計算、類比和推理的快樂，掌握了數學學習的方法和路徑。在各個教學環節中，教師采用了問題化教學法和情境導入法，在激發學生學習熱情的同時，使其緊跟教師的引導思路，借助實際情境和圖形進行探究，學生非常活躍，保持著積極的學習態度，在無形中培養了自身的數學素養。