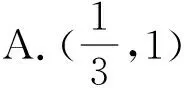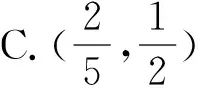基于核心素養的極限化解題認知活動設計

福建省漳浦第一中學 (363200) 蔡長寶閩南師范大學數學與統計學院 (363000) 林新建

“極限化”是重要的解題策略之一，它是用無限逼近的方式從有限中認識無限，從近似中認識精確，從量變中認識質變的思想.極限化方法在數學中有重要的應用，它能幫助我們快速地解決某些問題.對于越復雜的數學問題，其解題思路越有可能由“極限化”而輕松獲得.

“極限法好用，無限性難明”，學生為什么想不到運用如此簡便的方法予以求解呢？原因就在于他們無法感知出問題中蘊含的無限性特征，所以沒有辦法將問題解答得如此輕松.為此，教學中教師應認真設計“極限化”認知活動，讓學生經歷問題無限性特征的認知過程，這個認知過程至少應該包括：這是不是一個蘊含“無限性”特征的問題？這個“無限性”特征體現在哪里？這個“無限性”特征給你的啟示是什么？如何基于“無限性”特征將問題極限化予以求解？通過上述問題，學生充分經歷問題的感知、表征、結構分析、尋找策略、形成計劃、實施計劃等認知活動和反思總結等元認知活動，感知出問題內蘊的無限性特征，以此不僅輕松將問題解決，同時有效地培養和發展起數學的核心素養.

本文以全國卷高考試題為例，就極限化解題認知活動的設計在培養和發展數學核心素養上的意義與作用作一闡釋，以饗讀者.

1.設計“逼近性”認知活動，發展數學抽象、直觀想象素養

若問題中變量的取值具有逼近性的特征，即可無限逼近于某些值，則可運用極限方法將其極限化予以求解，可使問題獲得輕松解決.

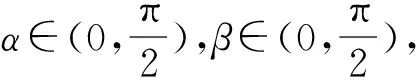
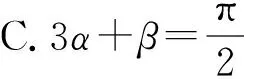
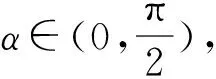
為此，教學中教師應認真設計“無限性”認知活動，讓學生經歷變量無限性特征的認知過程，這個認知過程至少應該包括：

問題1：由題設你能發現α與β的變化規律嗎？

問題2：這個變化規律是什么？給你什么啟示？

問題3：你能否根據這種啟示，將問題輕松予以求解呢？

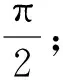
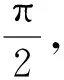
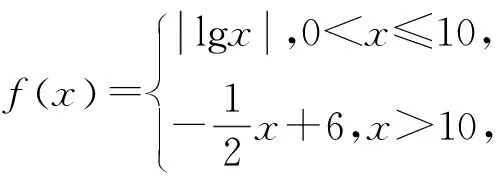
A．(1,10) B．(5，6) C．(10,12) D．(20,24)

解析：本題有一定難度，考生需要把握函數的圖形特征及變形技巧方能將問題有效解決.其實，若能運用極限化方法解決，問題可瞬間獲解，根本不用動筆.令a→1，則f(a)→0，f(b)=f(c)→0，從而b→1，c→12，abc→12，驗證選項即知正確答案為C.

為此，教學中教師應認真設計“極限化”解題認知活動，讓學生經歷無限性特征的認知過程，這個認知過程至少應該包括：

問題1：由題設你能發現變量a、b、c之間的關系嗎？

問題2：變量a、b、c的變化有規律嗎？這個規律是什么？

問題3：這個規律給你的啟示是什么？

問題4：你能否根據這種啟示，將問題輕松予以求解呢？

通過問題1，引領學生“從數量與數量關系中抽象出數學概念及概念之間的關系”，即a,b,c之間是有關系的，b、c隨著a的變化而變化；通過問題2，引領學生“從事物的具體背景中抽象出一般規律和結構”，即變量的變化具有無限性特征，變量a可無限趨近于0，也可無限趨近于1；通過問題3，引領學生“從一些事實和命題出發，依據邏輯規則推出一個命題”，即無限性問題可以極限化予以求解；通過問題4，引領學生“借助直觀感知事物的形態與變化，利用圖形理解和解決數學問題”，即令a→1，則b→1，c→12，由此知abc→12，驗證選項即知正確答案為C.

通過實施上述活動，學生充分經歷問題的感知、表征、結構分析、尋找策略、形成計劃、實施計劃等認知活動和反思總結等元認知活動，明了b、c隨著a的變化而變化，同時a可無限趨近于1，由此想到可將變量a極限化予以求解.

在以上活動中，學生“從數量與數量關系、圖形與圖形關系中抽象出變量與變量之間的關系，從事物的具體背景中抽象出一般規律和結構”，進而“借助直觀感知事物的位置關系、形態變化與運動規律，利用圖形理解和解決數學問題”，在這個過程中，無疑，數學抽象、直觀想象等核心素養得到了較好地培養和發展.

2.設計“趨向性”認知活動，發展邏輯推理、直觀想象素養

若問題中的參數具有變化的趨向性特征，即它的變化可趨于+∞，也可趨于-∞，則可運用極限方法將其極限化予以求解，可使問題獲得輕松解決.

例3 (2013年高考新課標卷Ⅱ理科12題)已知點A(-1,0)，B(1,0)，C(0,1)，直線y=ax+b(a>0)將△ABC分割為面積相等的兩部分，則b的取值范圍是( ).

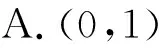
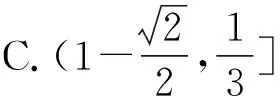
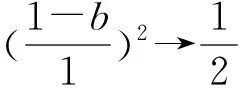
為此，教學中教師應認真設計“極限化”解題認知活動，讓學生經歷變量無限性特征的認知過程，這個認知過程至少應該包括：

問題1：由題設你能發現變量a的變化有規律嗎？

問題2：這個規律是什么？這個規律給你的啟示是什么？

問題3：你能否根據這種啟示，將問題輕松予以求解呢？

通過問題1，引領學生“從數量與數量關系中抽象出數學概念及概念之間的關系”，即a、b之間是有關系的，b隨著a的變化而變化；通過問題2，引領學生“從事物的具體背景中抽象出一般規律和結構”，即變量a的變化具有無限性特征，它可無限趨近于0，也可趨于+∞；通過問題3，引領學生“借助直觀感知事物的形態與變化，利用圖形理解和解決數學問題”，即令a→0與a→+∞求解問題.

通過實施上述活動，學生充分經歷問題的感知、表征、結構分析、尋找策略、形成計劃、實施計劃等認知活動和反思總結等元認知活動，明了變量a的變化具有無窮趨向性的特征，它可無限逼近于0，也可無窮趨于+∞，因此若運用極限方法予以求解，可輕松將問題予以解決.

在以上活動中，學生“從一些事實和命題出發，依據邏輯規則推出一個命題”，進而“借助直觀感知事物的位置關系、形態變化與運動規律，利用圖形理解和解決數學問題”，在這個過程中，無疑，邏輯推理、直觀想象等核心素養得到了較好地培養和發展.

3.設計“趨近性”認知活動，發展直觀想象、數學運算素養

若問題中動點具有運動的無限趨近性特征，即它的運動可無限趨近于某個點或某個位置，則可運用極限方法將其極限化予以求解，可使問題獲得輕松解決.

例4 (2003年全國卷理12題)已知長方形的四個頂點A(0,0)，B(2,0)，C(2,1)和D(0,1)，一質點從AB的中點P0沿與AB夾角為θ的方向射到BC上的點P1后，依次反射到CD、DA和AB上的點P2、P3和P4(入射角等于反射角).設P4的坐標為(x4,0).若1

為此，教學中教師應認真設計“極限化”解題認知活動，讓學生經歷動點的無限趨近性特征的認知過程，這個認知過程至少應該包括：

問題1：由題設你能發現動點P4的運動有規律嗎？

問題2：這個規律是什么？這個規律給你的啟示是什么？

問題3：你能否根據這種啟示，將問題輕松予以求解呢？

通過問題1，引領學生“從事物的具體背景中抽象出一般規律和結構”，即點P4的變化具有無限逼近性特征；通過問題2，引領學生“借助直觀感知事物的形態與變化，利用圖形理解和解決數學問題”，即點P4可無限趨近于P0，也可無限趨近于點B；通過問題3，引領學生“選擇運算方法，設計運算程序，求得運算結果”，即令P4→P0求解問題.

通過實施上述活動，學生充分經歷問題的感知、表征、結構分析、尋找策略、形成計劃、實施計劃等認知活動和反思總結等元認知活動，明了動點的運動具有無限趨近性的特征，它可無限趨近于P0，因此若運用極限方法予以求解，可瞬間將問題予以解決.

在這個活動過程中，學生“借助直觀感知事物的位置關系、形態變化與運動規律，利用圖形理解和解決數學問題”，進而“選擇運算方法，設計運算程序，求得運算結果”，將運算簡化到極致，無疑，直觀想象、數學運算等核心素養得到了較好地培養和發展.

數學素養是一種內在的思維品質和能力，它很難直接地被觀察，只有將這種內在的思維品質和能力轉化為外在的行為時，教師才能觀察到學生數學素養形成和發展的情況.教師在教學設計時，要將數學素養同具體的情境與問題相連，通過創設不同的模型認知活動，讓學生在日積月累的數學學習中，不斷地進行“數學認知”，積累數學活動的經驗，才能切實有效地培養起數學的核心素養.