例析均值換元法解數學競賽最值問題

江蘇省南京市第二十九中學致遠初級中學 (210029) 蔡俊劍

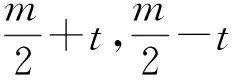
一、求最大值

例1(2016年全國初中數學聯賽初三年級試題)設實數x，y，z滿足x+y+z=1,則M=xy+2yz+3xz的最大值為( ).

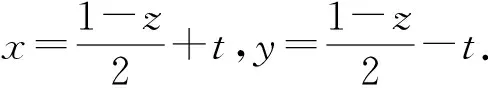
評注：本題依據已知條件x+y+z=1,M=xy+2yz+3xz,通過均值換元消去變量x，y，構造出一個關于t的一元二次方程，再利用方程有實數根的條件，“判別式大于或等于零”建立不等式求出M的最大值.解題過程巧妙自然，構思精彩，耐人回味.

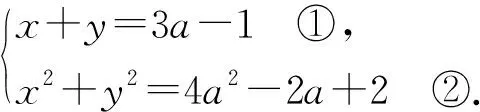
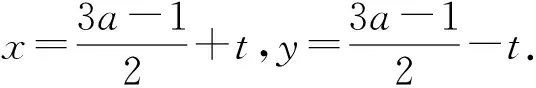
評注：根據題設巧用均值換元，再結合因式公解十字相乘法，通過解一元二次不等式求得a的取值范圍，然后再結合配方技巧求得xy的最大值.方法巧妙，解法新穎，匠心獨具，令人贊嘆.

二、求最小值

例3(2007年全國初中數學競賽試題)已知a+b=1，求a2+b2的最小值.

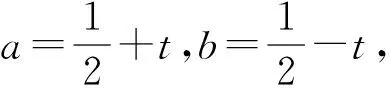
評注：本題運用均值代換，其絕妙之處在于能將多項式最值問題轉化為關于變量t的函數的最小值問題，從而只要令t2=0即可求得結果.其解法簡捷明晰，別具風味.

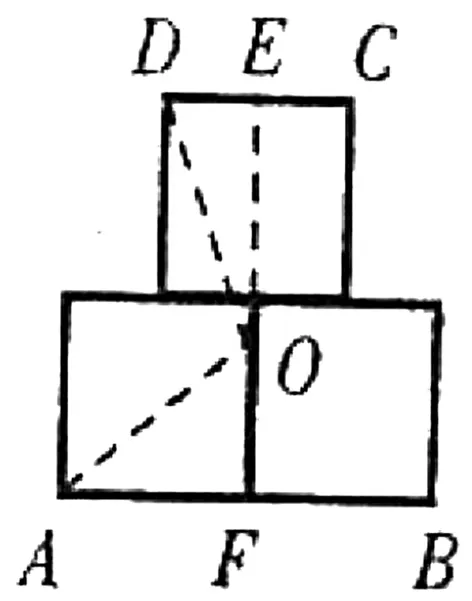
圖1

例4(2012年“希望杯”全國數學邀請賽初二第二試試題)如圖1，已知邊長為1的三個正方形排成一個“品”字，求覆蓋“品”字形的最小圓的面積.

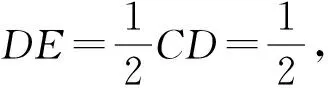
評注：本題的等量關系隱藏在圖形中，運用均值換元法，用平均數和一個字母表示圖中兩條線段的長，既形象直觀地表示出圓心的位置，又使計算簡單明晰，令人耳目一新.

三、求最大值和最小值

例5(2001年全國初中數學競賽題)已知實數a，b滿足a2+ab+b2=1,且t=ab-a2-b2.試求t的最大值和最小值.

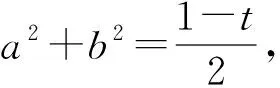
例6(2004年“信利杯”全國初中數學競賽題)設實數x，y，z滿足x+y+z=5,xy+yz+zx=3,試求z的最大值和最小值.

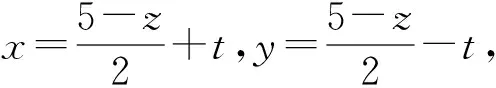
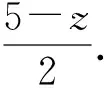
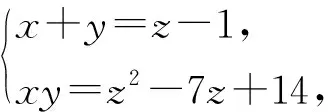
綜上可知，均值換元法的應用是極其廣泛的，方法通俗易懂，既有利于學生融會貫通“基礎知識和基本技能”，又有利于幫助學生提高綜合解題水平，對于啟迪學生思維、開闊學生視野，培養學生學數學、用數學、研究數學的興趣均頗有益處.