用基本不等式求最值的破題五措施

甘肅省武威第十八中學 (733000) 高述文

在運用基本不等式求最值時，要注意使用“一正、二定、三相等”條件，而在尋找定值時，有時條件不夠明顯，常需要采用拆項、添項、變形、化簡、換元等的技巧，這樣化隱為顯，使問題快速解決，本文通過舉例分析、介紹幾種常見的變換技巧，供參考．

1.適當拼湊：考察所給的表達式，看如何能通過進行適當的變形使之達到正確使用基本不等式的條件，完成解題目標．

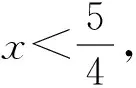
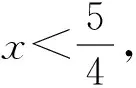
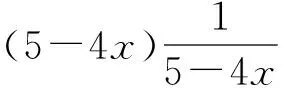
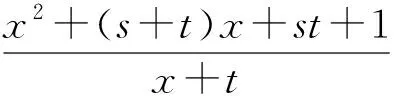
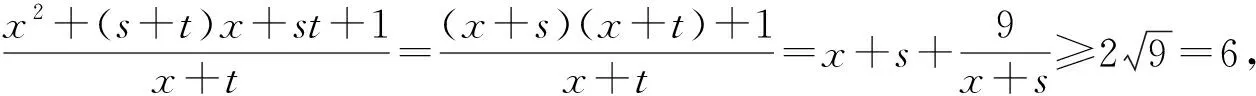
評注：本題容易出現誤判，即沒有抓住x+s>0進行正確的配湊，而是把x+t當著變元，使解題造成混亂得出錯解或使解題無法進行下去．

2.配方配項：在題設中如果在分式的分子或分母中含有類似于二式三項式的，可通過及時配成關于父母(或分子)的二式三項式，這樣后面的解題方法就能夠顯露出來了．

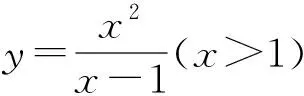
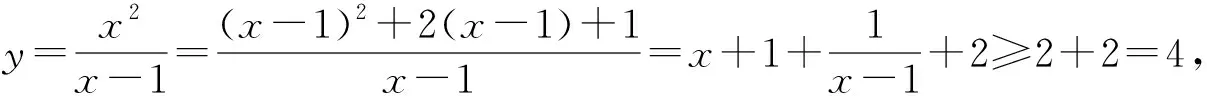
評注：在理解題意的基礎上，通過對分子配方(關于分母的平方)，構造出能使積為定值式子，這是找準了解題的切入點．

例4 若實數a、b滿足ab-4a-b+1=0(a>1)，求(a+1)(b+2)的最小值．

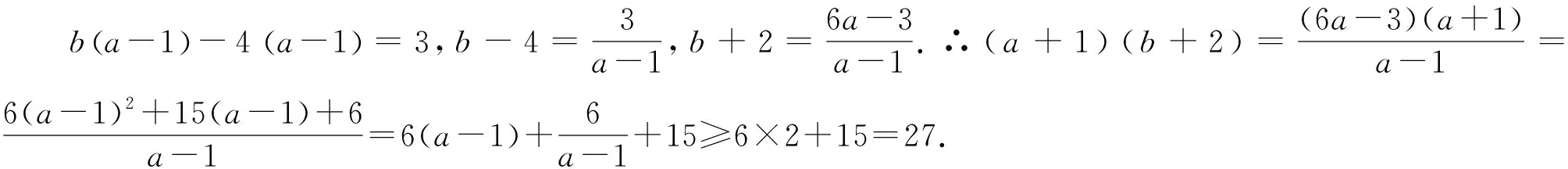
評注：本題中沒有直接告訴相關的分式，通過挖掘已知條件，對條件等式和欲求的式子進行重新整理，再合理配方，構造出可用均值不等式求解式子，化解了問題的難點．

3.及時相除：在一些分式求最值問題中，通過對分式的分子、分母同時除一個適當的式子，可以發現能使用基本不等式解題的契機．

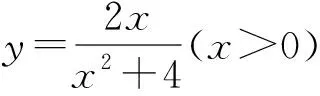
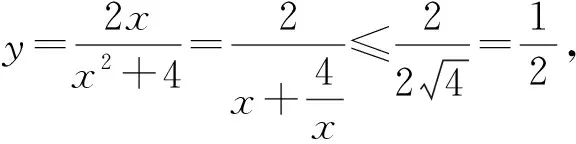
評注：通過分子、分母同除以x，使分子為常數(必須是)，同時也能使此時分母的積為定值，這樣就達到了使用基本不等式解題的條件了．

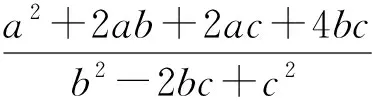
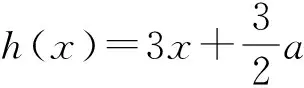
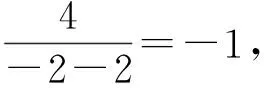
評注：通過對題目的深入研究，挖掘了其中隱含的關系，即一個乘積式的符合確定，再整體思考、整體變形配湊，使問題終于得到解決，這是科學有序的思維品質的體現．

4.連續放縮：在一些相對復雜的式子中，經過一次放縮可能達不到目的，可以再一次進行放縮變換，直到符合要求，這里必須注意連續放縮所需的相等條件是一致的．

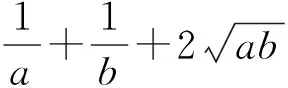
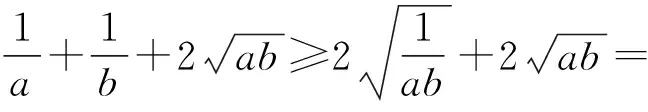
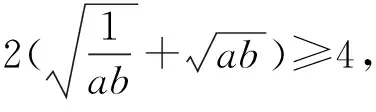
評注：本題雖然用了基本不等式放縮兩次，但由于等號成立的條件是一樣的且縮小的方向一致，故而并不影響最小值的確定，如果等號成立的條件不一樣或方向不一致，則得出的結果肯定是錯誤的，必須引起重視．

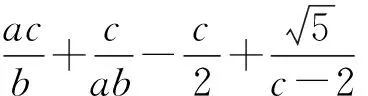
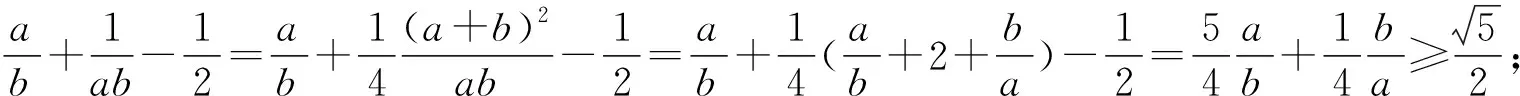
評注：本題中的字母較多，條件也不少，如何適當使用是解題關鍵，而本解法中分兩次運用基本不等式求解，方法獨到，簡便合理．

5.靈活換元：抓住題設中的某些特殊結構進行類比聯想，再通過換元對原式進行改造，可發現破題的機會，完成解題任務．

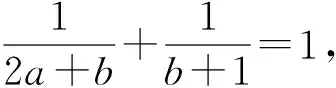
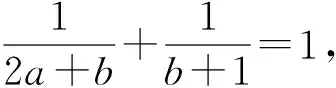
評注：若在題設中含有兩個正項和為1(或某個特定的值)，可以選用三角換元，這樣就可以利用三角函數的知識進行變形求解，達到解題目的．

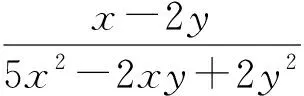
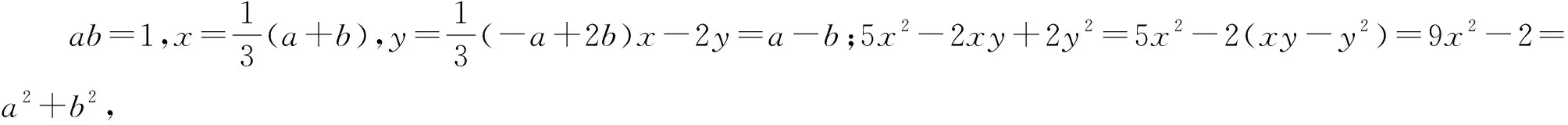
評注：本題通過對所給的式子進行變形，然后對其中的特定結構進行換元處理，用新變量替換原來的變量，揭露了隱含的關系，為順利解題創造了條件．

上面講述了使用基本不等式求最值的五個破題措施，常見而實用，如果我們在教學中能夠讓學生掌握并領會了這些解題方法，那么學生在應試時遇到這些題目可能就信心滿滿了．