高超聲速滑翔目標自適應跟蹤方法

黃景帥，李永遠，湯國建,*，包為民, 3

1. 國防科技大學 空天科學學院，長沙 410073 2. 中國運載火箭技術研究院，北京 100076 3. 中國航天科技集團有限公司，北京 100048

與傳統(tǒng)彈道式目標不同，高超聲速滑翔目標(Hypersonic Glide Target, HGT)具有大升阻比的氣動外形，在臨近空間以大于5的馬赫數飛行，依靠氣動力實現(xiàn)遠距離滑翔和大范圍機動[1]。隨著HGT相關技術日趨成熟，對該類目標的跟蹤引起了廣泛的關注，主要的難點在于較低的飛行高度降低了雷達可探測的時間、所建立的跟蹤模型難以囊括其復雜多變的機動模式[2-3]。

與跟蹤其他機動目標相比，跟蹤HGT存在一定的特殊性但也存在普遍性，相同的條件下量測傳感器精度完全由所建立的目標運動模型和采用的濾波算法決定，因此如何實現(xiàn)高精度的HGT跟蹤也是主要涉及這兩方面。目標運動模型用于表征目標的真實運動，特別是機動目標，濾波算法基于目標運動模型從噪聲量測中提取出目標的運動狀態(tài)。常用的運動模型包括常速度(Constant Velovity, CV)模型(屬于非機動模型)常加速度(Constant Acceleration, CA)模型、Singer模型、當前統(tǒng)計(Current Statistics, CS)模型、Jerk模型等，除了CV其他均屬于機動模型[4]。由于HGT依靠氣動力實施機動，因此氣動力加速度對于跟蹤系統(tǒng)來說是主要的未知輸入項，對其建模的優(yōu)劣一定程度上決定了目標運動模型的匹配性[5]。文獻[2]將HGT氣動力加速度中的未知氣動系數項建模成維納隨機過程，并擴展至系統(tǒng)狀態(tài)對其進行濾波估計，實現(xiàn)了穩(wěn)定跟蹤。文獻[6]中采用與文獻[2]中類似的建模方法，分別對HGT非跳躍式和跳躍式2種飛行軌跡進行了跟蹤濾波，發(fā)現(xiàn)當非跳躍式軌跡中的傾側角發(fā)生符號翻轉時由于目標運動模型匹配不及時會引起較大的估計誤差。文獻[3,7]進一步考慮了各氣動系數之間的耦合，給出了更加精確的氣動力加速度模型，但是需要一定先驗控制量的假設。上述模型均是從動力學的角度出發(fā)，對氣動力加速度進行精細建模，稱之為“動力學”模型。當然，從運動學的角度也可直接將HGT的加速度或氣動力加速度建模成已有的機動模型，但是與“動力學”模型相比通常缺乏理論根據性和清晰的物理意義，跟蹤精度對模型的參數較為敏感，需設置合適[6,8]。

由于HGT機動模式多樣，利用單一固定模型的適應性較差，難以獲得高精度的跟蹤，甚至針對HGT的某種機動形式現(xiàn)有的機動模型均不能較好地匹配，例如HGT為了調整側向運動會發(fā)生傾側角符號的切換[9]。文獻[10]基于非零均值正弦波相關模型對目標加速度進行均值補償和方差自適應，提高了跟蹤高超聲速跳躍滑翔式目標時的模型適應性。文獻[11]在認為控制變量服從一階時滯過程的前提下，實現(xiàn)了氣動參數模型與飛行狀態(tài)的自適應匹配，仿真結果表明當HGT目標發(fā)生機動時所提模型的跟蹤性能明顯優(yōu)于傳統(tǒng)模型。文獻[6]利用具有不同機動頻率的CS模型構成的交互式多模型(Interacting Multiple Model, IMM)對HGT進行跟蹤，并對目標氣動力加速度方差進行自適應調整，估計精度優(yōu)于傳統(tǒng)的CS模型。文獻[12]設計了一種自適應變結構的IMM算法用于跟蹤HGT，提高了跟蹤精度和效率。上述基于自適應模型的跟蹤方法通常需要一定的假設條件，其普適性和準確性有待商榷，難以實用；而多模型方法中由于缺乏可靠先驗信息使模型集個數和模型轉移概率難以確定，模型集過少不能全面地表征目標的運動，模型集冗余會增加計算量、引起模型間的競爭，跟蹤精度甚至得不到提升。此外，在跟蹤HGT的仿真驗證時，被跟蹤軌跡的設計大都未結合HGT實際可能采用的軌跡設計方法且未考慮完成制導任務的需求，致使跟蹤結果的可信度有所欠缺。

如前所述，目標跟蹤精度和濾波算法也緊密相關，相同目標運動模型采用不同的濾波算法通常會產生不同的估計精度，在目標跟蹤中自適應或魯棒的濾波方法已經廣泛地用于處理模型誤差。針對系統(tǒng)模型中未知的噪聲統(tǒng)計特性，提出了多種噪聲估計器，其中基于極大后驗準則的Sage-Husa估計器由于結構簡單、原理清晰得到了大量關注[13-15]。但是，文獻[16]指出Sage-Husa只有當過程噪聲或量測噪聲已知其中之一才是有效的。而且，引入估計器后易引起濾波的不收斂[17]。對于狀態(tài)模型誤差，基于正交性原理的強跟蹤濾波(Strong Tracking Filtering, STF)表現(xiàn)出較強的魯棒性，其通過漸消因子放大預測狀態(tài)誤差的協(xié)方差，強迫模型誤差出現(xiàn)時正交性原理依然能夠盡可能滿足，進而調整增益矩陣來增加新觀測數據的比重，以降低狀態(tài)估計誤差[18]。文獻[19]將STF用于跟蹤脈沖機動衛(wèi)星，可快速地降低脈沖機動引起的估計誤差，實現(xiàn)了高精度穩(wěn)定跟蹤。文獻[20]將STF應用至高階容積卡爾曼濾波(Kalman Filtering, KF)，增強了其跟蹤目標時的魯棒性。文獻[21]提出了一種歸一化的STF用于跟蹤小脈沖機動的航天器。由此，針對HGT運動模型誤差幾乎無法避免的情況，也可配合魯棒的濾波算法來提高跟蹤精度。

眾所周知，系統(tǒng)噪聲的統(tǒng)計特性對卡爾曼濾波結果的影響較大。上述所提跟蹤方法大多通過不同方式對系統(tǒng)過程噪聲的協(xié)方差實施自適應調整，最終提高跟蹤濾波精度。文獻[22]在跟蹤機動飛機時通過CS模型中的目標加速度遞歸方程和均值輸入估計方法提出了一種自適應CS模型，實現(xiàn)了對過程噪聲協(xié)方差的自適應調整。為解決跟蹤機動目標時Singer模型參數的失配問題，文獻[23]采用多模型方法中的似然函數并根據其變化自適應地調整最大加速度參數。對機動模型中的關鍵參數實施自適應調整的方法結構簡單、原理清晰，對跟蹤HGT具有一定借鑒意義。

為了提高HGT跟蹤方法的適應性和精度，本文在現(xiàn)有研究的基礎上提出了一種機動頻率自適應的跟蹤方法。首先將氣動力加速度建模成形式簡潔的Singer模型，基于正交性原理和無跡卡爾曼濾波算法利用濾波新息計算得到可反映狀態(tài)模型誤差大小的調整因子，然后用于放大Singer模型中的機動頻率參數，實現(xiàn)對當前模型誤差的自適應。仿真結果表明所提方法的適應性好、計算量小，能夠對HGT 2種典型的機動飛行軌跡實現(xiàn)高精度跟蹤。

1 目標跟蹤模型

目標跟蹤模型通常由狀態(tài)方程和量測方程組成，所建模型與目標真實運動模式的匹配程度直接影響著跟蹤精度。

1.1 狀態(tài)方程

圖1給出了HGT相對于地基雷達再入運動的示意圖，oxyz表示雷達坐標系，也即東北天坐標系。考慮地球旋轉，則HGT的相對運動方程可表示為

(1)

式中：δr/δt和δ2r/δt2分別為相對速度v和相對加速度；g和a分別為目標所受的引力加速度和氣動力加速度；ω和r分別為地球自轉角速度和目標地心矢徑；2ω×(δr/δt)和ω×(ω×r)分別為科式加速度項和牽連加速度項。

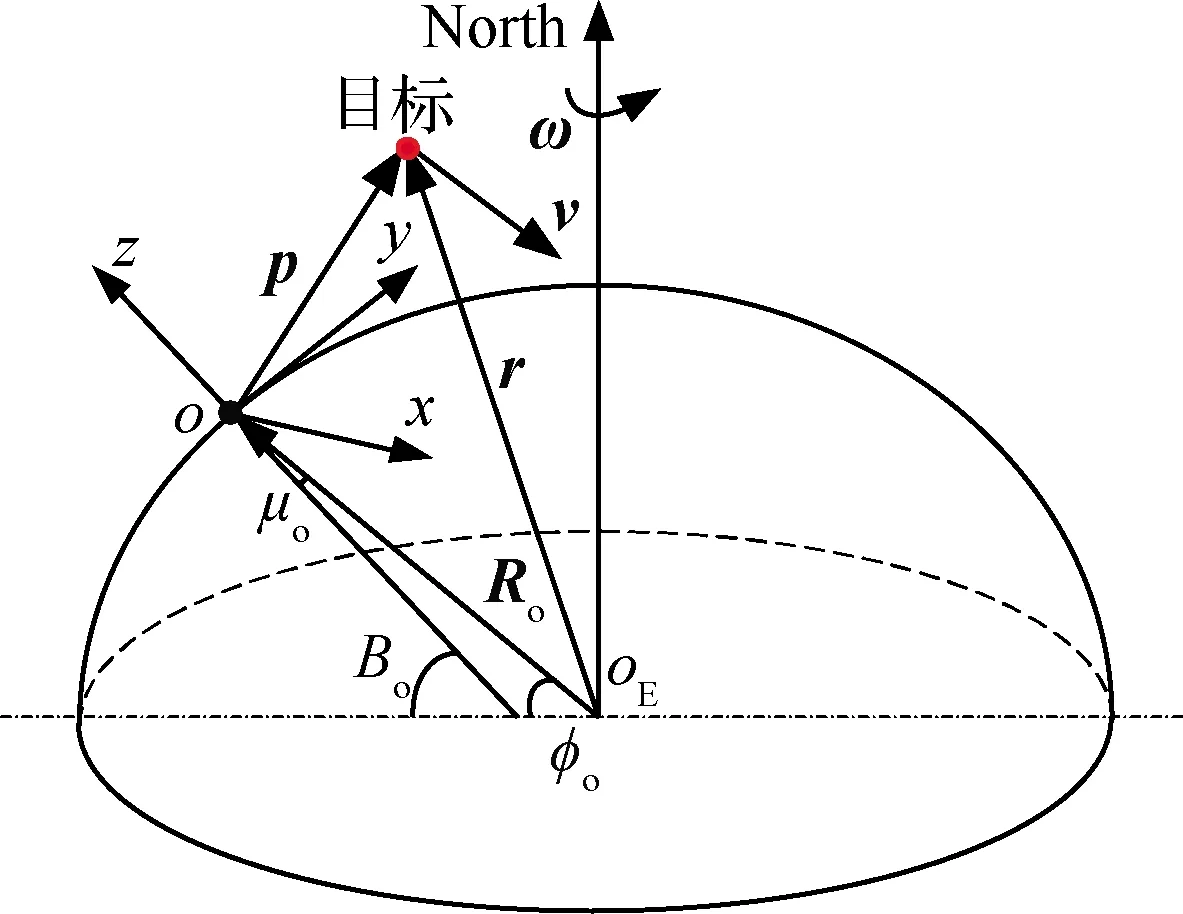
圖1 目標相對地基雷達的再入運動Fig.1 Target reentry motion relative to ground-based radar

為了獲得系統(tǒng)的狀態(tài)方程，需將式(1)投影至雷達坐標系下。設v=[vx,vy,vz]T，則相對加速度的各分量為

(2)

考慮橢圓地球，則引力加速度的形式為[24]

g=grr0+gωω0

(3)

式中：r0和ω0分別為r和ω方向上的單位矢量，其各分量分別為

(4)

其中：r為目標地心矢徑r的模;px、py和pz為p的3個分量;Ro為Ro的模；Bo為地理緯度;μo=Bo-φo，φo為地心緯度。gr和gω的表達式分別為

(5)

式中：μ為地球引力常數;J2為帶諧修正系數;aE為地球的長半軸。式(5)中，為了計算簡便近似地用地基雷達緯度φo替代目標緯度φ。

科式和牽連加速度項的表達式分別為

(6)

(7)

式中：r=[rx,ry,rz]T;ω為ω的模。

氣動力加速度作為HGT跟蹤系統(tǒng)中主要的未知輸入項，需進行重點考慮。這里直接從運動學的角度，將a建模成現(xiàn)有的機動模型。考慮HGT一直受到氣動力的作用，且機動強度有所起伏，選用介于CV模型和CA模型之間的Singer模型來匹配a的真實變化，因此有[4,25]

(8)

式中：λx、λy和λz分別為3個方向上的機動頻率；wx、wy和wz為互不相關的零均值高斯白噪聲，功率譜密度分別為2λxσ2、 2λyσ2和2λzσ2，σ2為當前時刻目標加速度的方差，表達式為

(9)

式中：amax為目標加速度的最大幅值，目標以amax或-amax實施機動的概率均為Pmax，P0為目標加速度為零的概率。

針對上述運動學建模，系統(tǒng)狀態(tài)方程可寫

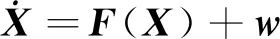
(10)

式中：X為系統(tǒng)狀態(tài)向量，具體表達式為

X=[px，py，pz，vx，vy，vz，ax，ay，az]T

(11)

F(X)的表達式見附錄A;w表示過程噪聲，為互不相關的零均值白噪聲向量，其自相關函數為

E[w(t1)wT(t2)]=Wδ(t1-t2)

(12)

式中：W為對角矩陣;δ(·)為狄拉克δ函數。

為了后續(xù)的濾波估計，需將式(10)進行離散化。設采樣周期為T，則式(10)轉化為

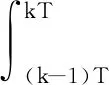
(13)

(14)

1.2 量測方程

地基雷達提供的量測量包括相對距離R、方位角A和高低角E，如圖2所示。

圖2 地基雷達量測量Fig.2 Ground-based rabar measurements

由圖2，易得量測方程為

(15)

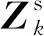
(16)

式中：p=[px，py，pz]T。

由于相對距離和角度之間的量級相差較大，為了降低濾波過程中出現(xiàn)矩陣條件數病態(tài)的可能性，將量測量轉換至直角坐標系下，可表示為

(17)

式中:Hk為系數矩陣。

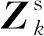
(18)

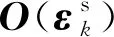
(19)

(20)

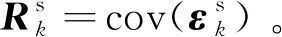
2 基于UKF算法的機動頻率自適應

鑒于HGT機動模式多樣，僅用單一固定的Singer模型難以表征氣動力加速度的變化。在卡爾曼濾波過程中，新息反映著系統(tǒng)模型所存在的誤差。假設量測方程準確的前提下，新息代表著狀態(tài)模型誤差，下面將其用于自適應Singer模型中的機動頻率參數。起始將式(8)中的機動頻率取至很小，此時Singer模型無限接近于CA模型，認為機動加速度變化平緩。當HGT機動加速度變化幅度增加時，放大機動頻率參數調整過程噪聲協(xié)方差。

由于狀態(tài)方程是非線性的，因此只能選用非線性的濾波算法。相比于擴展卡爾曼濾波(Extended KF, EKF)，基于無跡變換的UKF省去了復雜雅克比矩陣的運算，且具有更高的理論精度[26]。因此，選用UKF作為濾波估計的框架。

2.1 機動頻率自適應

對于線性KF，若系統(tǒng)模型能夠完全匹配真實模型，則濾波器輸出的新息序列滿足正交性原理，即[26]

(21)

式中：ξk為新息向量，即量測量與其預測值的差。當式(21)滿足時，意味著量測量中的有用信息被完全提取出來，因此新息序列的正交性可作為衡量濾波性能的標志。

對于次優(yōu)的非線性濾波器，新息序列不可能是完全正交的。此時若是弱自相關的，即可認為其具有較好的濾波性能。以EKF為例，考慮如下形式的非線性系統(tǒng)：

(22)

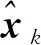
(23)

式中：Kk為濾波增益；Φk-1和Γk的表達式為

(24)

因此，對于EKF使新息正交性滿足的充分條件為

(25)

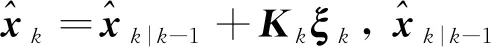
(26)

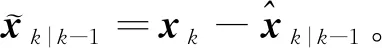
(27)

那么，量測量的預測值為

(28)

因此，ξk表示為

(29)

將式(29)和式(26)代入式(25)得

(30)

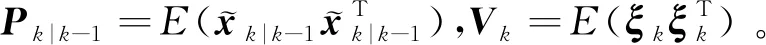
(31)

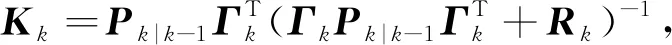
(32)

當狀態(tài)模型存在誤差時，會導致式(32)不再滿足，左右兩端不相等的程度反映著誤差的大小，并采用左右兩端主對線上元素的比值對其進行量化，具體形式為

(33)

式中：ζd稱為調整因子，反映了第d個量測通道上誤差大小。當目標進行大幅度機動引起狀態(tài)模型誤差時，可利用ζd對機動模型中的機動頻率實施相應調整，以降低模型誤差，提高濾波精度。當存在模型誤差時，Vk的真實值在實際計算中是未知的，可以通過式(34)對其進行估算：

(34)

式中：κ為遺忘因子，通常設置為0.95。

針對上述所建立的HGT跟蹤模型，量測量轉換后三通道上的調整因子可分別用于調整x、y和z方向上的機動頻率，x方向的調整策略為

(35)

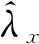
2.2 基于UKF算法的自適應實現(xiàn)

由于式(33)是基于EKF推導得出的，不能直接嵌入至UKF框架下，因此采用如式(36)所示的等效計算式：

(36)

式中：Py為依賴式(22)所描述的模型計算得到的新息協(xié)方差矩陣的標稱值，表達式為

(37)

對于式(22)所描述的非線性系統(tǒng)，首先對濾波器進行如式(38)的初始化：

(38)

自適應UKF算法可分為如下幾個步驟[26]：

1) 計算simga點和權重系數

(39)

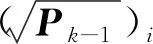
(40)

式中：β為與系統(tǒng)狀態(tài)先驗分布有關的常數，通常設為2。

2) 時間更新

(41)

(42)

3) 機動頻率自適應

(43)

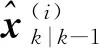
(44)

(45)

(46)

(47)

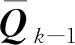
4) 量測更新

(48)

(49)

(50)

(51)

(52)

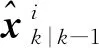
3 數值仿真

為了驗證所提方法跟蹤濾波的性能，首先設計2條典型HGT的飛行軌跡用于跟蹤，并與其他幾種跟蹤模型進行對比。

3.1 HGT軌跡設計

以美國洛馬公司發(fā)布的通用飛行器CAV-H模型為研究對象，分別基于阻力加速度-速度剖面跟蹤和高斯偽譜優(yōu)化方法生成2條再入飛行軌跡。考慮飛行過程中受多種約束的影響，主要設置最大過載為3g、最大動壓為100 kPa和最大駐點熱流密度為1 800 kW/m2，控制量攻角和傾側角的最大變化率分別為20 (°)/s和85 (°)/s，初終端的狀態(tài)約束如表1所示[12]。

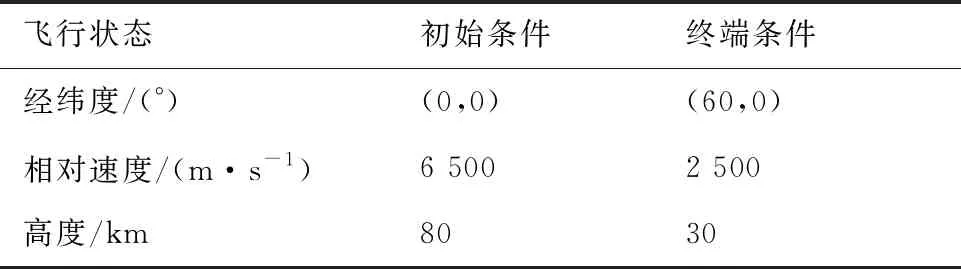
表1 CAV-H再入初終端條件[12]Table 1 Initial and terminal reentry conditions for CAV-H[12]

跟蹤阻力加速度-速度剖面是HGT再入段軌跡規(guī)劃與制導中常用的一種方法，其將再入段分為初始下降段和滑翔段，以是否滿足平衡滑翔條件為交班點，攻角剖面事先給定，初始下降段采用零傾側角飛行，在滑翔段跟蹤設計的阻力加速度-速度剖面用于控制縱向運動，由此確定傾側角的幅值，側向運動由視線方位角誤差走廊進行控制，用于確定傾側角符號的翻轉時機。以縱向跳躍幅度最小為性能指標，基于高斯偽譜方法進行軌跡優(yōu)化。具體兩軌跡的形態(tài)和狀態(tài)量的變化如圖3～圖5所示，“軌跡1”和“軌跡2”分別為基于跟蹤剖面和高斯偽譜方法獲得的軌跡。可看出，“軌跡1”存在傾側角符號的翻轉，會引起HGT的階躍機動，當傾側角不翻轉時機動較平緩；“軌跡2”的傾側角連續(xù)變化，機動幅度強于“軌跡1”中傾側角符號不翻轉時的幅度。上述2種典型軌跡可充分驗證跟蹤模型對不同機動模式的適應性。

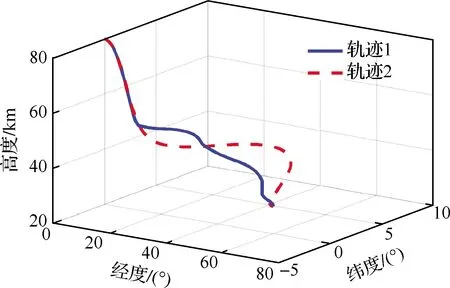
圖3 HGT跟蹤軌跡Fig.3 HGT trajectories to be tracked

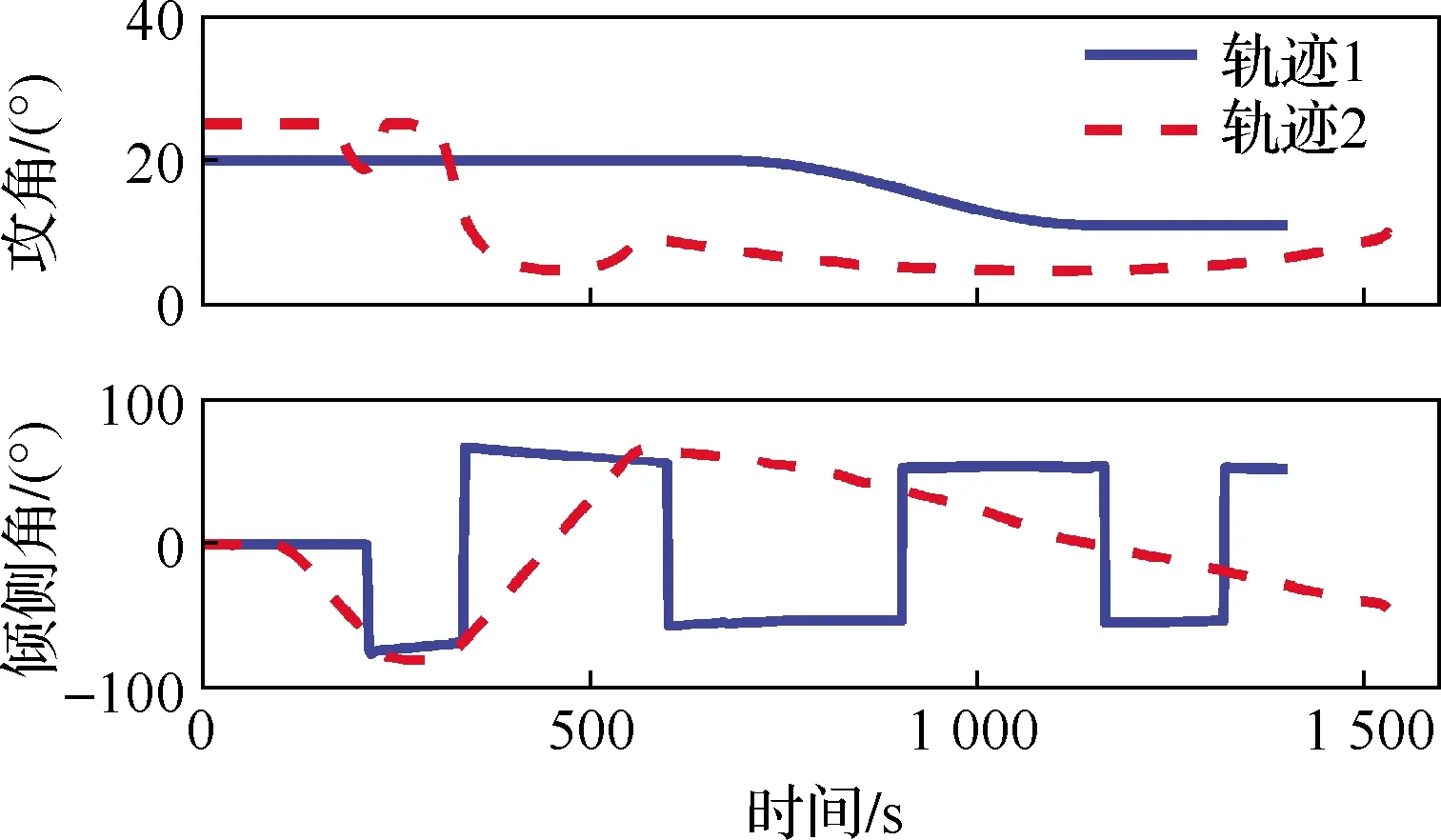
圖4 控制量隨時間變化Fig.4 Control variables versus time

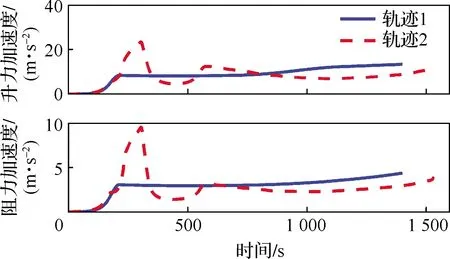
圖5 升阻加速度隨時間變化Fig.5 Lift and drag accelerations versus time

3.2 跟蹤濾波

為了充分地驗證所提機動頻率自適應方法的有效性，將其分別與基于Singer模型的方法、文獻[6]中提出的基于CS模型的方法、文獻[7]中提出的基于動力學模型的方法和文獻[6]中提出的利用IMM實現(xiàn)機動頻率自適應的方法進行性能對比。基于Singer模型的方法將氣動力加速度建模成Singer模型，如式(8)所示，基于動力學模型的方法見附錄B，基于CS模型的方法將氣動力加速度建模成CS模型，形式為[6]

(53)

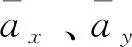
為了后續(xù)書寫方便，將基于Singer模型的方法簡記為“Singer”，在“Singer”基礎上引入自適應機動頻率的方法記為“Adaptive Singer”，基于動力學模型的方法記為“Dynamics”，基于CS模型的方法記為“Current Statistics”，圖6所示的基于IMM的方法記為“IMM-Singer”。為了保持仿真驗證的一致性，除“Adaptive Singer”中基于UKF算法對機動頻率進行自適應調整外，其他方法也均采用UKF算法。每種方法進行300次的蒙特卡羅仿真，采用均方根誤差(Root Mean Square Error, RMSE)來評估濾波結果的估計精度，位置RMSE的計算公式為

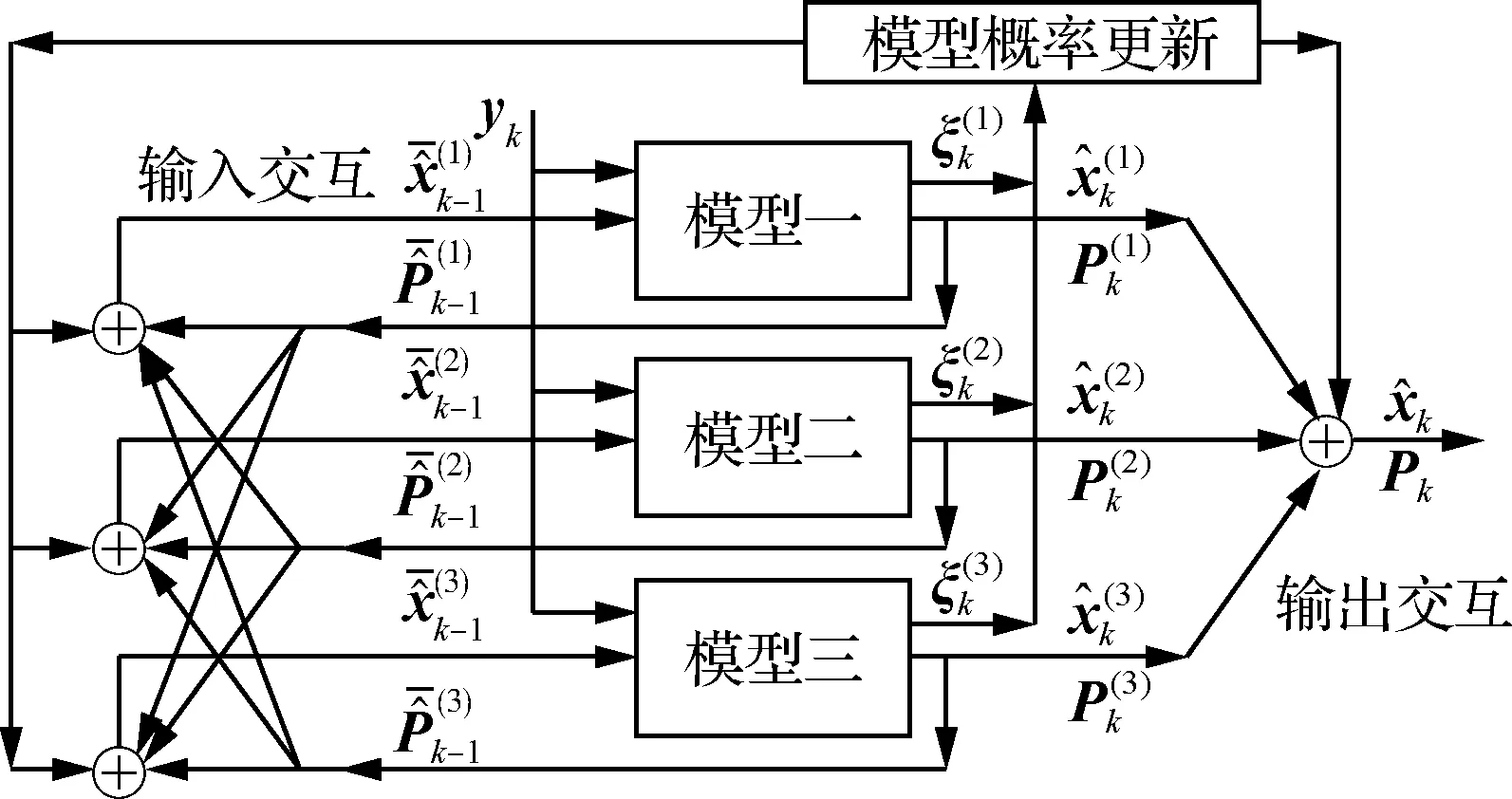
圖6 交互式多模型算法結構Fig.6 Structure of interacting multiple model algorithm

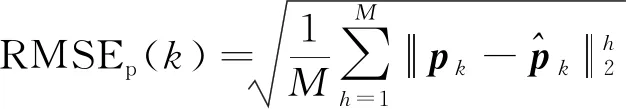
(54)

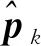
3.2.1 軌跡1

將雷達部署在經緯高為(35°, 0.5°, 0)的位置，設其最大量測距離為800 km。考慮地球曲率影響，易得雷達可量測的軌跡弧段及相應狀態(tài)量的變化，如圖7～圖9所示。由于圖4中t≈600 s時，傾側角發(fā)生了符號翻轉，相應地在圖9中引起了雷達坐標系下氣動力加速度的突變。

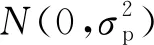
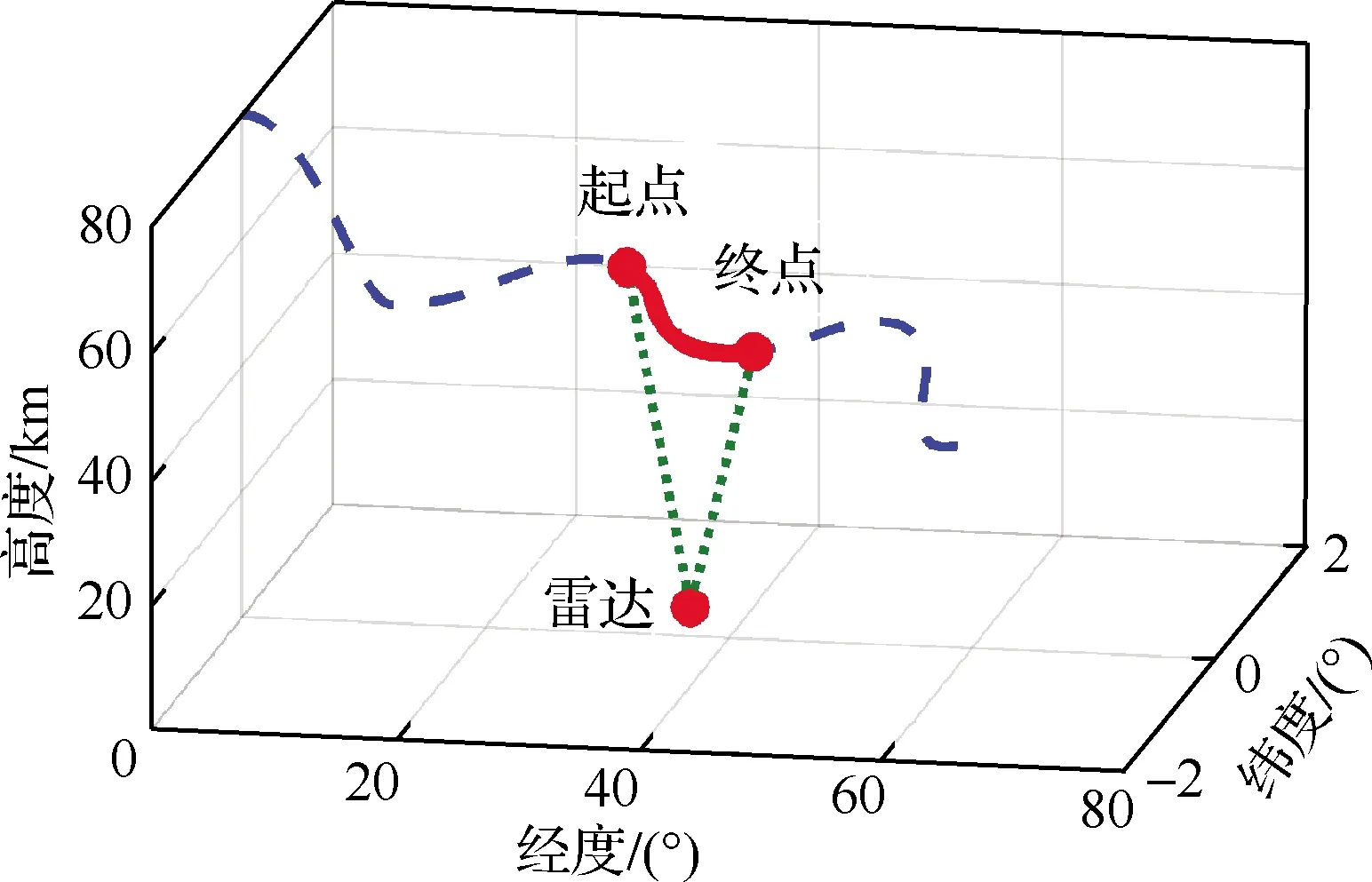
圖7 可觀測弧段(軌跡1)Fig.7 Observable segment (trajectory 1)

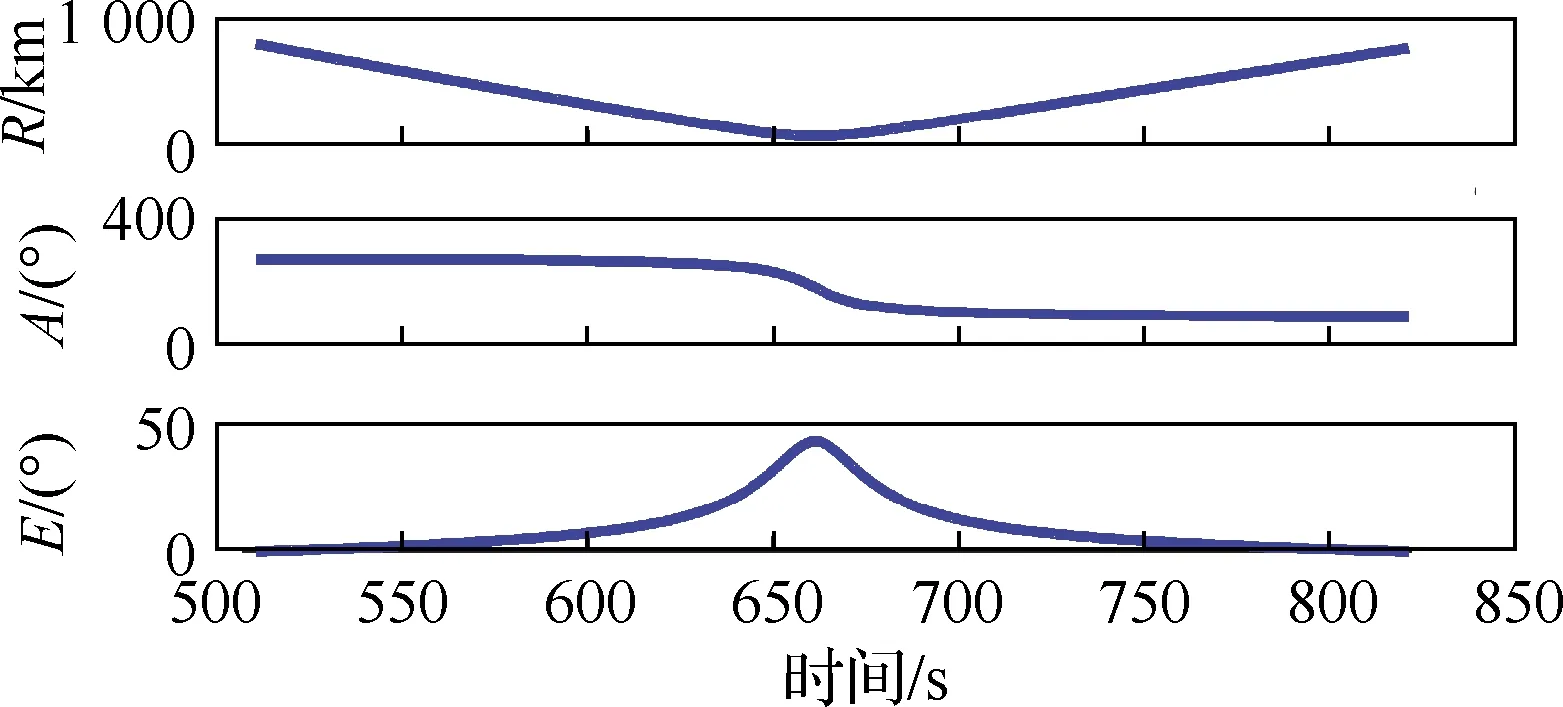
圖8 量測量真值(軌跡1)Fig.8 Noise-free measurements (trajectory 1)

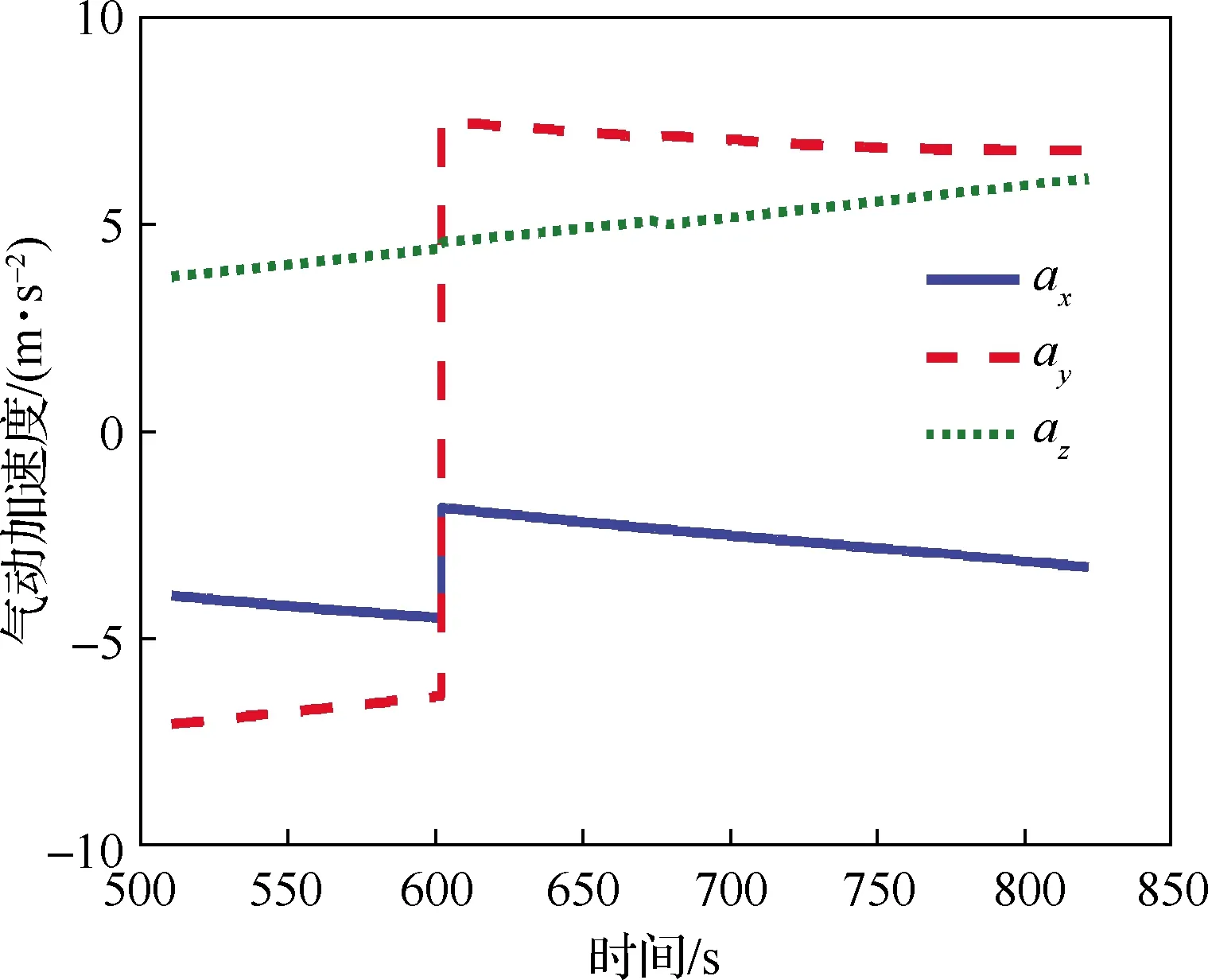
圖9 雷達坐標系下氣動力加速度真值(軌跡1)Fig.9 True aerodynamic accelerations in radar frame (trajectory 1)

(55)

式中：Λij為從模型i轉移到模型j的概率。

基于上述方法和仿真設置，分別進行300次的蒙特卡羅仿真，圖10～圖12給出了位置、速度和氣動力加速度的均方根誤差隨時間的變化。可看出，當氣動力加速度突變引起狀態(tài)模型誤差時，“Adaptive Singer”能夠快速地降低估計誤差，顯著優(yōu)于“Singer”，說明對自適應機動頻率的有效性。在700 s以后，目標機動幅值有變化但較平緩，該方法表現(xiàn)出輕微的自適應過度，導致精度略低于其他幾種方法，此時“Singer”和“Current Statistics”的精度稍高。“IMM-Singer”中由于采用IMM方法對機動頻率進行自適應，因此其估計精度與“Adaptive Singer”最為接近。“Current Statistics”理論上也具有噪聲方差的自適應能力，但是當加速度均值估計不準確時，可能適得其反，其結果劣于沒有自適應能力的“Singer”。“Dynamics”對HGT階躍機動的適應性最差。

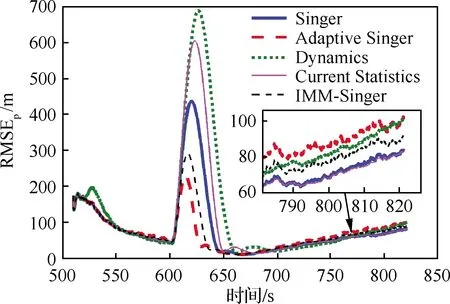
圖10 位置RMSE(軌跡1)Fig.10 RMSE of position (trajectory 1)

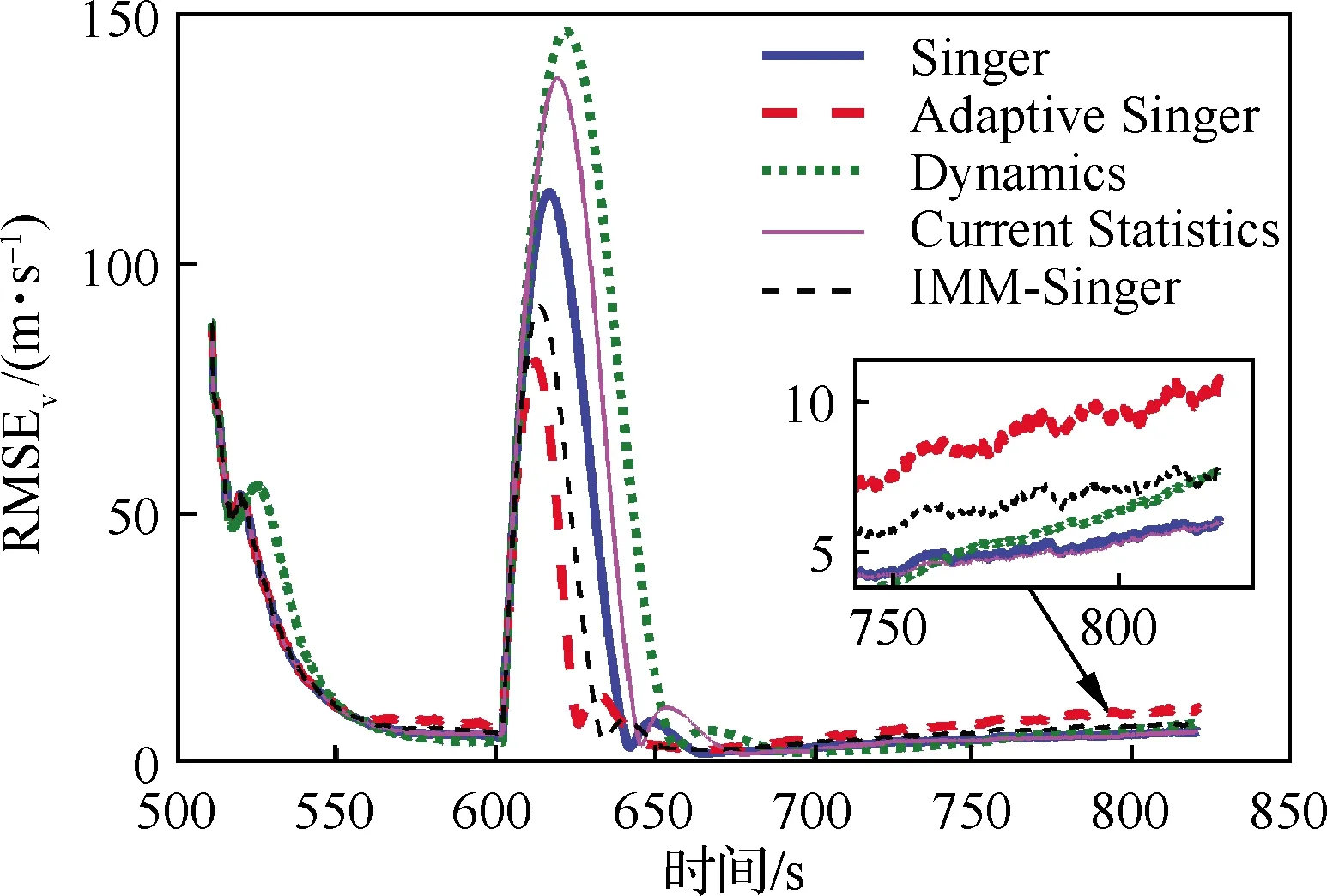
圖11 速度RMSE(軌跡1)Fig.11 RMSE of velocity (trajectory 1)

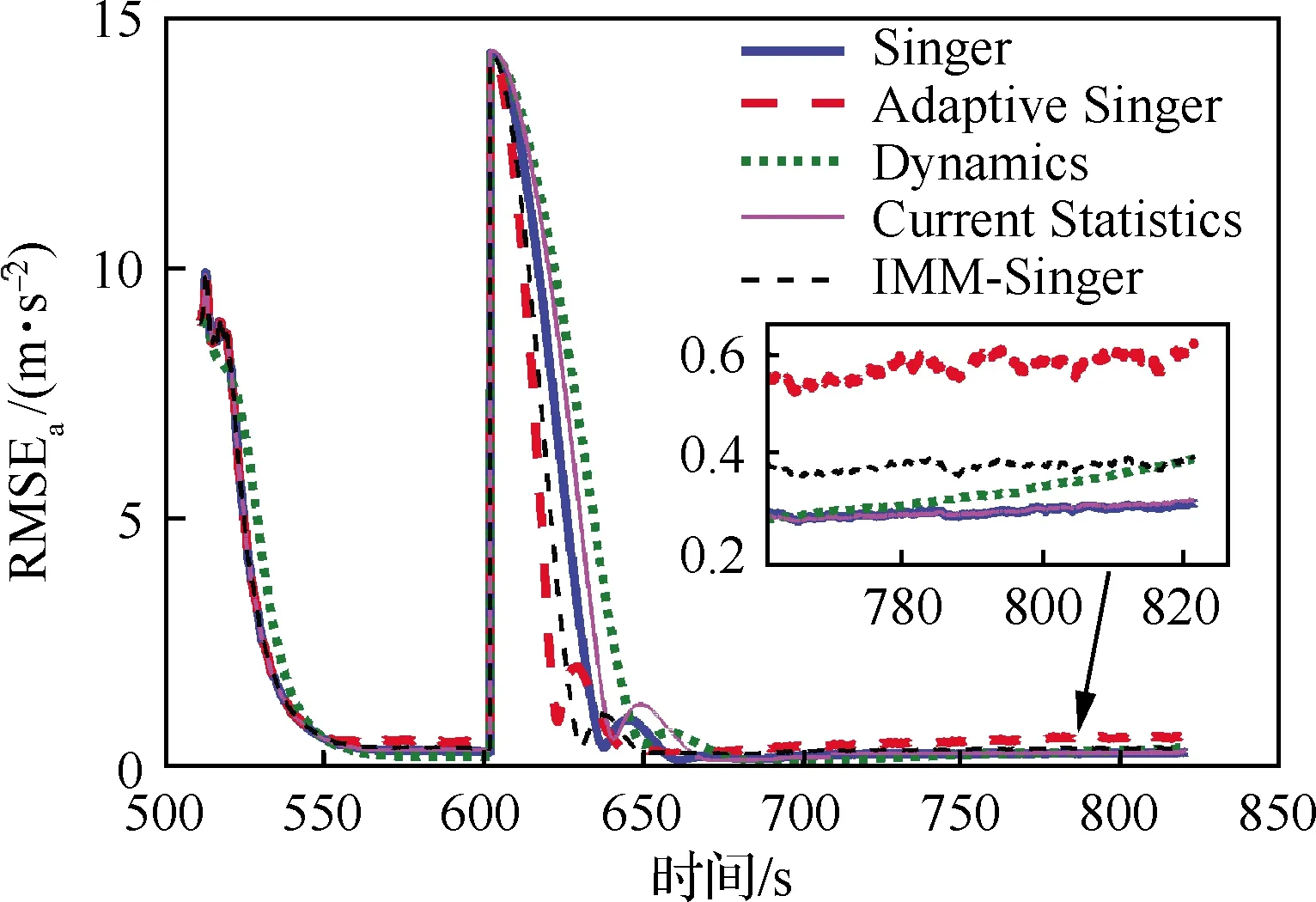
圖12 氣動力加速度RMSE(軌跡1)Fig.12 RMSE of aerodynamic acceleration (trajectory 1)

3.2.2 軌跡2

將雷達部署在經緯高為(23°, 5°, 0)的位置，與“軌跡1”相同，易得雷達可量測的軌跡弧段及相應狀態(tài)量的變化，如圖13～圖15所示。相比于軌跡1，軌跡2的機動是連續(xù)的，但是機動幅度的變化強于軌跡1無傾側角翻轉的時刻。

圖13 可觀測弧段(軌跡2)Fig.13 Observable segment (trajectory 2)

圖14 量測量真值(軌跡2)Fig.14 Noise-free measurements (trajectory 2)

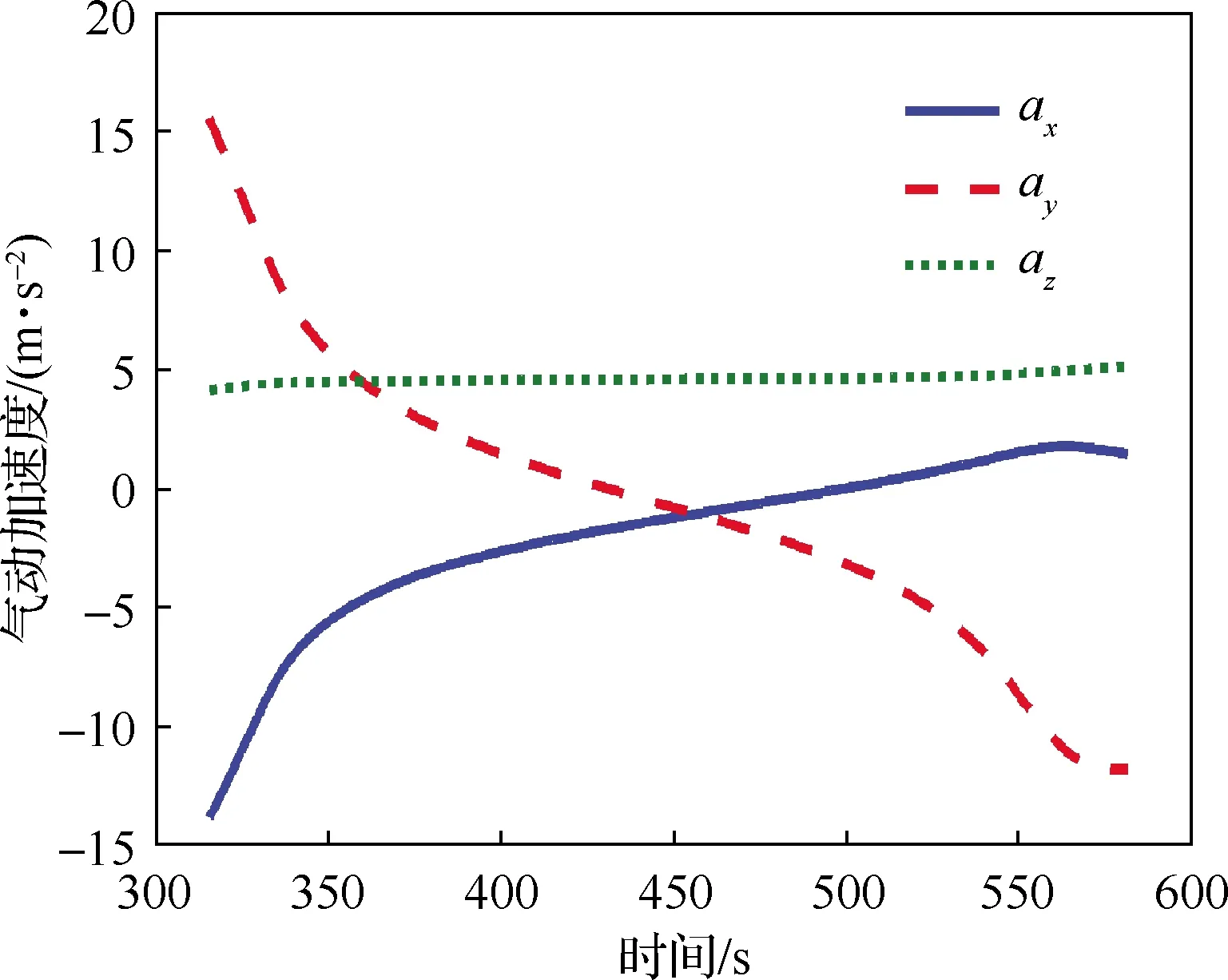
圖15 雷達坐標系下氣動力加速度真值(軌跡2)Fig.15 True aerodynamic accelerations in radar frame (trajectory 2)

為驗證各方法的適應性，仿真設置與軌跡1中保持一致，圖16～圖18給出了300次蒙特卡羅仿真后位置、速度和氣動力加速度的均方根誤差隨時間的變化。可看出，“Adaptive Singer”方法的濾波精度最高，對HGT機動幅度變化的適應性最好，特別是在目標機動幅度變化較大時，而“IMM-Singer”次之。由于機動幅度變化要強于軌跡一非階躍機動的時刻，導致其他幾種方法的估計精度較差，難以適應HGT多樣的機動模式。

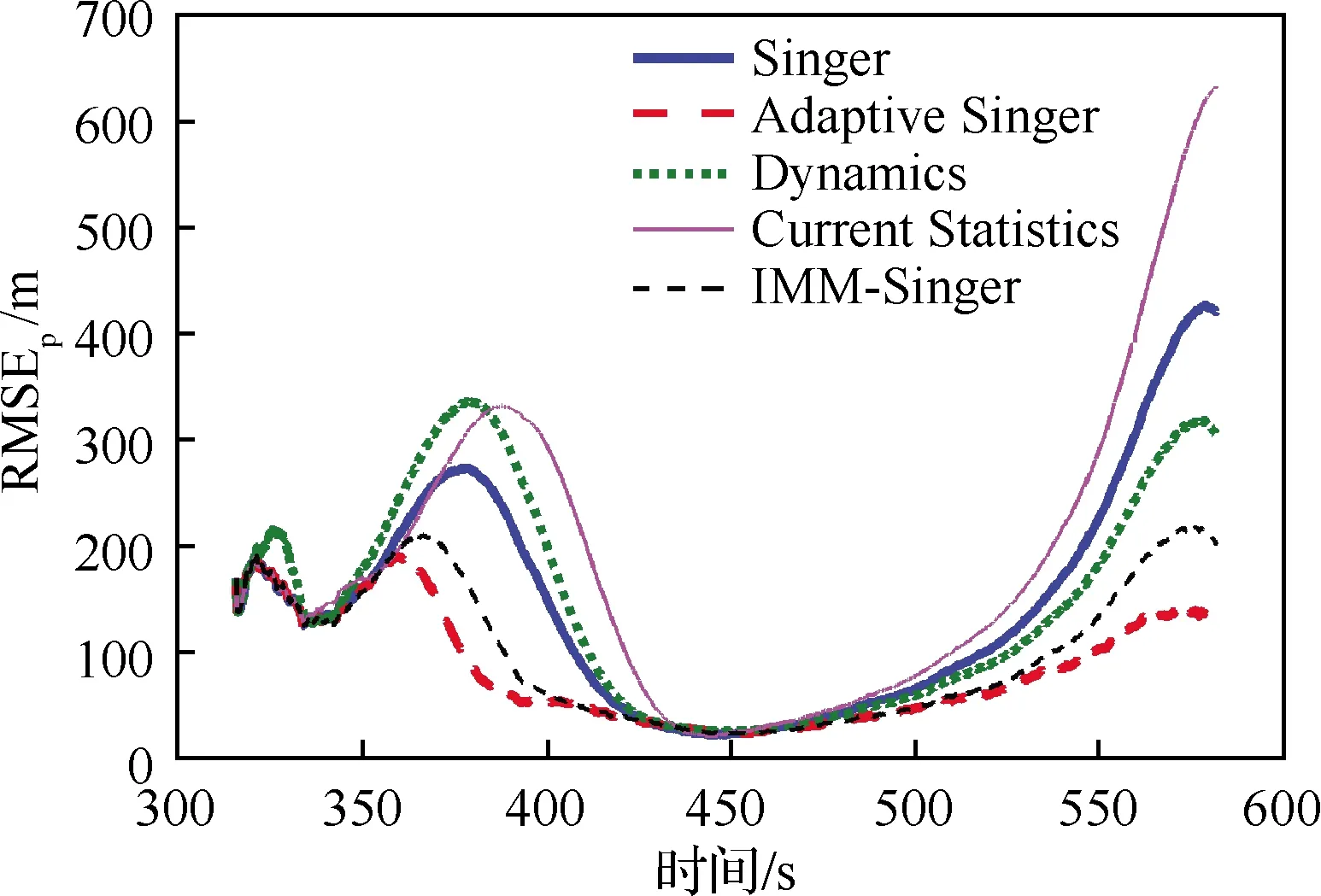
圖16 位置RMSE(軌跡2)Fig.16 RMSE of position (trajectory 2)

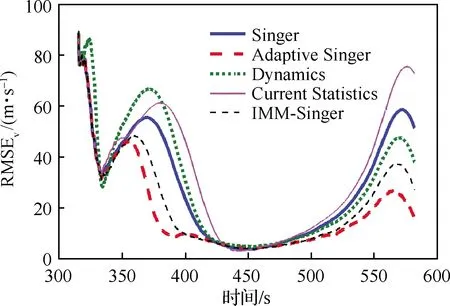
圖17 速度RMSE(軌跡2)Fig.17 RMSE of velocity (trajectory 2)

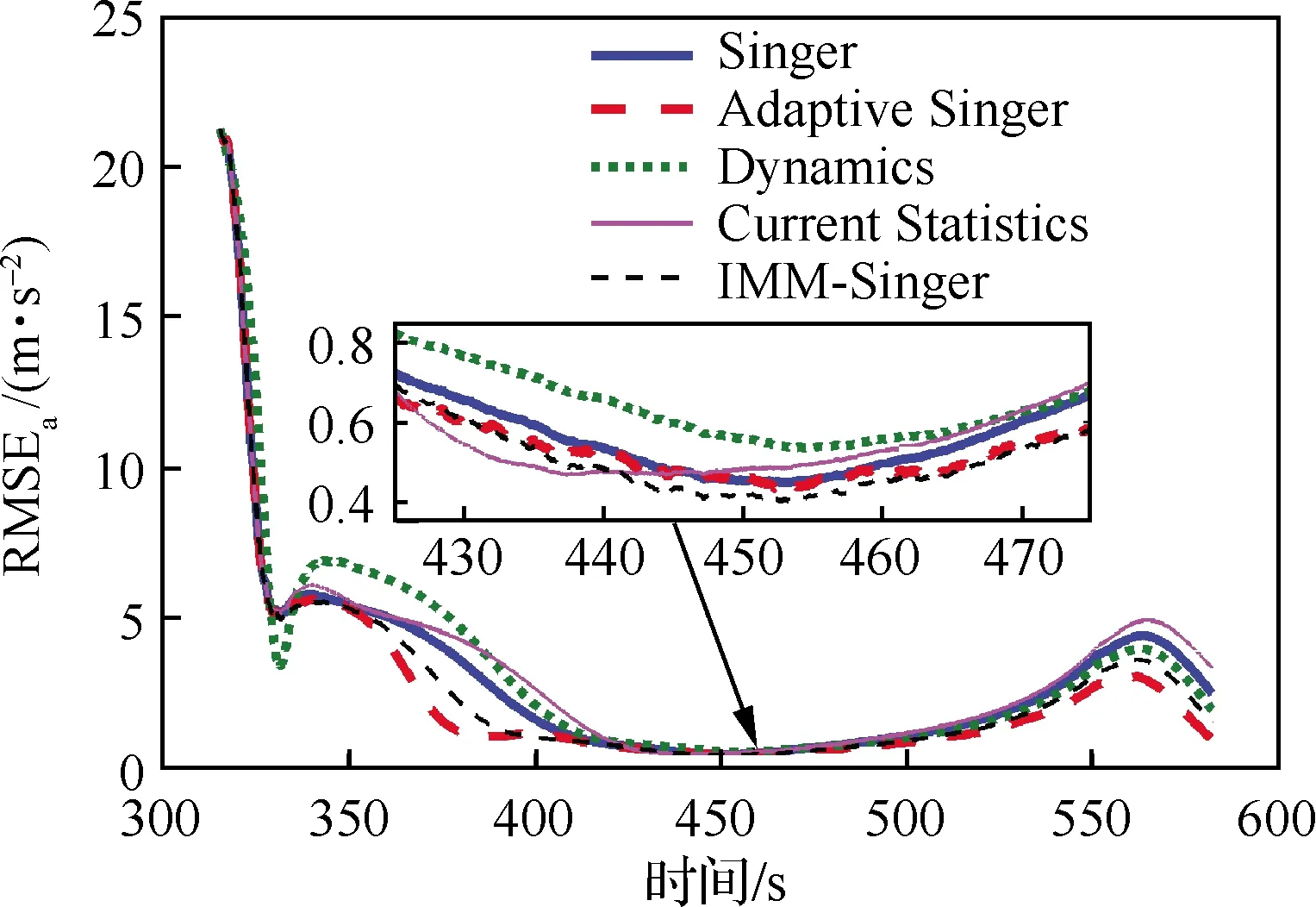
圖18 氣動力加速度RMSE(軌跡2)Fig.18 RMSE of aerodynamic acceleration (trajectory 2)

通過對不同軌跡的跟蹤濾波表明，所設計的“Adaptive Singer”對HGT的階躍機動和連續(xù)幅值變化的機動均具有較好的適應性。圖19給出了各方法單次跟蹤濾波的計算時間，可看出“IMM-Singer”約為其他方法的2倍，計算量大。相比于其他幾種方法，“Adaptive Singer”不僅濾波精度高，而且計算量幾乎沒有增加，實時性好。

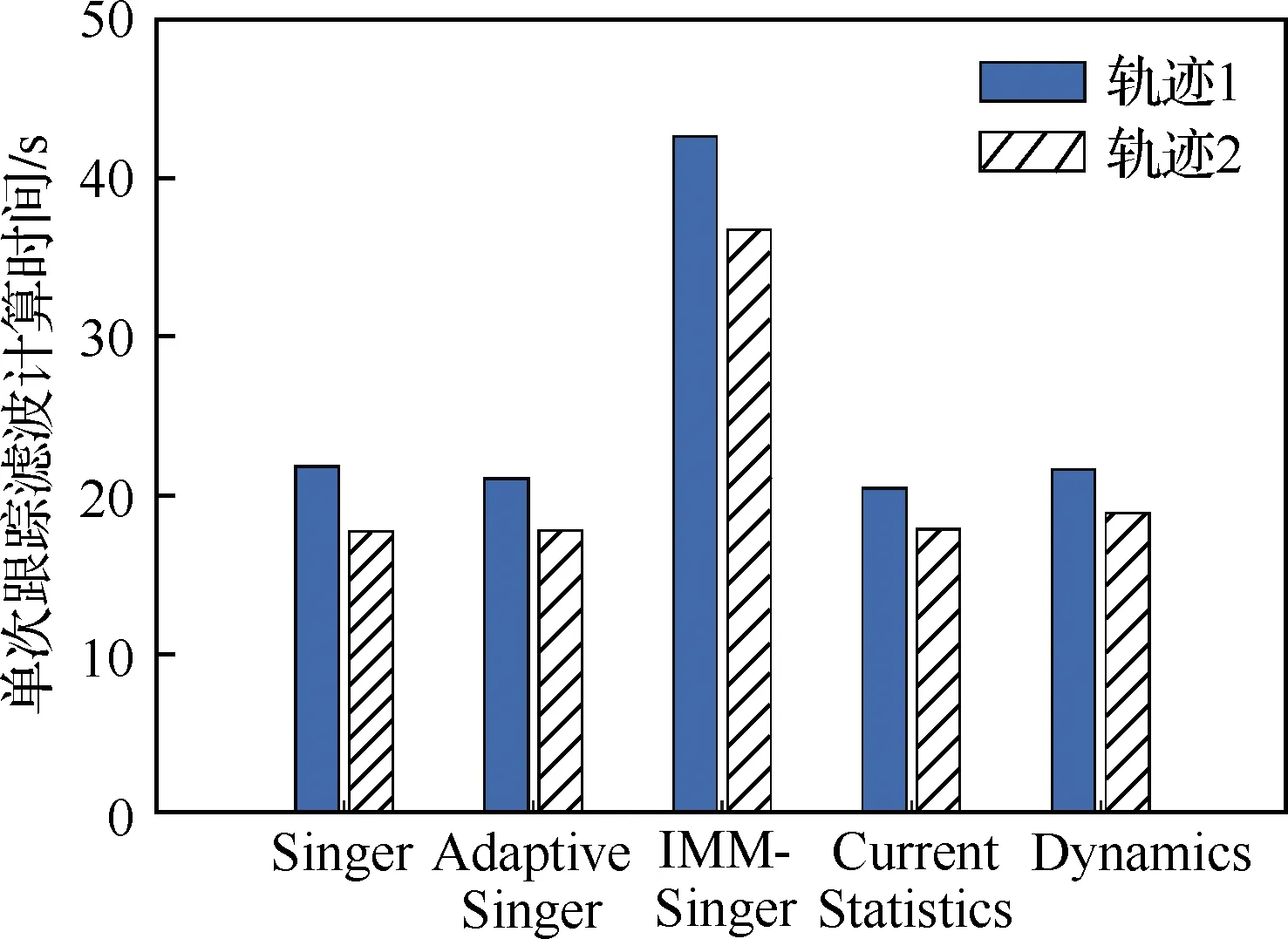
圖19 單次跟蹤濾波計算時間Fig.19 Computational time for single tracking filtering

4 結 論

為了精確跟蹤機動模式多樣的高超聲速滑翔目標，基于正交性原理和UKF算法提出了一種機動頻率自適應的跟蹤方法。通過仿真驗證，得到如下3點結論：

1) 由于HGT機動形式多樣，幾乎無法用固定的跟蹤模型將其囊括，因此狀態(tài)模型誤差固然會存在。

2) 介于CV和CA模型之間的Singer模型可作為表征HGT機動的基礎模型，再結合其他方法合理地調整其機動頻率，降低模型誤差。

3) 所提的“Adaptive Singer”方法能夠較好地適應HGT的多種機動形式，與利用交互式多模型進行機動頻率自適應的方法相比，跟蹤精度高，計算量小。

(A1)

式中:F1=vx，F(xiàn)2=vy，F(xiàn)3=vz，F(xiàn)4、F5和F6的表達式分別為

(A2)

Rosinμo)sin2Bo-(pz+Rocosμo)·

sinBocosBo]-2ωvxsinBo+ay

(A3)

Rocosμo)cos2Bo-(py-Rosinμo)·

sinBocosBo]+2ωvxcosBo+az

(A4)

F7、F8和F9的表達式為

(A5)

附錄B

若從動力學角度對HGT氣動加速度進行建模，由于其采用傾側轉彎控制方式，則氣動力加速度的形式為[1]

(B1)

式中：ρ為大氣密度，近似為高度的指數函數;v為相對速度v的模;CVtoR為目標速度坐標系至雷達坐標系的轉換矩陣;η為目標的面質比。將式(B1)中的右邊部分分為可用目標位置和速度表示的量和不可表示的量，具體形式為[7,24]

(B2)

式中：M的表達式為

(B3)

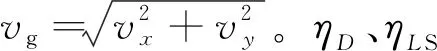
(B4)

式中：γ為雷達坐標系至目標速度坐標系轉換過程中的滾轉角。通常情況下，HGV的面質比、氣動系數和制導控制規(guī)律等先驗信息均難以獲知，因此廣義氣動系數是待估計的未知量。由于HGT在飛行過程中受到熱流密度、動壓、過載和控制量等因素的制約，其控制變量—攻角和傾側角的變化應相對平緩，可用維納隨機過程來表征廣義氣動系數的變化，形式為[6]

(B5)

式中：wD、wLS和wLC為互不相關的零均值高斯白噪聲。將式(11)中ax、ay和az分別替換為ηD、ηLS和ηLC即為動力學模型的狀態(tài)向量，其狀態(tài)方程的形式與式(10)一致。