基于神經(jīng)網(wǎng)絡(luò)的導(dǎo)彈氣動參數(shù)預(yù)測

原智杰，張公平，崔 茅，唐 煒*

(1.西北工業(yè)大學(xué) 自動化學(xué)院，西安 710129；2.中國空空導(dǎo)彈研究院，河南 洛陽 471009；3.航空制導(dǎo)武器航空科技重點實驗室，河南 洛陽 471009)

0 引 言

導(dǎo)彈結(jié)構(gòu)的優(yōu)化是指根據(jù)導(dǎo)彈的氣動性能以及設(shè)定的預(yù)期目標設(shè)計導(dǎo)彈的氣動布局，即對導(dǎo)彈的幾何外形參數(shù)進行調(diào)整，確定導(dǎo)彈機械結(jié)構(gòu)中各個氣動部件(彈頭、彈身、彈翼和舵面等)的形狀、尺寸以及安裝位置的工作過程[1]。導(dǎo)彈氣動性能的優(yōu)良則反映出導(dǎo)彈的氣動布局是否合理，是否需要進一步優(yōu)化，而導(dǎo)彈飛行時的各種氣動參數(shù)能直接反映出導(dǎo)彈的氣動性能。傳統(tǒng)的直接獲取導(dǎo)彈氣動參數(shù)的方法主要有三種[2]：理論計算法、風(fēng)洞試驗法、飛行試驗法。理論計算法過程復(fù)雜，風(fēng)洞試驗法和飛行試驗法存在過程費用極其昂貴、測試周期長等缺點[3-8]。

人工神經(jīng)網(wǎng)絡(luò)技術(shù)被應(yīng)用于模式識別、函數(shù)擬合、聚類問題等，飛行器氣動參數(shù)辨識也成為其應(yīng)用的一個領(lǐng)域。1993年，Linse D J和Youssef H M等人相繼將神經(jīng)網(wǎng)絡(luò)理論與氣動力參數(shù)的辨識問題相結(jié)合，應(yīng)用于氣動參數(shù)的估計[9-10]。2000年，Richardson K A建立了基于徑向基函數(shù)的氣動參數(shù)模型[11]。2011年，美國奧本大學(xué)教授Carpenter M等人提出了一種利用單隱含層神經(jīng)網(wǎng)絡(luò)進行導(dǎo)彈氣動參數(shù)預(yù)測的方法[12]。2016年，Carpenter M等人又提出了一種利用神經(jīng)網(wǎng)絡(luò)與雷達遙測系統(tǒng)相結(jié)合的快速識別導(dǎo)彈類型的方案[13]。張瑞民等人基于BP神經(jīng)網(wǎng)絡(luò)建立了飛機在大攻角狀態(tài)下的氣動模型[14]。史志偉等人討論了基于徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)的非線性非定常氣動模型[15]。王博斌等人基于RBF神經(jīng)網(wǎng)絡(luò)模型展開研究，對翼面不同振幅下的頻域氣動特性進行預(yù)測[16]。朱莉等人采用BP神經(jīng)網(wǎng)絡(luò)對翼型進行氣動力建模，提出了一種翼型優(yōu)化設(shè)計方法[17]。

傳統(tǒng)的工程擬合法氣動建模是根據(jù)氣動力的物理特性、統(tǒng)計規(guī)律等，利用數(shù)學(xué)方法獲得氣動力與飛行狀態(tài)、氣動外形等參數(shù)之間的數(shù)學(xué)關(guān)系式，其適用于狀態(tài)范圍變化較小的局部氣動建模。對于狀態(tài)參數(shù)變化范圍較大，且氣動外形復(fù)雜的飛行器，氣動力與狀態(tài)參數(shù)以及其他參數(shù)間的關(guān)系呈現(xiàn)高度非線性，傳統(tǒng)的數(shù)學(xué)建模方法很難給出準確描述；而神經(jīng)網(wǎng)絡(luò)氣動建模過程不需要考慮輸入輸出之間非線性程度，通過大量氣動力數(shù)據(jù)的機器學(xué)習(xí)，建立氣動模型，具有良好的學(xué)習(xí)能力及非線性擬合能力，是處理非線性函數(shù)逼近的有效方法。

本文利用導(dǎo)彈DATCOM軟件計算已知外形幾何參數(shù)的導(dǎo)彈在設(shè)定的飛行條件下對應(yīng)的氣動系數(shù)，將幾何參數(shù)、飛行條件參數(shù)及氣動系數(shù)作為研究數(shù)據(jù)，基于BP神經(jīng)網(wǎng)絡(luò)建立氣動模型，并驗證利用該模型進行氣動參數(shù)預(yù)測的可行性。用神經(jīng)網(wǎng)絡(luò)氣動模型獲取氣動參數(shù)的方法較傳統(tǒng)方法節(jié)省了風(fēng)洞試驗和飛行試驗昂貴的試驗費用與時間成本，這在導(dǎo)彈研發(fā)過程中有著極為重要的意義。

1 神經(jīng)網(wǎng)絡(luò)建模

1.1 氣動模型的形式

氣動模型是表征飛行器氣動力/力矩與飛行狀態(tài)、氣動外形等參數(shù)之間關(guān)系的函數(shù)。通常可以表示為

Ci=f(H,Ma,α，β，ωx,ωy,ωz,δe,δr,δa，…)

(1)

式中：H，Ma，α，β分別為高度、馬赫數(shù)、攻角、側(cè)滑角；ωx，ωy，ωz分別為滾轉(zhuǎn)、偏航和俯仰角速度;δe,δr,δa分別為升降舵、方向舵和副翼舵偏角。本文以Ci(i=N，M，A，Y，L，D)表示的氣動力/力矩系數(shù)，反映導(dǎo)彈的氣動特性。

1.2 BP神經(jīng)網(wǎng)絡(luò)

BP神經(jīng)網(wǎng)絡(luò)(Back Propagation Neural Network)是一種基于誤差反向傳播的神經(jīng)網(wǎng)絡(luò)，其算法的核心部分是BP算法，由輸入信號的前向傳播和誤差的反向傳播組成了BP神經(jīng)網(wǎng)絡(luò)的整個學(xué)習(xí)過程。根據(jù)反向傳播的誤差信號對神經(jīng)網(wǎng)絡(luò)的閾值和權(quán)值進行調(diào)整，神經(jīng)網(wǎng)絡(luò)訓(xùn)練結(jié)束的標志，是誤差信號達到設(shè)定的訓(xùn)練目標或者迭代次數(shù)達到設(shè)定值。BP神經(jīng)網(wǎng)絡(luò)雖然具有能夠逼近任意非線性函數(shù)的優(yōu)勢，但也有一些缺陷制約其發(fā)展：收斂速度慢、易陷入局部最小、網(wǎng)絡(luò)的一些參數(shù)確定方法不定等[18]。

1.3 思維進化算法

思維進化算法(Mind Evolutionary Algorithm)是一種將計算機科學(xué)和生物進化結(jié)合的一種隨機搜索算法，其基本思路為初始種群按照一定規(guī)則生成，并從中選擇出更適應(yīng)環(huán)境的個體組成優(yōu)勝群體；由選擇出的優(yōu)勝群體進行個體的生成，產(chǎn)生更多的子群體；在生成的子群體內(nèi)部執(zhí)行操作過程中的趨同操作，直到子群體中的個體發(fā)展至成熟階段，同時記錄此時各群體具體的得分信息；在執(zhí)行趨同操作后，子群體中的個體均發(fā)展成熟，記錄的具體得分信息被不斷公布在公告板上，通過得分信息的對比，得到最優(yōu)的群體即得到問題的最優(yōu)解[19]。

1.4 建模思路

利用思維進化算法對BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值進行優(yōu)化。首先，根據(jù)BP神經(jīng)網(wǎng)絡(luò)的拓撲結(jié)構(gòu)，將解空間映射到編碼空間，每個編碼對應(yīng)問題的一個解(即個體)。根據(jù)BP神經(jīng)網(wǎng)絡(luò)拓撲結(jié)構(gòu)確定編碼長度。然后，選取訓(xùn)練集的均方誤差的倒數(shù)作為各個個體與種群的得分函數(shù)，利用思維進化算法，經(jīng)過不斷迭代，輸出最優(yōu)個體，并以此作為初始權(quán)值和閾值，訓(xùn)練BP神經(jīng)網(wǎng)絡(luò)。

根據(jù)上述設(shè)計思路，設(shè)計步驟如圖1所示。

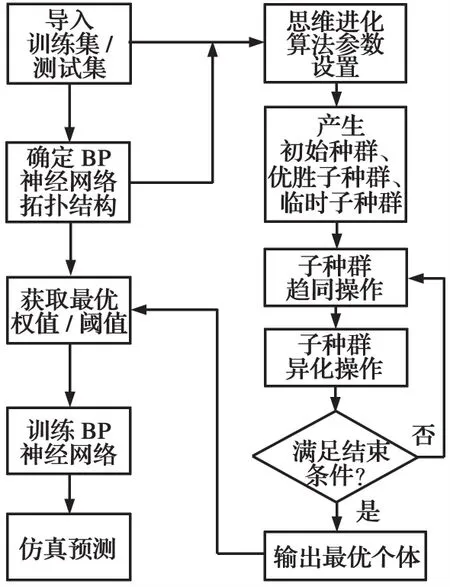
圖1 設(shè)計步驟流程圖Fig.1 Flow chart of design steps

(1) 訓(xùn)練集/測試集導(dǎo)入

將神經(jīng)網(wǎng)絡(luò)的訓(xùn)練數(shù)據(jù)及驗證數(shù)據(jù)導(dǎo)入工作空間。

(2) 初始種群產(chǎn)生

利用編寫好的初始種群產(chǎn)生函數(shù)以及子種群產(chǎn)生函數(shù)生成進化所需種群。

(3) 子種群趨同操作

利用第(2)步中產(chǎn)生的各個種群進行趨同操作，趨同操作結(jié)束與否由種群成熟判別函數(shù)判斷。

(4) 子種群異化操作

趨同操作完成后進行種群的異化操作。

(5) 解析最優(yōu)個體

算法進化過程結(jié)束后，根據(jù)編碼規(guī)則解析出最優(yōu)個體所對應(yīng)的BP神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值。

(6) 訓(xùn)練BP神經(jīng)網(wǎng)絡(luò)

將算法優(yōu)化得到的權(quán)值和閾值設(shè)定為BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值，利用樣本數(shù)據(jù)對神經(jīng)網(wǎng)絡(luò)進行訓(xùn)練。

(7) 仿真預(yù)測、結(jié)果分析

利用訓(xùn)練好的神經(jīng)網(wǎng)絡(luò)進行參數(shù)預(yù)測。

2 算例與分析

2.1 樣本數(shù)據(jù)生成

導(dǎo)彈DATCOM軟件由美國空軍研究室開發(fā)研究。該軟件在已知飛行器幾何外形和飛行條件的前提下，能計算導(dǎo)彈縱向和橫向空氣動力系數(shù)及導(dǎo)數(shù)，具有良好精度。程序采用計算彈箭氣動特性中常用的工程計算方法——部件組合法，該計算方法的核心是由理論分析和實驗驗證得到大量的經(jīng)驗公式。由于充分利用了大量實驗數(shù)據(jù)，該方法能夠保證較高精度，滿足方案設(shè)計階段對氣動力計算的要求。

本研究所用的樣本數(shù)據(jù)以及驗證數(shù)據(jù)均由導(dǎo)彈DATCOM軟件計算生成。導(dǎo)彈外形為面對稱外形，如圖2所示。

圖2 導(dǎo)彈幾何結(jié)構(gòu)模型圖Fig.2 Model diagram of missile’s geometric structure

對導(dǎo)彈彈體幾何參數(shù)、彈翼幾何參數(shù)以及導(dǎo)彈的飛行條件進行設(shè)置后，即可計算出特定彈型在所設(shè)定的飛行條件下的各個氣動系數(shù)。在此，根據(jù)導(dǎo)彈DATCOM軟件中輸入?yún)?shù)間的獨立性，選取彈頭直徑、彈頭長度、彈體直徑、彈體長度、彈體中部彈翼弦長、攻角6個相互獨立的參數(shù)作為神經(jīng)網(wǎng)絡(luò)模型的輸入變量。對于輸出參數(shù)的選擇，則選取氣動性能分析中常用的氣動系數(shù)，選取法向力系數(shù)、俯仰力矩系數(shù)、軸向力系數(shù)、側(cè)力系數(shù)、升力系數(shù)及阻力系數(shù)6個氣動力/力矩系數(shù)作為神經(jīng)網(wǎng)絡(luò)模型的輸出變量。通過編寫MATLAB程序調(diào)用導(dǎo)彈DATCOM軟件，利用程序循環(huán)結(jié)構(gòu)不斷改變6個輸入?yún)?shù)的值，計算得到導(dǎo)彈不同氣動外形對應(yīng)的氣動參數(shù)，并將輸入?yún)?shù)及計算所得的氣動參數(shù)保存為數(shù)據(jù)文件，以此方法獲取16 562組不同的外形參數(shù)及攻角值條件下對應(yīng)的氣動參數(shù)，將這些數(shù)據(jù)用于神經(jīng)網(wǎng)絡(luò)的訓(xùn)練及神經(jīng)網(wǎng)絡(luò)模型的性能驗證。本文所要建立的氣動模型正是6個輸入?yún)?shù)(導(dǎo)彈的幾何參數(shù)和飛行條件參數(shù))與6個輸出參數(shù)(導(dǎo)彈飛行時的氣動參數(shù))間的復(fù)雜非線性函數(shù)關(guān)系。

2.2 神經(jīng)網(wǎng)絡(luò)模型參數(shù)設(shè)置

根據(jù)1.4節(jié)的建模思路建立神經(jīng)網(wǎng)絡(luò)模型，在模型建立過程中需要對一系列參數(shù)進行設(shè)置，主要包括設(shè)置BP神經(jīng)網(wǎng)絡(luò)模型的參數(shù)和思維進化算法的參數(shù)。

本文以包含單個隱含層的BP神經(jīng)網(wǎng)絡(luò)為研究對象，BP神經(jīng)網(wǎng)絡(luò)的拓撲結(jié)構(gòu)由輸入數(shù)據(jù)與輸出數(shù)據(jù)的維數(shù)決定，由2.1節(jié)中所獲取的數(shù)據(jù)知道神經(jīng)網(wǎng)絡(luò)的輸入層節(jié)點數(shù)為6，輸出層節(jié)點數(shù)為6，隱含層的節(jié)點數(shù)由經(jīng)驗公式M=2n+1(M為隱含層節(jié)點數(shù)，n為輸入層節(jié)點數(shù))確定，因此隱含層節(jié)點數(shù)為13。所以，最終確定BP神經(jīng)網(wǎng)絡(luò)的拓撲結(jié)構(gòu)為6-13-6。表1為BP神經(jīng)網(wǎng)絡(luò)參數(shù)設(shè)置。

表1 BP神經(jīng)網(wǎng)絡(luò)參數(shù)Table 1 BP neural network parameters

思維進化算法中需要將個體特征進行編碼，在此選擇個體編碼方法為實數(shù)編碼法，即將每個個體的特征均編碼為一個實數(shù)串，該實數(shù)串包含神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)中各層神經(jīng)元的閾值以及各層之間的連接權(quán)值。當神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)確定之后，可以將思維進化算法進化選擇出的最優(yōu)初始權(quán)值、初始閾值賦值給神經(jīng)網(wǎng)絡(luò)中的對應(yīng)參數(shù)，從而得到一個確定的BP神經(jīng)網(wǎng)絡(luò)。本研究中，由BP神經(jīng)網(wǎng)絡(luò)的拓撲結(jié)構(gòu)6-13-6可計算出個體編碼長度為S=6×13+13+13×6+6=175。表2為思維進化算法參數(shù)設(shè)置。

表2 思維進化算法參數(shù)Table 2 Mind evolutionary algorithm parameters

2.3 建模結(jié)果

將2.1節(jié)中所獲取的16 562組數(shù)據(jù)作為建模樣本輸入，建立氣動模型。同時，將神經(jīng)網(wǎng)絡(luò)模型的氣動參數(shù)預(yù)測輸出與原始氣動參數(shù)進行對比。為了更為明顯地說明模型的預(yù)測結(jié)果，又用導(dǎo)彈DATCOM軟件模擬計算出某特定尺寸的彈型在不同攻角條件的氣動參數(shù)，用于驗證模型的預(yù)測能力。

2.3.1 樣本擬合結(jié)果

將神經(jīng)網(wǎng)絡(luò)氣動模型對樣本數(shù)據(jù)的氣動參數(shù)預(yù)測結(jié)果與原始氣動參數(shù)進行對比，對比結(jié)果如圖3所示。

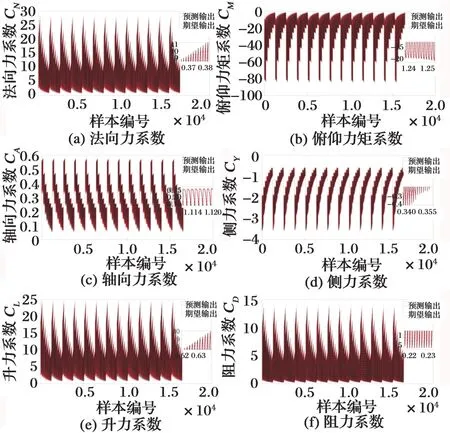
圖3 氣動力和力矩系數(shù)預(yù)測結(jié)果Fig.3 Prediction results of aerodynamic and moment coefficients

表3為神經(jīng)網(wǎng)絡(luò)模型對樣本數(shù)據(jù)中氣動參數(shù)的預(yù)測精度情況。

由圖3樣本擬合結(jié)果可見，6個氣動參數(shù)的預(yù)測輸出曲線與期望輸出曲線的一致性比較好。由表3可見，6個氣動參數(shù)預(yù)測值中最大平均誤差為0.702 4，最大均方差為0.876 9，最大誤差百分比為5.55%，說明建立的神經(jīng)網(wǎng)絡(luò)氣動模型能夠較好地擬合氣動參數(shù)。

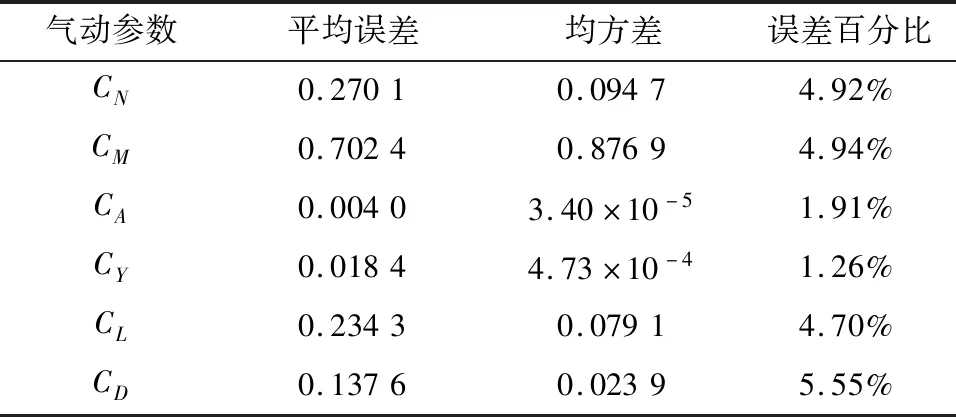
表3 樣本參數(shù)預(yù)測精度Table 3 Sample parameter prediction accuracy

2.3.2 單個彈型擬合結(jié)果

將單個彈型的幾何參數(shù)及攻角作為神經(jīng)網(wǎng)絡(luò)模型的輸入?yún)?shù)，神經(jīng)網(wǎng)絡(luò)氣動模型的氣動參數(shù)預(yù)測輸出與期望輸出(氣動參數(shù)原始值)對比結(jié)果如圖4所示。

表4為神經(jīng)網(wǎng)絡(luò)模型對單個彈型的氣動參數(shù)預(yù)測精度情況。

由圖4中單個彈型的氣動參數(shù)預(yù)測結(jié)果可見，6個氣動參數(shù)預(yù)測輸出曲線與期望輸出曲線一致性較好，同時明顯可見各個氣動參數(shù)隨攻角變化的趨勢，符合氣動特性規(guī)律。由表4可見，6個氣動參數(shù)預(yù)測值中最大平均誤差為0.455 1，最大均方差為0.281 0，最大誤差百分比為6.87%，預(yù)測精度較好，利用該模型可以對氣動參數(shù)進行預(yù)測，用于導(dǎo)彈設(shè)計初始階段的氣動特性分析。

3 結(jié) 論

利用導(dǎo)彈DATCOM軟件計算已知幾何參數(shù)的導(dǎo)彈在設(shè)定飛行條件下的氣動參數(shù)作為訓(xùn)練樣本，通過對所選取的6個輸入?yún)?shù)(幾何參數(shù)和飛行條件參數(shù))及6個輸出參數(shù)(氣動參數(shù))進行氣動力建模，得到了對應(yīng)的神經(jīng)網(wǎng)絡(luò)氣動力模型，并對模型的預(yù)測精度進行說明。通過建模及分析，得到如下結(jié)論：

(1) 利用神經(jīng)網(wǎng)絡(luò)建立的氣動模型對導(dǎo)彈氣動外形與氣動參數(shù)間的復(fù)雜非線性關(guān)系具有很好的擬合效果，預(yù)測結(jié)果的平均誤差、誤差百分比和均方誤差均比較小。

(2) 利用思維進化算法優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)建立的氣動模型，滿足導(dǎo)彈氣動外形與氣動參數(shù)間復(fù)雜非線性擬合要求，為導(dǎo)彈氣動參數(shù)的獲取開辟了新的思路，同時也為導(dǎo)彈設(shè)計初始階段氣動特性的分析提供了新的技術(shù)途徑。

(3) 該氣動建模方法可快速融合已有的飛行試驗數(shù)據(jù)、風(fēng)洞試驗數(shù)據(jù)，利用導(dǎo)彈DATCOM計算所得數(shù)據(jù)結(jié)果建立神經(jīng)網(wǎng)絡(luò)模型，對新的氣動外形對應(yīng)的氣動參數(shù)進行預(yù)測，可有效節(jié)省風(fēng)洞試驗和飛行試驗的費用。在未來的研究中將增大訓(xùn)練數(shù)據(jù)的數(shù)量，利用導(dǎo)彈DATCOM計算時擴大輸入?yún)?shù)類別及其變化范圍，以擴大模型的預(yù)測范圍，直接利用其對所設(shè)計彈型的氣動參數(shù)進行預(yù)測。