無人直升機吊掛系統滑模反步減擺控制

何榮榮，陳 謀，吳慶憲，劉 楠

(南京航空航天大學 自動化學院，南京 210016)

0 引 言

直升機機外吊掛運輸一直是軍用和民用直升機的重要任務之一，地面設備無法取代其在軍事和民用救援領域的作用，而且直升機是在需要垂直起降和懸停能力的作戰中最合適的選擇[1]。然而,直升機吊掛系統復雜的非線性和動態不穩定性使其難以控制，并且在運輸過程中，吊掛負載的振蕩是極其危險的，當負載的振蕩幅度超過限度時，可能對負載產生損壞甚至威脅到無人直升機的安全[2]。所以直升機吊掛飛行安全問題是目前亟需解決的問題，控制直升機吊掛系統，減小吊掛負載振蕩對提高飛行安全十分重要。

目前，國內外對于直升機吊掛的研究主要是對直升機吊掛飛行的空氣動力學模型的建立和飛行穩定性的研究和理論分析，無人直升機吊掛系統飛行過程中吊掛負載有效減擺的方法還需進一步研究。文獻[2-3]對直升機吊掛系統的穩定性進行分析，并設計了線性縱向模型反步控制器。文獻[4]基于CFD方法對CONEX吊掛物進行氣動建模，針對直升機吊掛耦合系統操穩特性進行了相關研究，并將模型線性化后設計PID控制器。文獻[5]從氣動導數和運動模態兩個層面分析了直升機吊掛飛行中的耦合。文獻[6]建立了直升機吊掛耦合非線性模型，并在小擾動線性化后進行吊掛飛行操縱響應的時域和頻域特性分析。文獻[7-9]主要對直升機吊掛系統飛行過程中的穩定性和平衡特性進行了分析和研究。盡管無人直升機吊掛系統已有較多的研究成果，但其吊掛子系統全狀態非線性魯棒減擺控制還需進一步研究。

本文將實現無人直升機平面飛行中的有效吊掛減擺控制，受文獻[10]的啟發，建立直升機剛體吊掛的模型，并且采用反步法解算出減擺的虛擬控制律。參考文獻[11]，采用滑模反步和反步的控制方法，對直升機的速度、直升機的姿態角和姿態角速度進行跟蹤控制，最終達到無人直升機吊掛非線性系統的減擺跟蹤控制效果。

1 無人直升機吊掛動力學模型

本文研究的無人直升機吊掛系統由吊索、吊掛負載等組成，圖1所示為其系統組成示意圖[12]。其中；oxyz為機體坐標系，其坐標原點o在直升機重心的正下方；ox軸以直升機參考平面內平行機身軸線并指向直升機前方為正；oy軸以垂直直升機參考面并指向直升機右方為正；oz軸以參考面內垂直xoy平面并指向直升機下方為正；θL，φL分別為直升機吊掛負載的側擺角和后擺角。

圖1 直升機吊掛系統示意圖Fig.1 Schematic diagram of helicopter slung-load system

1.1 直升機動力學模型的建立

本文建立的六自由度無人直升機非線性系統模型處于懸停和低速平飛狀態，首先假設[13]：(1)地面坐標系為慣性坐標系；(2)直升機是質量分布不變的剛體，質心不發生變化；(3)直升機嚴格左右對稱；(4)忽略槳葉彈性形變，且主旋翼轉速不變。

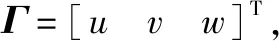
(1)

(2)

式中：

R11=cosθcosφ

R12=sinφsinθcosφ-cosφsinφ

R13=cosφsinθcosφ+sinφsinφ

R21=cosθsinφ

R22=sinφsinθsinφ+cosφcosφ

R23=cosφsinθsinφ-sinφcosφ

R31=-sinθ

R32=sinφcosθ

R33=cosφcosθ

(3)

H為姿態角到姿態角速度的轉換矩陣，具體表達式如下[13]：

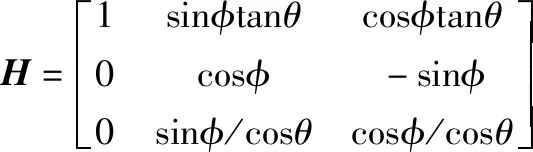
(4)

1.2 吊掛子系統模型的建立

本文建立的吊掛非線性動力學系統模型為剛體模型，為建立此模型，做以下假設[14]：

(1) 吊索為剛體，無重力和空氣阻力；

(2) 吊索時刻處于緊繃的狀態；

(3) 吊掛點處于直升機的重心的正下方；

(4) 吊掛負載處于較小角度振蕩。

吊掛子系統的輸出包括吊掛負載的后擺角φL和側擺角θL，負載相對于吊掛點在圖1所示坐標PL為[15]

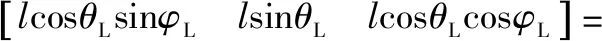
(5)

式中：l為吊索的長度。吊掛負載相對于直升機重心的坐標P為[15]

P=PL+PH

(6)

式中：

(7)

其中：lH為吊掛點到直升機質心的直線距離；PH為吊掛點在以直升機重心為原點的機體坐標系的坐標。吊掛負載的絕對速度為[15]

(8)

負載作用在直升機上的力F與力矩Mb可表示為[15]

(9)

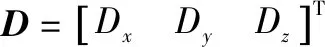
(10)

通過解算式(10)可得出吊掛負載的動力學方程，然后通過反步法解算出為達到減擺效果所需的直升機速度，最后控制直升機的速度即可達到減擺效果。

2 無人直升機吊掛系統減擺控制

無人直升機吊掛的減擺控制原理如圖2所示[15]。

由圖2可知，直升機剛體吊掛系統滑模減擺控制的原理如下：首先，通過反步法得到控制吊掛物擺角穩定的直升機速度；然后，設計滑模反步和反步控制器對直升機速度及姿態進行跟蹤控制[16]，最終達到減擺效果。

2.1 吊掛擺角減振虛擬控制律解算

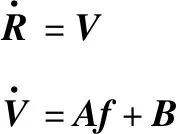
(11)

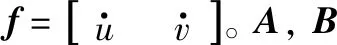
(12)

式中：

(13)

定義變量R，V為

(14)

擺角和擺角速度的跟蹤誤差可定義為

e1=Rd-R

e2=Vd-V

(15)

式中：Rd，Vd為擺角和擺角速度的期望輸入。設計吊掛子系統反步法虛擬控制律為

(16)

結合式(14)～(16)，對e1求導可得：

(17)

設計減擺虛擬控制律為

(18)

式中：k1，k2為設計的正定矩陣。由于直升機吊掛負載處于較小角度振蕩，可將矩陣A簡化為以下形式：

(19)

根據吊掛子系統模型建立假設條件4將da簡化，簡化后的表達式為

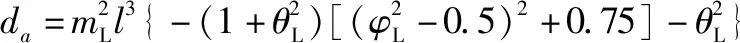
(20)

根據假設條件4可得da不為0，且A為可逆矩陣。選擇李雅普諾夫函數為

(21)

結合式(15)，(17)對式(21)求導可得：

(22)

2.2 直升機速度控制

直升機速度子系統采用反步法，系統共有三個輸入Tmr，φ，θ，分別為主旋翼總矩輸入、滾轉角和俯仰角，三個輸出u，v，w分別為直升機三個方向的線速度，并假設偏航角φ=0，直升機速度子系統可表示為

(23)

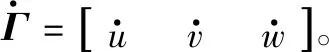
e3=Γ-Γd

(24)

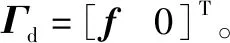
(25)

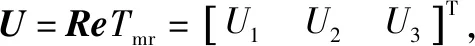
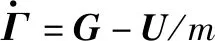
(26)

設計速度子系統控制律為

(27)

式中：k3為設計的正定矩陣，可由直升機子系統模型解算出：

(28)

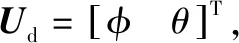
(29)

對式(29)求導得：

(30)

2.3 直升機姿態滑模反步控制

直升機姿態子系統采用滑模反步控制方法[18]。直升機姿態子系統的三個輸入L，M，N分別為直升機所受三個方向的分力矩，三個輸出φ，θ，φ分別為直升機的滾轉角、俯仰角、偏航角。考慮姿態系統的未知干擾，則直升機姿態子系統可表示為

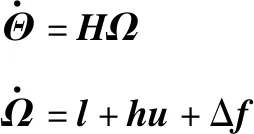
(31)

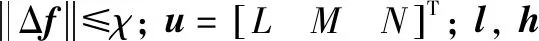
(32)

定義直升機姿態子系統的姿態角和姿態角速率的跟蹤誤差為

e4=Θd-Θ

e5=Ωd-Ω

(33)

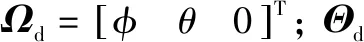
(34)

式中：k4為設計的正定矩陣。對e4求導并將式(34)代入式(33)可得：

(35)

設計滑模面為

s=e4+e5

(36)

對式(36)求導，并將式(35)和式(33)代入可得：

(37)

最終設計姿態控制律為[19]

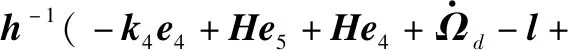
(38)

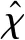
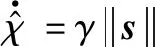
(39)

式中：γ>0為設計的參數。設計李雅普諾夫函數為

(40)

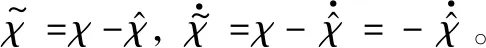
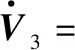
(41)

3 穩定性分析

以上關于直升機剛體吊掛耦合非線性系統減擺控制的穩定性分析可歸納為如下定理：

定理1：本文建立的剛性直升機吊掛非線性系統，對吊掛子系統(11)的減擺虛擬反步控制律按式(18)設計，對直升機速度子系統(23)的反步控制律按式(26)設計且對直升機姿態子系統(31)的滑模反步控制律和自適應律按式(38)～(39)設計，則閉環系統的所有信號收斂。

證明：選擇李雅普諾夫函數為

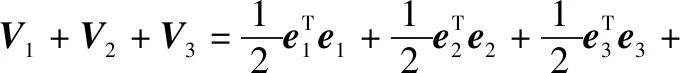
(42)

將式(42)求導，并考慮式(15)，(17),(18)，(34)，(36)可得以下表達式：

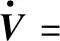
(43)

式中：k5=min{2k1,2k2,2k3,2k4,2η-I}，由李雅普諾夫穩定性分析方法可知，本文所設計的無人直升機吊掛減擺系統是閉環穩定的，證畢。

4 仿真結果

為了驗證直升機吊掛系統控制器設計的有效性，進行數字仿真，仿真參數如表1所示。

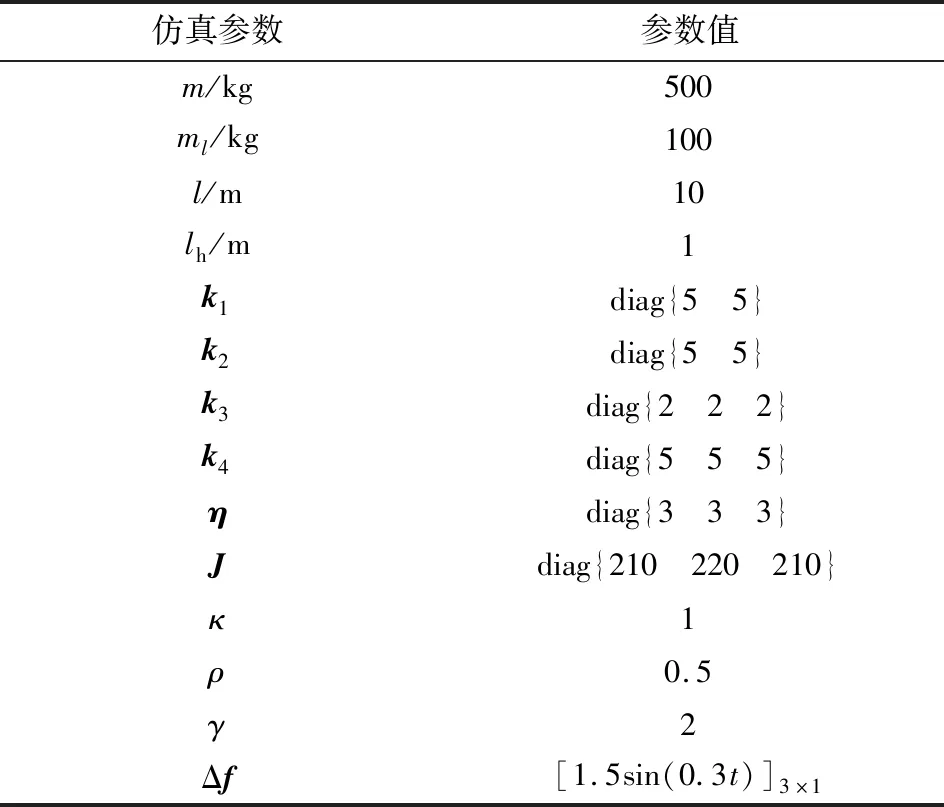
表1 仿真參數Table 1 Simulation parameters

通過Simulink仿真可得如圖3～7所示的仿真結果。

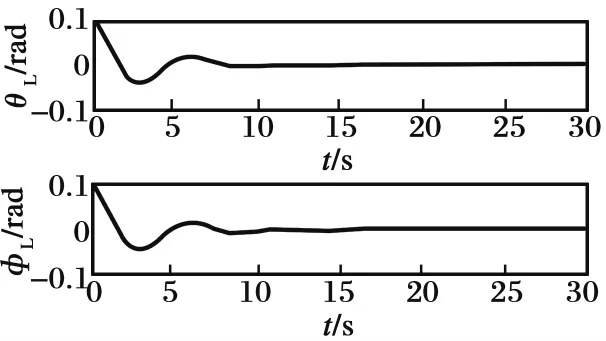
圖3 直升機吊掛減擺控制仿真結果Fig.3 Simulation results of helicopter anti-swing control

吊掛子系統與直升機速度子系統依然使用控制律(17)，(24)，設計直升機姿態子系統傳統反步法虛擬控制律為

(44)

式中：k6為設計的正定矩陣，反步法控制律為

(45)

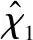
(46)

式中：γ1>0。

直升機姿態子系統反步法控制仿真參數如表2所示。Simulink仿真結果如圖8所示。

表2 仿真參數Table 2 Simulation parameters

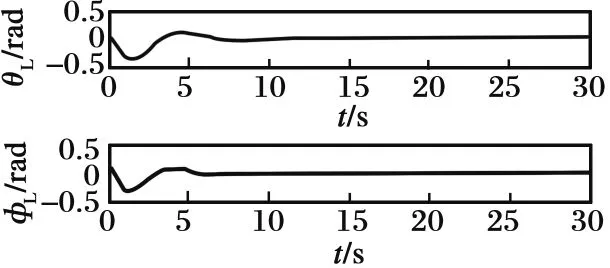
圖8 系統傳統反步控制仿真結果Fig.8 Simulation results of system traditional backstepping control

將系統參數m，Jxx，Jyy,Jzz攝動50 kg，20，15，25,參數攝動后的Simulink仿真結果如圖9所示。

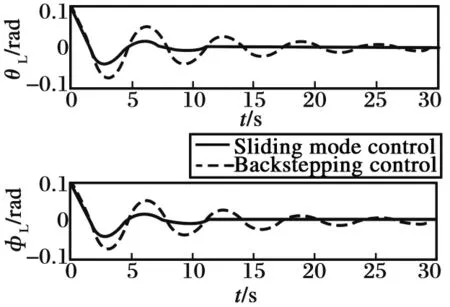
圖9 參數攝動后系統滑模反步控制與傳統反步控制仿真結果對比Fig.9 Comparison of simulation results between sliding mode backstepping control and traditional backstepping control after parameter perturbation

由圖3可知，吊掛負載開始有一較小角度(本文假設初始擺角為0.1 rad)的擺動，通過所提出的一系列滑模反步和反步減擺跟蹤控制，直升機吊掛負載得以減擺，由于直升機飛行速度較低，空氣阻力相對于負載的重量較小，故吊掛負載幾乎垂直于直升機前進，擺角穩定在0°左右。由圖4和圖5可知，直升機最終以初始速度(本文直升機x，y方向初始飛行速度均為5 m/s，z方向初始速度為0 m/s)于98 m的高度平飛，由圖6和圖7可知直升機姿態角速度和姿態角均穩定在0 rad/s和0 rad，最終對直升機速度與姿態以及吊掛子系統的擺角均完成跟蹤控制，進一步證明了本文設計的一系列控制器的有效性。由圖3以及圖8～9可知，與傳統的直升機吊掛系統的反步控制方法相比，本文設計的滑模反步控制方法具有對系統參數不敏感的特性，魯棒性更強，且本文針對非線性系統進行跟蹤減擺控制相對于線性橫縱向解耦系統控制更具有現實意義。

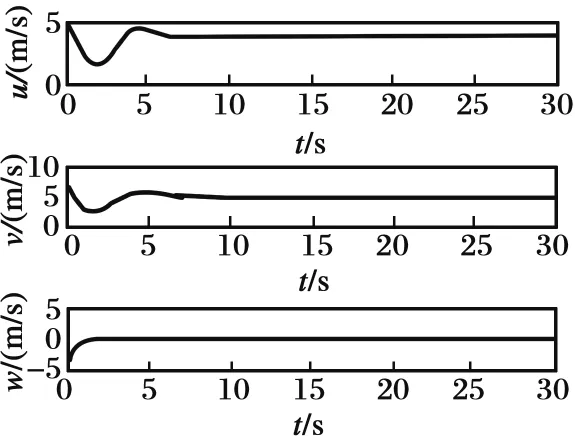
圖4 直升機速度仿真結果Fig.4 Simulation results of helicopter velocity

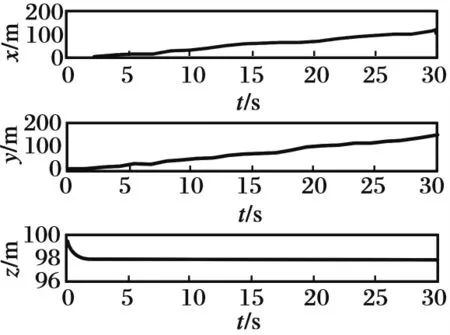
圖5 直升機位移仿真結果Fig.5 Simulation results of helicopter displacement

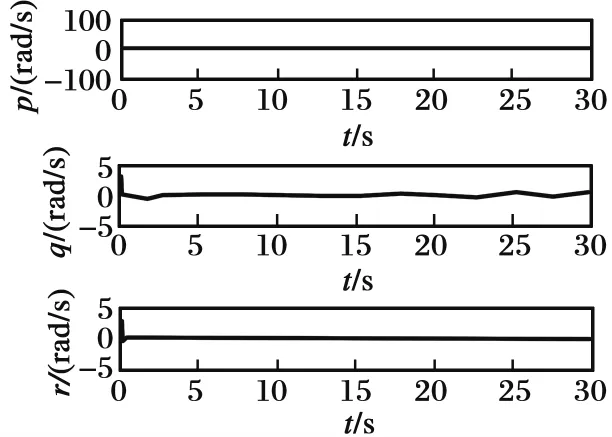
圖6 直升機姿態角速度仿真結果Fig.6 Simulation results of helicopter attitude angular velocity

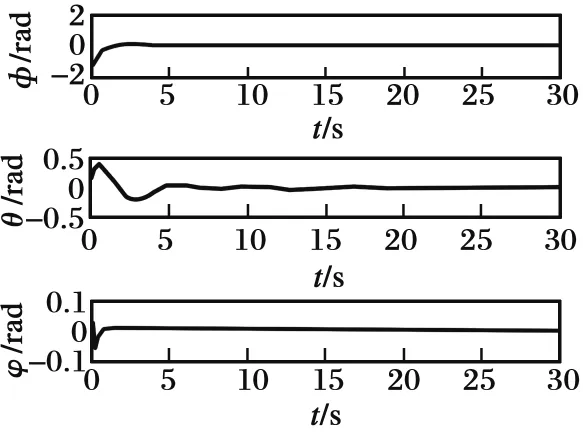
圖7 直升機姿態角仿真圖Fig.7 Simulation results of helicopter attitude angle

5 結 論

本文針對建立的無人直升機剛體吊掛耦合非線性系統，以減小吊掛負載的擺角以及控制直升機速度和姿態為目標，對直升機速度和姿態，以及吊掛負載的擺角均進行了跟蹤控制，并通過Simulink仿真對所設計控制器的有效性進行了驗證。基于已有的理論基礎，在不對直升機吊掛系統進行橫縱向解耦和線性化的情況下，不僅對吊掛負載進行非線性減擺控制，也對直升機平面運動的速度以及姿態進行非線性控制，更具有現實意義，且滑模反步法對系統參數不敏感，閉環系統魯棒性更強。但本文僅考慮直升機平面運動時的擺角控制，僅限小角度擺動，并且將吊掛負載視為質點，沒有考慮其姿態建模，今后將對直升機空間運動的減擺控制展開研究。