基于輕量級深度神經網絡的電磁信號調制識別技術

張思成，林云，涂涯，Shiwen Mao

（1.哈爾濱工程大學信息與通信工程學院，黑龍江 哈爾濱 150001；2.奧本大學電子和計算機工程學院，奧本 36849）

1 引言

移動通信系統由1G、2G 到3G、4G，現已進入5G 的商業發展階段。5G 的商業部署工作已經展開，將提供大規模連接、高可靠性和低時延的服務。本著“商用一代、規劃一代”的發展理念，部分國家已經展開了對6G 的研究與探索。6G 將依賴新的使能技術實現全球覆蓋范圍，更高的頻譜、能源、成本效率，更加安全，更高的數據速率，更低的時延，更高的連接密度，更高的全自動智能性，以獲得更好的服務質量、體驗質量，實現萬物互聯[1]。同時，6G 時代將會是移動通信技術與人工智能技術緊密結合、深度融合的時代，放眼于智能、通信與人類未來三者之間的關系，深入挖掘用戶的需求，實現人?機?物?靈的“萬物互聯”[2]。

伴隨6G 時代的到來，將會產生大量分布式節點，這些分布式節點的智能連接是實現6G 時代萬物互聯的關鍵，而智能連接的基礎是物理層智能信號處理。其中，物理層信號識別將促進自適應調制編碼、聯合信道估計和符號檢測、自適應傳輸功率控制以及更加廣泛的物理層技術的發展[3]。分布式節點實現智能、自動的電磁信號識別將極大地推動6G 萬物互聯的實現。人工智能技術憑借其強大的擬合復雜模型的能力，近幾年得到了迅猛的發展，在各項研究領域中都取得了突破性的進展，其在信號識別與處理問題中已經有豐富的成果。Li 等[4]提出一種基于貝葉斯隨機推斷和最大后驗準則的聯合估計模型，該模型深層表征了調制方案和衰落信道之間的耦合關系，實現識別信號調制方式的同時順序獲取時間相關的衰落狀態。Wang 等[5]使用卷積神經網絡（CNN,convolutional neural network）對信號的眼圖進行識別，可以在寬光信噪比范圍內對4 種調制信號實現100%的識別率。查雄等[6]通過將電磁信號的波形域數據轉化為眼圖與矢量圖形式，獲得信號的淺層次表達，進一步利用多端卷積神經網絡對其進行識別，當信噪比為5 dB 時，識別準確率可達95%。Peng 等[7]將8 種調制信號轉換為星座圖并處理得到灰度圖像和增強灰度圖像，使用CNN 對其進行訓練和測試，仿真結果表明該方法可以有效地對8 種調制信號進行分類。吳佩軍等[8]設計了33層卷積神經網絡ReSENet，采集實測信號作為實驗樣本，使用短時傅里葉變換將信號轉換為時頻圖，實驗結果表明該方法可對多進制相位調制信號實現99.9%的識別準確率。Ji 等[9]針對多徑衰落信道提出盲均衡輔助的深度學習網絡，實驗表明該方法相比不均衡的深度學習方法對正交振幅調制（QAM,quadrature amplitude modulation）類信號的識別精度有顯著提升。Xu 等[10]針對運用CNN 進行調制信號識別的課題展開研究，發現較深的網絡模型不適用于調制信號識別，并使用遷移學習對訓練過程進行了優化，同時使用實測信號進行實驗，識別性能得到了提升。

然而，在追求模型性能提升的同時，模型復雜度與參數量也成倍增長，隨之而來的是過高的計算復雜度與存儲開銷，這對其應用于6G 智能邊緣設備產生了極大的阻礙。桂冠等[11]對人工智能技術應用于物理層無線通信問題中的研究進行了總結與分析，說明了人工智能技術具有諸多優點，模型壓縮與加速技術將是未來無線通信中影響系統帶寬、時延以及安全問題的重要因素。研究者開展了大量工作，研究如何將基于人工智能技術實現的智能信號處理技術部署于資源受限的設備中。Tu 等[12]在文獻[6]的基礎上提出基于點密度的星球圖數據處理方法，使用AlexNet 對其進行識別，準確率有明顯提升，此外，他還根據文獻[13]的方法將模型進行剪枝，在保證準確率的同時，將參數量壓縮至原模型的1.5%～5%，部署在NVIDIA Jetson TX2 上的運行1 000 次的時間為6～8 ms。文獻[14-15]進一步提出激活最大化的評估指標對模型進行評估與剪枝，實驗結果顯示，該方法在不同壓縮率下針對RML2016.a 數據集獲得了同等或更高的識別準確率。陶冠宏等[16]將信號的I/Q 兩路分別提取出來，構建2 行N列的二維圖像，輸入CNN 中進行訓練，測試結果表明該方法可以對8種調制信號實現85%的識別準確率，實際部署后的單信號識別時間為0.1 ms。周鑫等[17]將信號的I/Q 兩路數據經過離散傅里葉變換映射到頻域，經過圖像化處理將多次變換的結果組合為二維頻譜瀑布圖輸入CNN 中進行訓練，實驗結果表明，該方法可以對12 種信號實現86.04%的識別準確率，部署于中等配置的臺式機上的運行時間為33 ms。

以上的研究成果都很難取得準確率與速度上的雙重提升，是因為以往的全精度神經網絡（FNN,full-precision neural network）僅從網絡模型的結構入手進行修剪或稀疏處理，有些方法對模型的容量以及穩健性會有損失；有些方法對計算機運算過程并不友好，在減小模型參數存儲的同時增加了模型的運算時間。考慮計算機本身的數據存儲、訪問、運算以及網絡分類性能，研究人員發現神經網絡在逐層計算過程中，參數的量化空間不需要非常完備也可以對問題模型進行擬合，從而完成正確的分類或檢測，精簡后的網絡參數運算可以用簡單的位操作完成，而不需要復雜的浮點乘法運算，這樣兼顧了保持精度與加速的效果。基于此想法，Dettmers等[18]開發測試了8 bit 浮點的網絡模型，再利用GPU集群測試其性能，在保證模型與預測性能的條件下，速度提升到原來的2 倍。此后出現了各種模型量化的研究，包括16 bit[19]、三值量化[20]與二值量化[21]。目前，主流的模型量化方法分為樸素量化方法和基于優化的量化方法，后者又分為最小量化誤差量化法、改善網絡損失函數量化法和減小梯度誤差量化法[22]。

本文針對6G 中智能邊緣設備的信號識別問題，在已有的電磁信號識別算法研究的基礎上，將電磁信號的I/Q 數據繪制為星座圖，以將電磁信號從波形域具象化為二維圖像，并根據歸一化點密度對其添加顏色信息以實現特征增強；分析現有的信號識別模型的資源開銷，設計并構建了二值化神經網絡（BNN,binary neural network）模型對經過特征增強的圖像域信號進行識別。經過初步實驗證明，所提模型能夠在保證對電磁信號識別準確率的前提下，兼具內存開銷小、數據訪問量低和計算速度高的特點，適合于6G 中資源受限的智能邊緣設備。

2 電磁信號模型

2.1 電磁信號波形域分析

本文實驗選取8 種常用的數字調制信號，分別為4ASK、BPSK、QPSK、OQPSK、8PSK、16QAM、32QAM 和64QAM。信號的基帶波形域為

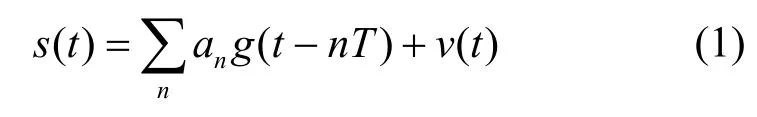
其中，v(t)表示信道環境噪聲，本實驗選擇加性高斯白噪聲；g(t)表示包括成型濾波器、信道濾波器以及匹配濾波器的等效濾波器；an表示發送端符號序列。

對于ASK 類信號，有

其中，Qn=0，In∈{1,2,…,M?1}，M為調制進制數。

對于PSK 類信號，有

對于QAM 類信號，有

2.2 電磁信號的圖像域具象方法

實驗首先通過正交解調獲得電磁信號的I/Q 兩路原始數據，進一步利用I/Q 數據繪制電磁信號的星座圖以將電磁信號具象為二維圖像，并根據歸一化點密度對星座圖上色以實現特征增強。以QPSK為例說明電磁信號圖像域具象方法，如圖1 所示。將I/Q 兩路信號繪制在以同向分量為橫軸，正交分量為縱軸的坐標系中，得到QPSK 信號的星座圖，如圖1 左半部分所示。對QPSK 每一個信號點計算其歸一化點密度，并根據其歸一化點密度的高低對星座圖進行上色以實現特征增強，上色的方法與效果如圖1 右半部分所示。從圖1 中可以看出，經過預處理后的星座圖中每個點不再是獨立以及等信息量的。這種處理方法給星座圖中增加了時間累積的特征，數據特征維度更高，凝聚了更多的調制信號先驗知識，增強其可分性，實現了特征增強的目的。

圖1 電磁信號圖像域具象方法示意

圖2 不同信噪比噪聲下的數據處理效果

計算某一點的歸一化點密度時，以該點為中心繪制的邊長為2r的正方形內，其他信號點的個數與總共接收到信號點的個數的比值為該點的歸一化點密度。第i點的歸一化點密度d(i)為

其中，h(i)表示獲取第i個點的橫坐標值，v(i)表示獲取第i個點的縱坐標值，N表示點的總數，f(x)函數為

由此可得，當信噪比為0 dB、6 dB 以及10 dB的高斯白噪聲時，8 種信號的數據處理效果如圖2所示。

3 二值化深度神經網絡

3.1 二值化深度神經網絡原理

本文研究利用BNN 完成圖像域的電磁信號調制識別問題。BNN 來源于神經網絡低比特量化的思想的極端情況，其思想為神經網絡在逐層計算過程中，參數的量化空間不需要非常完備也可以對問題模型進行擬合，從而完成正確的分類或檢測。而在模型規模方面，原有的32 bit 浮點數據被1 bit 數據代替，可實現參數總占用減小近32 倍的壓縮效果。另外，位寬為1 的參數之間的計算可以使用簡單的位操作來完成，可省去32 bit 浮點型數據乘法的煩瑣計算，實現加速效果。

本實驗采用的神經網絡二值化方法為神經網絡樸素二值化分類中的確定性二值化方法[22]。在確定性二值化方法中，前向推理時，網絡中二值化層的權重與輸入被量化為±1。量化規則為，大于或等于0 的權重或輸入被量化為+1，而小于0 的被量化為?1，如式(7)所示。

其中，w為網絡中原始的全精度參數，wb為經過二值化后得到的二值化參數。代碼實現時可以用取符號函數sign(?)對參數和輸入取得符號，從而實現二值化。sign(?)函數曲線如圖3 所示。

圖3 sign(?)函數曲線

在計算機實際存儲中，置0 bit 代表參數值為?1，置1 bit 代表參數值為?1，其運算的權值真實數值和計算機變量的乘法運算真值如表1 和表2所示。從表1 中可以看出，經過以上量化規則得到的±1 權重乘法運算與計算機1 bit 變量的同或運算等效，這就將FNN 中的32 bit 浮點乘法運算簡化為1 bit 的同或運算，實現對網絡卷積運算中的乘法進行加速的效果。

表1 權值實際運算真實數值

表2 計算機運算真值

在反向傳播求解梯度進行優化過程中，例如隨機梯度下降等優化算法的實現都是通過每次對網絡進行小步微調，逐漸逼近整個網絡的最優解。而BNN 中，二值參數的值只有+1 和?1，這意味著量化值的每一次更新都會使網絡狀態產生很大的改變，增加了對BNN 中參數更新標準的設定。因此，每次訓練時依然需要對原始全精度參數進行優化更新，而在前向推導時進行量化參數操作。

sign(?)函數的梯度在大部分情況下都為0，這將導致二值化參數與原始參數之間的梯度傳播被阻斷。為了避免梯度阻斷問題，將二值化權重的梯度跳過sign(?)函數直接傳播給原始的全精度參數，使二值化參數的梯度作為原始參數的梯度近似，如圖4 所示。Identity 函數的計算式為y=x，其正向傳播相當于不具任何處理的直連函數，而其函數梯度恒等于1，起到了將二值化參數的梯度直接回傳的作用。將Identity 函數與隨機梯度下降等優化算法結合，即可實現原始全精度參數的逐步更新。

3.2 用于電磁信號調制識別的二值化深度神經網絡

本文設計并構建了用于電磁信號調制識別的二值化深度神經網絡模型，在模型整體結構上綜合參考經典的AlexNet 網絡結構[23]，先采用卷積層提取特征，然后采用全連接層對特征分類。

圖4 BNN 訓練極端的前/反向傳播示意

本文分析數據特征設計網絡中每層的類型。從電磁信號的圖像域表現形式可以看出，圖像中每個像素點的量化空間為8 bit 整型，并且其中具有很多明顯的細粒度的信號點的分布特征，但是不存在計算機視覺分類問題中的目標被遮蓋、平移、旋轉等問題，所以在網絡中僅設計第一層為全精度網絡層來提取電磁信號圖像域中的細粒度淺層特征，其參數量化空間為32 bit 浮點型；利用連續的三層二值化網絡層綜合提取不同深度的粗粒度特征。受到本文所選的二值化推理框架DABNN（daquexian’s accelerated binary neural network）未兼容全連接網絡的限制，實驗使用卷積核尺寸為1×1的卷積層替代全連接層[24]。在1×1的卷積層與特征提取部分之間插入過渡層以完成數據尺度的銜接。網絡輸出層得到的結果經過Softmax 層，得到對不同分類的判別概率分布。圖5 為實驗構建的用于電磁信號識別的BNN 結構。

如圖6 所示，除輸出層外，網絡中的層均由三部分構成。Float/Binary Layer 用于特征提取或分類；BatchNormal Layer 用于將數據分布歸一化以加快訓練；MaxPooling Layer 用于實現特征聚合，增強網絡的抗噪聲性能。

圖5 BNN 結構

需要說明的是，在卷積運算的累加運算過程中，因為1 bit 數據無法表達求和運算的結果，所以在累加求和過程中的中間變量仍然需要用更高位數的數據類型。本實驗所設計的BNN 中用到的BatchNormal layer 和MaxPooling Layer 中涉及更精確的運算同樣是二值化參數所無法表達的。綜合考慮各層對中間變量的數據類型的要求以及編程復雜度，統一將中間變量的數據類型定義為32 bit 浮點型數據。本實驗構建二值化網絡的前向傳播與反向傳播算法如算法1 所示。其中，(a0,a*)為輸入批數據與標簽，W為原始全精度參數，θ為批歸一化層的參數集，η為學習率，C為損失函數，L為二值化網絡的層數，?為二值/全精度卷積運算，Binarize(?)為參數的二值化處理，BatchNorm(?)為批歸一化處理，BackBatchNorm(?)為批歸一化處理的反向傳播，Update(?)為相應優化器的參數更新過程以及此優化器規則或人為設定規則的學習率更新過程。

圖6 網絡塊組成結構

算法1BNN 訓練算法

4 實驗及分析

本文設計并構建BNN 完成電磁信號調制識別任務，實驗選取8 種常用數字調制信號對本文方法進行驗證，分別為4ASK、BPSK、QPSK、OQPSK、8PSK、16QAM、32QAM 和64QAM，噪聲環境為加性高斯白噪聲，信號的I/Q 波形域為通用調制基帶信號，波形圖可參考文獻[25]。實驗構建的數據集中，每個信號樣本生成10 000 個采樣點，并利用2.2 節所述方法進行預處理，得到特征增強的星座圖。

數據集規模比例為訓練集:交叉驗證集:測試集=3:2:2。在訓練集中，每個信噪比點下每種調制信號生成3 000 個信號樣本，在測試集與交叉驗證集中每種調制信號生成1 000 個信號樣本。實驗在Windows 10環境下選擇Pytorch 深度學習框架完成3.2 節中設計的二值化網絡的構建。同時，設計具有相同規模的FNN 作為對照組。實驗的GPU 環境為GTX2080。

4.1 二值化網絡訓練分析

本節設計基于BNN 的電磁信號調制識別實驗，考慮到在二值化網絡反向傳播過程中二值化參數的梯度直接傳播給原始參數帶來的梯度誤差，實驗尋找適用于BNN 的訓練優化器。

實驗選擇SGD（stochastic gradient descent）、RMSprop（root mean square prop）與Adam 這3 種常用的優化器，在試驗性數據集上分別對FNN 與BNN 進行訓練，評估其訓練效果。試驗性數據集的調制信號類型、噪聲環境與處理方法均與實驗數據集相同，僅僅將規模調整為訓練集、交叉驗證集與測試集均為每個信噪比下每種調制信號100 個樣本。訓練結果如圖7 所示。

圖7(a)中，實線為損失值變化曲線，對應y軸左側；虛線為準確率變化曲線，對應y軸右側。從圖7(a)中可以看出，在3 種優化器下，2 種網絡在驗證集的準確率均隨著批數據（Batch）的損失值的下降而波動上升，在達到2～3 個訓練周期（Epoch）后，訓練結果都趨于穩定，穩定階段的損失值越低，驗證集下的準確率越高。結合圖7(b)可以發現，FNN在3 種優化器下均可以實現準確率達80%以上，訓練穩定后，損失值由大到小的順序為SGD、RMSprop和Adam，而準確率正好相反，說明Adam 更適合作為FNN 的訓練優化器。結合圖7(c)可以發現，BNN 在SGD 優化器下基本不能完成訓練，而在Adam 與RMSprop 優化器下準確率均可以達到93%以上，其中RMSprop 優化器下的結果要高于Adam優化器，說明RMSprop 更適合作為BNN 的訓練優化器。對比2 種網絡可以發現，BNN 除不能在SGD優化器下完成訓練外，在另外2 種優化器下訓練穩定后，BNN 的損失值均小于FNN，而準確率均高于FNN。由此可以得出結論，BNN 相較于FNN 的訓練難度更高。通過選取更合適的優化器訓練，可以得到泛化性能更強的模型。

4.2 模型的識別效果分析

根據4.1 節的測試結果，本實驗分別為BNN 與FNN 選取合適的優化器（即BNN 使用RMSprop 優化器，FNN 使用Adam 優化器）在實驗數據集上進行訓練。分析其在不同信噪比下對8 種信號的識別準確率，并將其結果與文獻[6,12]進行對比。文獻[6,12]與本文選取的電磁信號的調制類型相同，對比結果如圖8 所示。

圖7 BNN/FNN 在3 種優化器下的訓練過程

圖8 各信噪比噪聲下的結果對比

通過對比分析可以發現，隨著信噪比的提升，4種模型的準確率均呈現上升趨勢。當信噪比大于0 dB時，本文設計的BNN 和FNN 與文獻[12]的識別準確率均達到100%，整體分類性能明顯高于文獻[6]。對比各個網絡的結果可以發現，本實驗的BNN 模型僅在?4 dB 下的準確率低于文獻[12]的結果，在其余信噪比的噪聲下均為最高準確率，由此證明了本文基于BNN 對調制信號識別的有效性；在各個信噪比的噪聲下，BNN 的分類準確率均高于FNN，可以發現在相同規模的網絡結構下，BNN 具有更強的泛化性能。

為了進一步分析BNN 對調制信號的分類性能，本文繪制了模型分類的混淆矩陣，并計算了分類整體的準確率與每個類別下的召回率和精準度，如圖9所示。圖9 中真實標簽與預測標簽交叉對應的區域為分類的混淆矩陣，其中，數字為每個分類下的樣本數量與樣本占測試集的百分比；右下角位置為整體的分類準確率，其代表模型對數據集的綜合性別性能；最下邊一排的其余位置為每個分類的召回率，其代表模型對這個類數據的分類性能；最右邊一列的其余位置為每種分類的精準度，其代表模型預測一個數據為該分類的可信度。從圖9 中可以看出，模型在選定的信噪比范圍內對數據集的綜合識別率為96.1%，對4ASK、BPSK、16QAM 這3 種調制信號實現了100%的識別，而分別在QPSK 與OQPSK 和32QAM 與64QAM 之間產生輕微混淆。另外，模型對于8PSK 信號的分類性能較差，其置信度與精準度都明顯低于其他調制類型，容易與其產生混淆的類別為QPSK 與OQPSK。從整體情況可以看出，BNN 模型可以準確地對低階調制類型進行分類，對不同調制類型的調制信號不易產生混淆，而對相同調制類型下不同階調制信號容易產生混淆。

4.3 模型規模及運行時間分析

建立在BNN 對電磁信號調制識別的可行性基礎上，本文進一步從模型規模以及運行速度兩方面對模型的高效性進行評估。實驗選擇的測試環境為京東AI 的DABNN，其為針對ARM 指令集高度優化的二值化網絡推理框架[24]；選取的平臺為單一ARM 內核、主頻1.5 GHz 的樹莓派4B。

圖9 信噪比為?6～6 dB 噪聲下的BNN 分類的混淆矩陣

實驗將模型文件的大小作為模型規模的評價指標，將模型實際部署后的運行時間作為運行速度的評價指標。為了避免偶然因素影響運行時間的測量，本實驗設計在開機穩定運行30 min 后連續測試100 次，求運行時間的平均數作為測試結果。BNN與FNN 的測試結果如圖10 所示。

圖10 相同規模BNN 與FNN 的模型大小與運行時間比較

通過實驗結果可以發現，FNN 模型文件大小是BNN 的26.16 倍，分析網絡規模可以發現，在二值化層中每一個參數由原來的32 bit 浮點型數據縮減到1 bit，而BNN 中的第一層與輸出層仍然保持全精度層不變，綜合得到26.16 倍的壓縮率是合理的。另一方面，FNN 的運行時間是BNN 的2.37倍，本實驗設計的網絡為7 層網絡，其中5 層為二值化層。模型運行時間的壓縮倍數會隨著二值化層的占比增加而增加。綜合以上結果，相較于FNN，BNN 可以作為更高效可行的電磁信號調制識別方案。

5 結束語

邊緣智能信號識別是6G“萬物互聯”時代的至關重要的一項技術。本文針對該問題，總結了已有的研究成果，提出了一種基于BNN 的信號圖像域智能識別方案。所提方案通過繪制信號的星座圖將信號從波形域轉化為圖像域，進而用BNN 對圖像域信號進行識別。本文以電磁信號調制識別問題為例對該方案進行驗證，在信噪比為?6～6 dB 的加性高斯白噪聲環境下獲得96.1%的準確率，且在不同信噪比下的識別準確率均高于同規模FNN，整體分類性能優于相同問題的已有算法，證明了方案的可行性。其次，實驗將所提方案部署于具有單一ARM 內核、主頻1.5 GHz 的樹莓派4B 平臺上，模型文件僅有166 KB，平均運行時間僅為290.481 ms，證明了所提方案的高效性。

綜上所述，本文提出了一種兼具可行性與高效性的邊緣電磁信號調制識別方案，但是該方案仍具有很多值得提升與研究之處。例如，本文的信號預處理部分利用信號處理的先驗知識，將電磁信號的高維抽象的波形數據具象化為圖像域，實現了對調制信號的特征增強，也增強了數據的可解釋性與可分性，但這種方法會引入大量的參數，如何實現對電磁信號的波形數據進行端到端的智能處理是下一步的研究內容。本文相信BNN 仍然存在網絡參數以及連接的冗余，進一步對網絡結構進行精簡或將得到更為小巧高效的網絡模型；其次，卷積神經網絡自動提取數據中有助于分類的高維特征，但電磁信號的卷積層特征是抽象的，其可理解性難以與計算機視覺問題相比，如何對電磁信號的特征進行可視化或對其機理進行解釋也是未來的研究方向。另外，本文所選用的調制信號類型以及噪聲范圍具有一定局限性，應進一步擴大研究范圍以發現問題，對該方案提出改善。