Benders分解算法求解帶有容量約束的選址問題

郭 宇

（沈陽理工大學，遼寧 沈陽 110168）

1 問題描述

帶有容量約束的選址問題是指，在物流配送網絡中，根據客戶的位置、客戶對產品的需求量以及各配送中心的最大容量，確定配送中心的位置，以及由選定的配送中心發往不同客戶的發貨量，使得總的運輸費用和管理費用達到最小。一般可描述為如下的混合整數規劃：

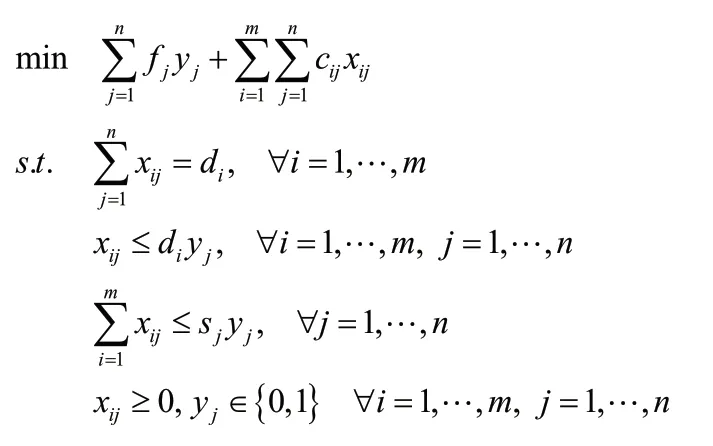
其中：m表示客戶數，n表示備選的配送中心數量，di表示客戶i對某種特定物品的需求量，sj表示配送中心j的最大容量，cij表示將單位物品由配送中心j運往客戶i的單位運輸費用，fj表示建造配送中心j的固定費用。變量yj表示是否開放配送中心j，xij表示由配送中心j運往客戶i的貨物量。

2 算法設計

Benders分解算法是J.F.Benders[1]在1962年首次提出的，目的是用于求解線性混合整數規劃的算法，該算法將線性混合整數規劃分解成只包含連續變量的子問題和只包含整數變量的主問題，首先通過確定復雜變量（即整數變量）將原問題轉化成只包含連續變量的易于求解的線性規劃，再根據對偶理論利用解的的連續變量構造Benders割反作用于主問題，通過連續反復地求解主問題和子問題，最終獲得原問題的最優解。

針對本文中的帶有容量約束的選址問題，設計Benders分解算法如下。

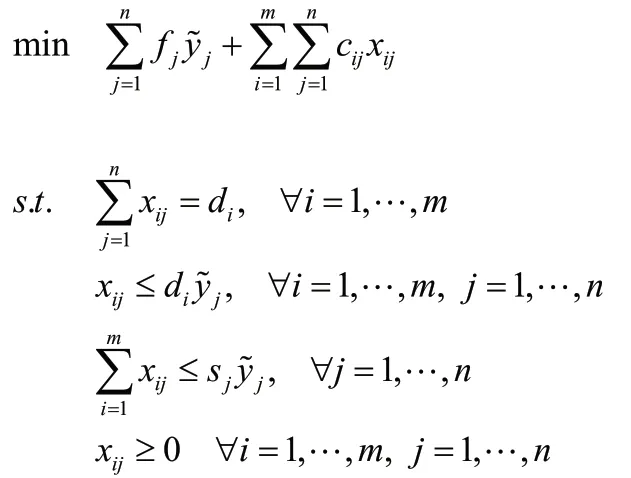
子問題用于求解貨物運輸量的問題。

2）（SPy）的對偶問題可以表示為

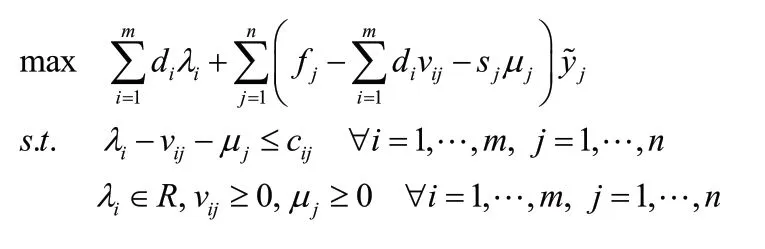
3）根據對偶理論構造Benders割，則可得到如下的主問題（MPT）：

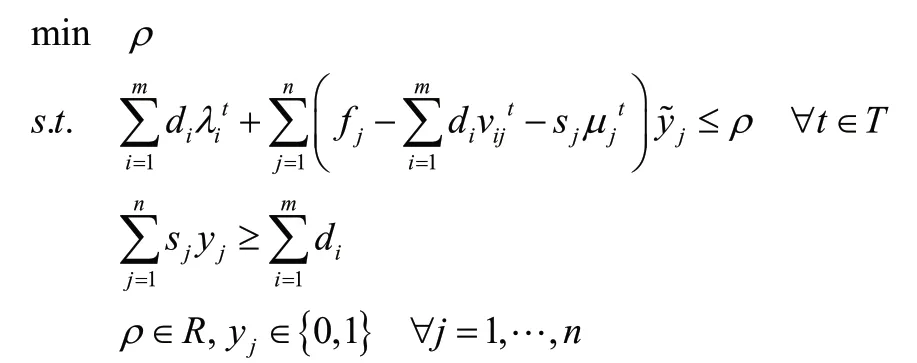
3 算例測試

為測試算法的有效性，選取了Beasley[2]中提供的三組不同規模的問題集進行測試。三組規模分別為：①10個客戶，10個備選配送中心；②20個客戶，30個備選配送中心；③50個客戶，50個備選配送中心。實驗結果表明，本文設計的算法可以在合理的時間內獲得較高質量的近似解。