一類具有時滯的分數階SIS 模型的穩定性分析

蒲武軍

近年來，隨著計算機技術的不斷發展，分數階計算引起了許多學者的關注，并已經成功應用到許多工程技術領域［1-2］，特別是許多應用數學工作者正在用分數階計算模擬現實過程［3-5］.HETHCOTE 討論了一類經典的傳染病模型［6］.CHEN 討論了該模型格動力系統行波解的存在性［7］.鄭義討論了該模型在分數階導數意義下各類平衡點的穩定性［8］.然而，傳染病有一定的潛伏期.如新冠肺炎部分個體潛伏期達14 天之久.因此，討論具有時滯的分數階傳染病模型具有十分重要的意義［9-10］.基于此，本文考慮如下具有時滯的分數階傳染病模型.

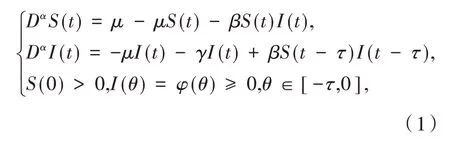
其中：α(0＜α≤1)是方程（1）的階數，S(t)，I(t)分別表示易感者和感染者在時刻t時占總人口的比例，β稱為日接觸率，μ表示單位時間內人口的常數輸入率，γ表示疾病的恢復率，τ表示疾病的潛伏期.

1 預備知識

定義1［11］設α∈R+，函數f(x) ∈L1(0,t)，t＞0，則 函數f(x)的α階Riemann-Liouville 分數階積分定義為：

定 義2［11］函 數f(x) 的α∈(n- 1,n) 階Caputo 分數階導數定義為：

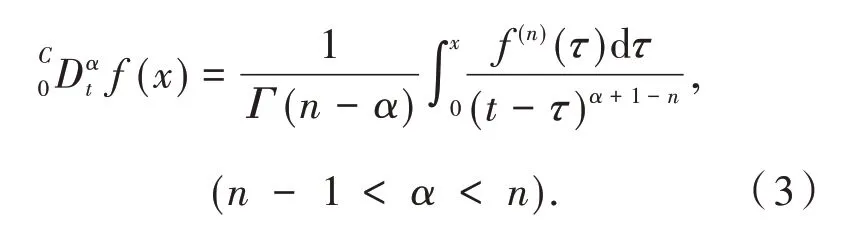
引理1［12］考慮下面具有Caputo 分數階導數的非線性微分方程

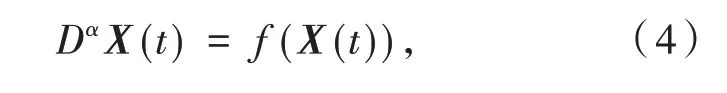
其中：α∈(0,1]，X(t) ∈Rn，則系統（4）的特征方程為|sαE-A|= 0.A為函數f(X(t))在系統（4）的平衡點處的雅可比矩陣.若特征方程限制在-π＜arg(s) ≤π 內的所有特征根均具有負實部，則系統（4）的零解局部漸近穩定.特別地，令sα=λ，則上式變為|λE-A|= 0.此時系統（4）的平衡點局部漸近穩定的充要條件為

引理2［13］考慮下面具有Caputo 分數階導數的非線性時滯微分方程

其中：α∈(0,1],X(t) ∈Rn,τ≥0，則系統（5）的 特 征 方 程 為|sαE-A-Be-sτ|= 0.A，B分別為函數平衡點f(X(t))和g(X(t))在系統（5）的平衡點處的雅可比矩陣.若特征方程限制在-π＜arg(s) ≤π 內的所有特征根均具有負實部，則系統（5）的零解局部漸近穩定.

2 主要結果

2.1 平衡點與基本再生數

由系統（1）的第一個方程可知，當疾病不存在時，隨著時間的變化該地區的總人口數量最終趨于1.因此系統（1）的任意解將進入或停留在區域D中，其中

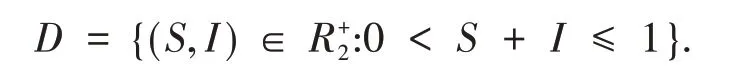
區域D是系統（1）的正不變集.顯然系統（1）總存在一個無病平衡點E0(1,0).利用下一代生成矩陣的方法可得基本再生數R0=

定理1 若R0＞1，則系統（1）存在唯一的地方病平衡點E*，若R0＜1，則系統（1）不存在地方病平衡點.

證明 顯然，系統（1）的地方病平衡點E*應滿足如下方程組

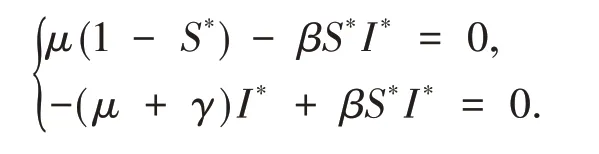
2.2 解的存在性與非負性

定理2 對任意的(S0,I0) ∈Ω，則系統（1）存 在 唯 一 解X= (S,I) ∈Ω，其 中 Ω={(S,I) ∈R2:max{|S|,|I|} ≤K}.

證明 定義映射f(X)= (f1(X),f2(X))，其中

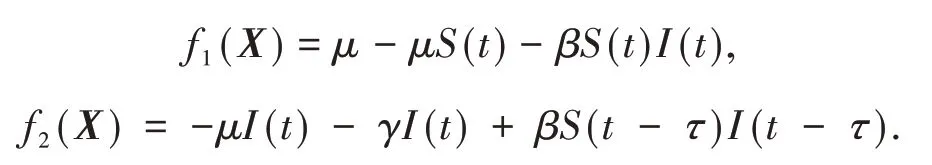
對

因此，f(X)關于X滿足Lipschitz 條件，由文獻［14］的定理3.7 易知系統（1）存在唯一解X(t).

定理3 系統（1）任意始于D的解是非負的.

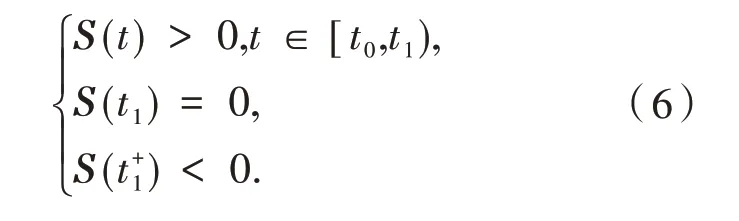
由式（6），并結合系統（1）的第一個方程，易知DαS(t1)|S(t1)=0=μ.根據文獻［15］的定理1 易 得這 與矛 盾.因 此，S(t) ≥0,?t≥t0.同理可證?t≥t0，I(t) ≥0.

2.3 無病平衡點的穩定性分析

系統（1）在無病平衡點E0處的雅可比矩陣為：

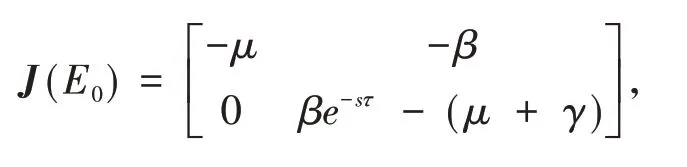
其相應的特征方程為：

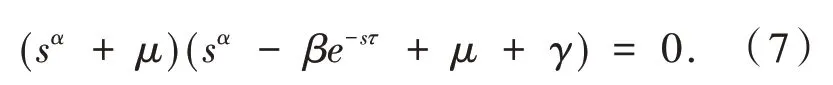
當τ= 0 時，方程（6）簡化為：

定理4 若R0＜1 時，則當τ= 0 時，系統（1）的無病平衡點E0是局部漸近穩定的.

定理5 若R0＜1 時，則對任意的τ≥0，系統（1）的無病平衡點E0是局部漸近穩定的.

證明 若R0＜1 時，則定理4 成立.注意到式（7）的第一個方程不含時滯τ，因此只需考慮第二個方程

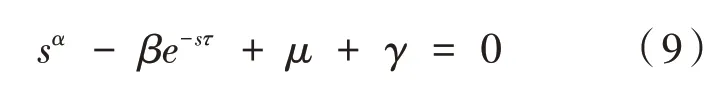
當τ≠0 時根的分布情況即可.設方程（9）存在一對純虛根s1,2=±iw，將其代入方程（9），得

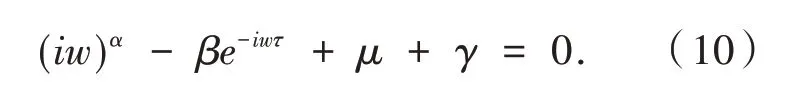
分離實部與虛部得

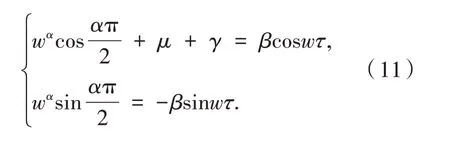
將式（11）兩端平方相加，得

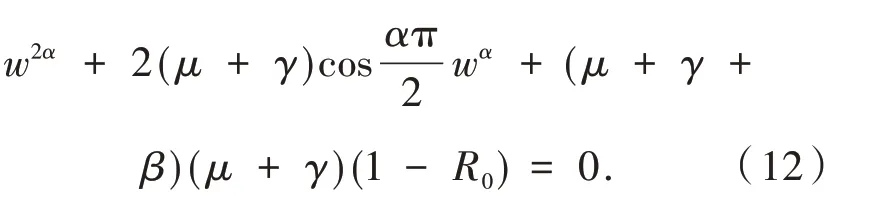
顯然，若R0＜1 時，則方程（12）無正根，即特征方程（9）不存在純虛根.結合定理4 及特征根關于時滯的連續性知，當R0＜1 時，對任意的τ≥0，系統（1）的無病平衡點E0局部漸近穩定.

2.4 地方病平衡點的穩定性分析

系統（1）在正平衡點E*處的雅可比矩陣為：

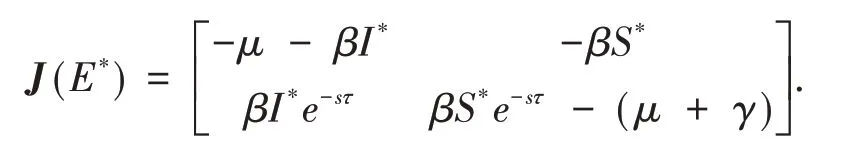
于是，系統（1）在E*處的特征方程det(J(E*))= 0 可寫為：

定理6 若R0＞1，則對?τ≥0，系統（1）的地方病平衡點E*局部漸近穩定.

證明 若R0＞1，根據定理1 知地方病平衡點E*存在.當τ= 0 時，方程（13）簡化為：

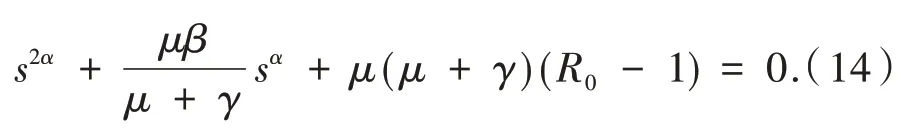
由霍爾維茨判據和引理1 知，系統（1）的地方病平衡點E*局部漸近穩定.

若τ＞0，假 設是式（13）的一對純虛根，并代入式（13），得|ω|2α(cosαπ +isin(±απ)) +|ω|α(μ+

分離實部和虛部，有

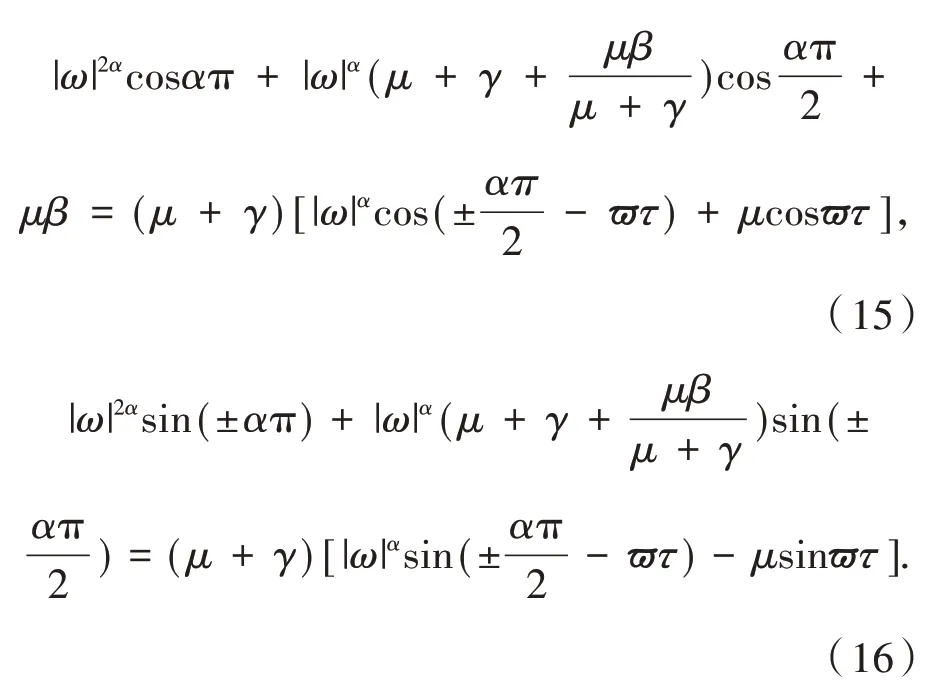
將上面二式平方相加可得

記

顯然，若R0＞1，則方程φ(ω)= 0 不存在純虛根，于是對任意的τ≥0，由文獻［16］中引理1 和性質3，知地方病平衡點E*局部漸近穩定.

2.5 無病平衡點的全局漸近穩定性分析

定理7 若R0＜1，則對?τ≥0，系統（1）的無病平衡點E0全局漸近穩定.

計算L0(t)沿著系統解的關于時間的分數階導數

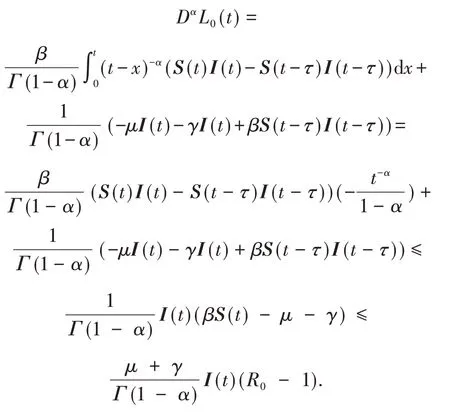
因此，若R0＜1，則DαL0(t)≤0，當且僅當S= 1,I=0時，DαL0(t)= 0.

設M= {(S,I) ∈D|DαL0(t)= 0}.當t→+∞時，M→{E0}所以{E0}是M唯一最大正向不變集，由Lasalle［17］不變原理知，系統（1）的無病平衡點E0在D中全局漸近穩定.

3 結語

本文主要討論了一類具有時滯的分數階傳染病模型的動力學行為，包括該模型解的存在唯一性、非負性，無病平衡點的局部漸近穩定性和全局穩定性，地方病平衡點的局部漸近穩定性，結果顯示時滯不會對該地方病平衡點的局部漸近穩定性產生影響.