隴南市旅游需求組合預測研究

李 娟，席浩元

在以消費拉動未來經濟增長的時代背景下，旅游越來越成為廣大人民群眾物質生活和精神生活的一個重要組成部分.對地方旅游人數的準確預測，可以為當地政府部門制定旅游業發展戰略和宏觀決策提供科學理論依據.由于各省市旅游業發展情況不同，游客人數的預測模型并不具有通用性，已經有很多學者結合某區域游客量數據對該地游客量預測進行了研究.例如基于灰色理論的動態數學模型［1］、基于支持向量（SVM）算法的預測模型［2］、基于灰色線性回歸組合預測模型等［3-5］.

由于單一模型預測的局限性，從而考慮基于Logistic 回歸模型、指數增長模型及多項式擬合模型的組合模型.基于2010—2018年隴南市旅游統計數據，建立了三種單一預測模型及其組合模型，并應用組合模型預測隴南市未來五年（2019—2023年）的旅游人數.

1 三種單一的預測模型

1.1 Logistic 回歸模型

Logistic人口增長模型是指受自然資源、環境條件等因素限制，人口數量在初始階段接近指數增長，逐漸變得飽和時增速變緩，最終達到穩定后增長停止.其方程為：其中：K表示環境能供養的人口總數上界，r表示常數變化率，N( )

t表示t時刻人口總數，N0表示初始時刻t0的人口初始值.

采用分離變量法得式（1）通解為：

式（2）可以進一步標準化為：

其中：a=r，b為與初始值和k有關的量.

1.2 指數函數擬合模型

擬合是以殘差平方和最小為原則，得到的測試函數不一定經過所有的測試數據點.或者說已知某函數的若干離散函數值，通過調整該函數中若干待定系數，使得該函數與已知數據的差別最小.

指數擬合模型為y=eat+b+c.應用最小二乘法待定系數a，b，c.

1.3 多項式擬合模型

多項式擬合即采用多項式函數進行擬合、逼近數據所出現的趨勢.多項式的系數采用最小二乘法進行計算.多項式的次數一般通過已知數據畫出數據散點圖，根據變化趨勢來確定.多項式擬合模型為：

2 隴南市旅游人數預測實證

數據來源于《2010—2018年隴南市國民經濟和社會發展統計公報》，2010—2018年隴南市旅游人數如表1 所示.

從表1 可以看出，隴南市旅游人數呈現歷年來遞增趨勢.本節利用2010—2016年數據建模，使用2017年、2018年數據進行模型檢驗，最后預測未來5年（2019—2023年）隴南市接待的游客人數.

表1 2010—2018年隴南市游客量

根據表1 提供的隴南市歷年游客總數數據，利用MATLAB 數學軟件作出隴南市2010—2016年隴南市旅游人數散點圖，為了避免數據相差太大造成誤差，先將數據處理，年份均減去2009，對應于時間變量t1= 1，t2= 2，…，t7=7.相應人數為321.17、390.78、490.48、614.35、766.24、985、1261.58.

2.1 Logistic 回歸模型的建立

利用MATLAB 軟件編程計算，采用共軛梯度法求解模型，得到模型參數a= 0.2369，b=6.494，c= 159000.故Logistic 模型為：

應用模型（5）計算結果及誤差情況如表2和表3 所示.

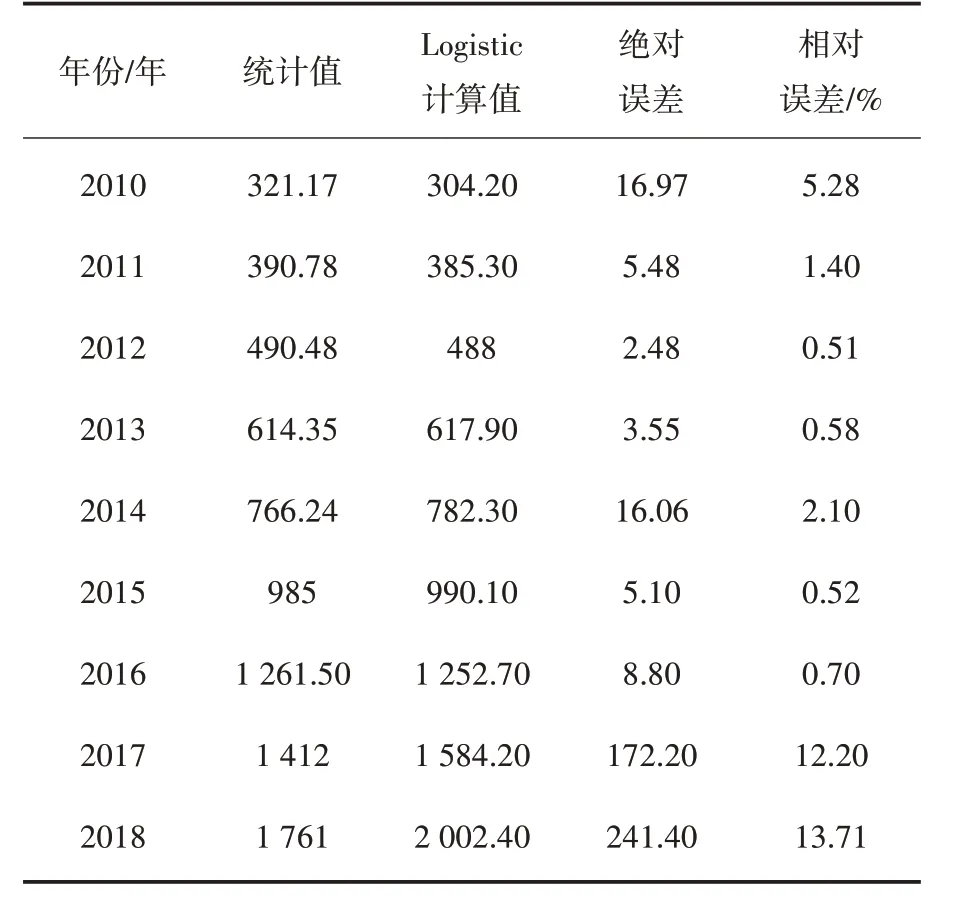
表2 Logistic 模型計算值、絕對誤差、相對誤差

表3 三次多項式擬合模型計算值、絕對誤差、相對誤差

2.2 指數函數擬合模型的建立

對數據應用最小二乘法，采用MATLAB 編程計算，得指數擬合的參數分別為：a=0.2705，b=5.172，c=90.48.于是指數擬合模型為：

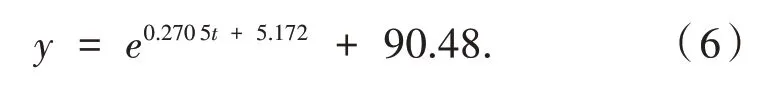
該模型計算結果及誤差分析如表3 所示.

2.3 三次多項式擬合模型的建立

作出散點圖，觀察數據的變化趨勢，采用三次多項式擬合，擬合函數為：

利用最小二乘法計算參數為：a3=1.956，a2=-3.403，a1=72.67，a0=248.2，于是得到三次多項式擬合模型為：

該模型計算結果及誤差分析如表4 和表5所示.

表4 指數函數擬合值、絕對誤差、相對誤差

表5 組合模型計算值、絕對誤差、相對誤差

2.4 基于最小二乘法的組合模型

由表2、表3、表4 可以看出，三種單一的預測模型計算所得擬合數據的計算誤差都比較小，但用來驗證的2017年、2018年的計算數值與原觀測值的相對誤差比較大，均達到了10%以上.為了提高精度，基于上述三種單一模型，建立如下組合模型：

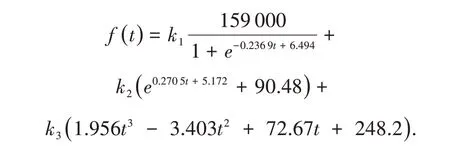
應用最小二乘法計算參數為k1= 0.0002，k2= 0.8634，k3= 0.1364.

于是組合模型為：

該模型計算結果及誤差分析如表5 所示.該組合模型計算所得2017年的旅游人數為1403.3 萬人次，相對誤差僅為0.62%.2018年的旅游人數為1814.9萬人次，相對誤差為3.06%.可見組合模型優于三種單一的預測模型.應用組合模型預測未來五年（2019—2023年）隴南市旅游人數分別為：2354.4 萬人次、3061.5萬人次、3988.1 萬人次、5202.6 萬人次、6794.3萬人次.組合模型擬合及預測圖如圖1 所示.

圖1 組合模型擬合及預測圖

3 模型評價

應用最小二乘法計算組合模型的參數為k1= 0.0002，k2= 0.8634，k3= 0.1364.從參數ki（i=1，2，3）的取值可以進一步看出，k1很小，所以Logistic 模型貢獻最小，多項式參數k2取值也不大，組合模型貢獻最大的是指數函數擬合模型.這正好與表1、表2、表3 計算出的三種單一預測模型的相對誤差結果相吻合.如果考慮模型的簡潔性又使得精度在一定范圍內，可以考慮選擇指數函數擬合模型.

4 結語

本文建立了三種單一的預測模型對隴南市旅游人數進行擬合與預測，在此基礎上，進一步建立了三種單一模型的組合模型對觀測數據進行擬合，采用最小二乘法計算出組合模型的相應參數，進而應用該組合模型進行擬合與預測，計算結果表明，組合模型的計算精度大大提高，其計算結果均優于三種單一的預測模型.

應用組合模型預測2019—2023年隴南市旅游人數的數據顯示，隴南市旅游人數呈現持續增長的態勢.