當深度學習遇到低年級數學

戴湘平

【摘 要】 深度學習過程著眼于學生對所學內容的整體理解，促進學生的知識建構和方法遷移，并有助于學生高階思維的發展，讓學生在解決問題的過程中提高核心素養。對于低年級的小學生來說，他們經歷數學學習的時間很短，思維方式和學習能力等方面皆有欠缺，那么如何在低年級數學教學中落實深度學習呢？本文結合課堂教學實踐進行了分析和探討。

【關鍵詞】 深度學習;經驗課堂;數學思想

為全面深化課程改革，落實立德樹人的根本任務，我們開始了深度學習教學改進項目的研究。“開展小學數學學科深度學習的意義在于：通過學習方式的改變，以學生核心素養為重點，促進學生的整體發展。深度學習過程著眼于學生對所學內容的整體理解，促進學生的知識建構和方法遷移，并有助于學生高階思維的發展，讓學生在解決問題的過程中提高核心素養。”

對于低年級的小學生來說，他們經歷數學學習的時間很短，思維方式和學習能力等各方面皆有欠缺，如何在低年級數學教學中實施深度學習呢？以下是筆者在教學中進行的一些探索。

一、基于學生已有經驗，讓“經驗課堂”促成深度學習

曹培英老師提出：深度學習對教師的基本要求是“吃透教材”“吃透學生”。低年級數學的學習內容相對中高年級要簡單得多，例如二年級上冊“連乘、連除和乘除混合運算”這課，教材設計了“2×3×4=24”和“36÷4×3=27”這樣兩道題作為例題。按照教參的建議，在教學例題時只要出示例題，直接告訴學生該先算什么再算什么就可。

在教學這課時，筆者不禁思考：難道就這樣“直接告訴”嗎？直接告訴，學生除了學到該怎么算之外，還有其他收獲嗎？面對簡單內容，我們該怎么教？教給學生什么？一番思考之后，作出了如下修改：

先出示9道算式，要求學生將這9道算式分類：

46+8-30 4×2×7 32+20-8 5×4+3 6×6÷4

2×3×4 6×5-8 36÷4×38×6+4

學生討論后匯報分類結果如下：

第1類：46+8-30，32+20-8; 第2類： 5×4+3，6×5-8;

第3類：4×2×7，2×3×4; 第4類：6×6÷4，36÷4×3。

根據學生分類，揭示“連乘”“乘除混合”，并出示“連除”：27÷3÷3。

師問：這5類算式中，哪些是我們已經會算的？請你說說它們的運算順序。在學生說完前兩類算式的運算順序后順勢問道：你猜剩下的3類該怎么算呢？

生1：我認為“連乘”和“連除”肯定都是從左往右算，因為它們一個都是乘法，一個都是除法。

生2：我覺得“乘除混合”也是從左往右，因為如果先算后面的，6×6÷4中的6÷4不好算，但從左往右就好算。

師：這些都只是同學們的大膽猜測，究竟對不對呢？咱們還要細心驗證，我們來看看數學家是怎么說的。（出示教學光盤中例題部分的教學）

生：哇！我們太厲害了，居然都猜對了！

繼續完成后面的教學，板書如右圖：

在設計例題教學時，基于學生已有的經驗，用9道算式的分類激活學生的學習經驗，引出本課內容，并讓學生應用已有經驗經歷觀察、分析的過程后，大膽進行猜想，猜測連乘、連除和乘除混合的運算順序，吸引學生全面、深入地參與到學習活動中，激發了學生探究的興趣;通過光盤中“數學家”的解讀進行驗證，讓學生沉浸其中并獲得了成功體驗，豐富了學生的學習經驗。

借助“經驗課堂”式教學方法，這些二年級的學生除了收獲知識之外，還學會了如何思考;知道了學習可以進行“大膽地猜測”，更需要“細心地驗證”;體會了可以將學過的知識遷移到沒學過的內容中。深度學習在這里得到了體現，學生的核心素養得到了提高。

布魯納說過：“教學的目的在于：我們應當盡可能地使學生牢固掌握學科內容。我們還應當盡可能地使學生成為自主而自動的思想家。如此，當學生結束正式學習之后，才有能力獨立地向前邁進。”這里的“自主而自動的思想家”不正是我們踐行深度學習的目的嗎？

二、注重建構數學思想方法，與深度學習相輔相成

深度學習的數學課堂需要學生會思考，思維品質決定學生能否實現深度學習，所以在平常的教學中，我們要注重滲透數學思想，培養學生的思維能力。

低年級的數學學習中已經包含了大量數學思想，其中，“有序思考”就是學生在解決問題時經常要用到的數學思想之一。從一年級開始，我就注重培養學生有序思考的能力，如在一年級教學“分與合”、解決“4-□=□”這類題，在二年級教學《表內乘法》時，就開始滲透有序思考，經過長時間的培養滲透，學生在遇到相關問題時就能做到思維有序、頭腦清晰。

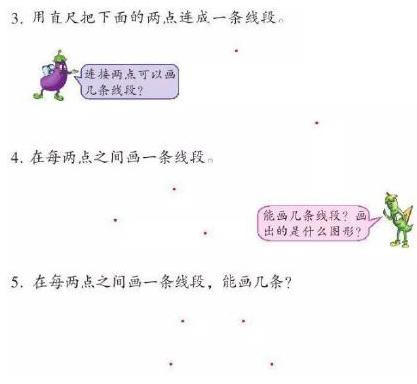
這樣的數學思想能夠有效促進學生提升學習深度。如在教學二年級上冊“認識線段”中“想想做做”3～5題時就體現了出來：

出示3道練習，大部分學生在解決第5題時已經能用有序思考的方法數出線段的總數，為了讓學習更具深度以及挑戰性，引導學生探究：“如果有5個點，像這樣能畫幾條線段呢？”二年級小朋友好勝心強，馬上投入研究，通過畫、數、算，最終找出了正確答案。

接著繼續提問：“6個點呢？不畫能找到答案嗎？這里面有沒有規律呢？”在教師的提示下，那些開始就有序畫線、數線段的學生很快就找到了規律，用“5+4+3+2+1”算出了6個點的線段總數。還有學生自豪地說：“老師，別說6個點，10個點都會算了！”

促進學生深度學習，就是促進學生主動地、專注地、批判性地學習，并將所學知識遷移到新的情境中去嘗試解決新的問題。從這個例子可以看出在教學中注重建構數學思想方法對深度學習的重要性，數學思想能成為深度學習的有力保障，深度學習又豐富了學生數學思想的建構，二者相輔相成。

三、關注學生的“天真錯誤”，將學生從淺層次的學習引向有深度的學習

低年級學生年齡小、學習經驗少，思考問題往往停留在淺層次，不會深入思考，很多時候在數學學習中會采取“依葫蘆畫瓢”的辦法，對大部分知識的認知只是知其然而不知其所以然。例如，在教學“6的乘法口訣”這部分內容時，很多學生會驕傲地說：“老師，我都會算，因為我已經會背口訣了。”當再次追問：“那為什么2×3=6呢？為什么有口訣‘二三得六呢？”孩子們答不上來了。諸如這樣的例子還有很多，所以在設計教學時要充分考慮這些問題。下面以筆者教學二年級上冊“乘加、乘減”的經歷為例具體談談：

首先按例題情境圖順序出示每缸4條金魚的魚缸3個和只有1條金魚的魚缸1個，學生列出算式：3×4+1。

問：3×4+1先算什么？理由是什么？

經過思考，學生能說出先算3×4的理由，看上去掌握得很好。

……

例題教學結束，總結追問：剛才我們研究了“乘加、乘減”算式，為什么它們都要先算乘法呢？

生：因為前面咱們學的“連加連減、加減混合”都是從左往右算的，所以“乘加、乘減”也是從左往右算，應該先算乘法。

從學生的回答情況可以看出，他們對于運算順序的理解還是遷移了前面的經驗，在這段學習中，學生并沒有厘清本質，只是單純地在“模仿”，這樣沒有分析、沒有創新、沒有深層次思考的教學是失敗的。

針對這種情況，筆者立即將后面的教學環節進行了修改：

師：這位同學認為先算乘法是因為要從左往右算，是不是這樣呢？我們繼續研究。

師：還是剛才買金魚的問題，如果生物組先買的是1缸只有1條金魚的，后買了另外3缸有4條金魚的，算式怎么列？

學生列算式：1+3×4。

師：1+3×4也是一道乘加算式，先算什么？

生：先算3×4。

師：不對呀，按照你們剛才的想法，要從左往右依次算，那不是應該先算加法嗎？怎么還是先算乘法呢？

此時在老師的追問下，學生發現了原先想法的錯誤，討論修正后總結出了乘加算式的運算順序。

在本課的教學預設中，筆者根本沒有想到小朋友們會如此“天真”，認為“乘加、乘減”和前面的混合運算一樣都應該從左往右算。幸而在追問下關注了他們的“天真錯誤”，及時修改了教學環節，將情境圖中的魚缸調換順序從右往左逐個出示，引出算式“1+3×4”。雖然教材體系中類似乘法在后的算式要到三年級教學混合運算時才出現，但筆者認為，在這里改編情境圖的順序引入這個算式可以引發學生深度思考，讓學生對運算順序的認知實現由淺到深，能促進學生對運算順序知識的建構，同時也培養了低年級學生批判質疑、敢于探究的科學精神。

在這節課中，雖然學生出現了不正確、有瑕疵的想法，但正是這些不美好，讓我們看到了學生步履蹣跚前行的過程。深度學習，可能就是這樣生長的姿態。

總之，低年級學生年紀雖小，但可塑性很大。低年級數學教學內容雖簡單，但很多時候都需要我們多思考、多研究。當深度學習遇上低年級小朋友，在教師的有效引領指導下，在學生的積極參與下，相信有朝一日，小朋友們定能成長為既具獨立性、批判性、創造性，又有合作精神的基礎扎實的優秀學習者。

【參考文獻】

[1]馬云鵬，吳正憲.深度學習：走向核心素養（學科教學指南·小學數學）[M].北京：教育科學出版社，2019.