談五子棋中的數學

朱旭東

摘? 要：拉普拉斯認為：“在數學中，我們發現真理的主要工具是歸納和模擬。”恩格斯則以為：“數學是研究現實生活中數量關系和空間形式的學問。”

隨著時間的流逝，數學逐漸融入了生活，成為了生活的一部分。“宇宙之大，粒子之微，火箭之速，化工之巧，地球之變，生物之謎，日用之繁，無處不用數學。”就像中國的愛因斯坦華羅庚先生所說，五子棋盤上也隱藏著數學。

關鍵詞：五子棋盤;坐標;幾何

前言：

下棋是棋盤上的戰爭，下棋的過程中隱藏著一些數學的小心機。你要顧全大局，多方面思考，出其不意攻其不備。根據各棋子的坐標，可以幫助我們分析對方棋路，并以此預判對方下一步棋。同時在下棋的過程中有所發現。

在以下探究中，我們將多方面思考，對一組殘局進行研究。探究坐標與棋盤之間的應用，并解決一些關于棋盤的問題。

觀察棋盤：

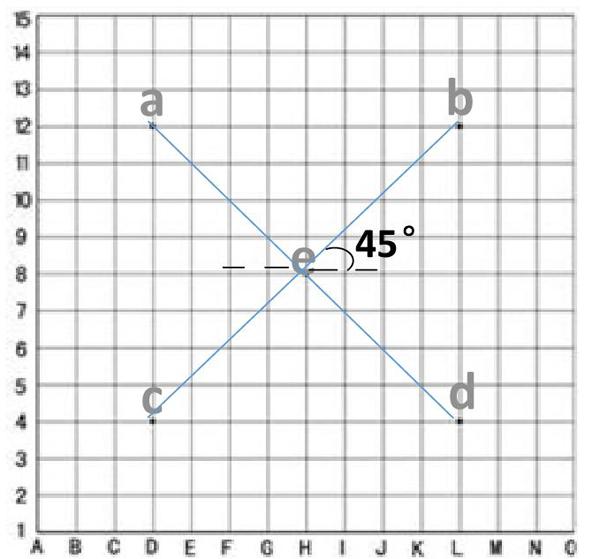
如右圖，為一棋盤。棋盤由橫縱各15條等距離，垂直交叉的平行線構成，在棋盤上，橫縱線交叉形成了225個交叉點為對弈時的落子點。其中直線被稱為陽線，而如右圖所示由交叉點構成的與陽線成45°夾角的隱形斜線（如：l_cb，l_ad等）為陰線。

觀察棋盤，可發現在棋盤上有5個比較特殊的交叉點，這5個點稱為"星"。中間的星也稱天元。我們設它們為a，b，c，d，e。

如圖，a的坐標為（D，12），b坐標為（L，12），c的坐標為（D，4），d的坐標為（L，4），e的坐標為（H，8）。

在下棋時，黑方總是先著棋于天元e，占據棋盤中央的（H，8）相當于包攬了l_ad與l_cb兩陰線五子連珠的機會。將五點相連，得一長方形（棋盤上一個小長方形長2.5cm，寬2.4cm）。

由圖可知，長方形長為：2.5×8=20（cm），長方形寬為：2.4×8=19.2（cm）

∵長方形的面積=長×寬??? ∴S_長方形=20×19.2=384（cm²）

即占據了星和天元后，以天元e為中心面積為384cm²的長方形內五子連珠的機會均為己方所有。

殘局對弈：

這是一組經典的五子棋殘局，可見黑棋主要在以（H，9）為中心集中在一片區域，而白棋則以堵為策，棋路渙散。那么問題來了。

若我方為黑方，對方為白方。問黑方如何落子，可盡快取得勝利？

如圖有四種選擇，①H，11）②（I，11）③（F，8）④（E，7）

①觀察棋局，可發現若下①，黑子立時可完成沖四，如圖一。此時為了不使黑子集滿五子立即獲得勝利。白子必然落子于（H，12），截取所有后路，阻止其沖五。

此時黑方在②著棋沖四，無論白棋在（G，11）堵截還是在（L，11），黑棋只要在兩者中一方著子便能獲勝。

按其他位置著子，需要下超于2顆棋子。對比之下第一步下①可以更快獲得勝利。

拓展提升：

1、在一個平面上，如何用6個圍棋子擺出4行，每行3個的圖形？

若是要擺出4行，且每行3個，那么一共需要3×4=12個，而一共只能使用6子進行擺放，也就是說1個棋子需要當作2個來用，即一子多用。那么就有多種可能，例如，下圖所示的兩種方案。

2、除去對稱或旋轉可以得到的位置，一個棋子在五子棋上有多少種擺法？

比如圖中的1號和2號和29號和50號這四個棋子只能算作一種擺法。

我們可以看到這樣算的話，五子棋盤有15行，15列。整副棋只需看棋盤的1/2×1/2×1/2=1/8即可，我們以右下角的一半為例來看。（如圖二）

即41-49之間的空間39-48及其之間的空間，37-47及其之間的空間，35-46及其之間的空間，33-45及其之間的空間，31-44及其之間的空間，29、43以及最中間天元的位置，那么共有1+2+3+4+5+6+7+8=36種排法。

所以本題的答案是36。

真題實踐：

在7×8的長方形棋盤的每個小方格的中心點各放一枚棋子。如果兩枚棋子所在的小方格共邊或共頂點，那么，稱這兩枚棋子“相連”。現從這56枚棋子中取出一些，使得棋盤上剩下的棋子沒有5枚在一條直線（橫、豎、斜方向）上依次相連。問最少取出多少枚棋子才可能滿足要求？并說明理由。

第一步證明若任取10個棋子，則余下的棋子必有一個五子連珠，即五個棋子在一條直線上依次相連。利用反證法，假設可取出10個棋子，使余下的棋子沒有五子連珠。如圖1，在每一行的前五格中必須各取出一個棋子，后三列的前五格中也必須各取出一個棋子，這樣，10個被取出的棋子不會分布在右下角的陰影部分。同理，由對稱性，也不會分布在其它角上的陰影部分。

第1、2行必在每行各取出一個，且只能分布在（1，4）、（1，5）、（2，4）、（2，5）這些方格。同理，（6，4）、（6，5）、（7，4）、（7，5）所在區域內至少要取出2個棋子。

在第1、2、3列，每列至少要取出一個棋子，分布在（3，1）、（3，2）、（3，3）、（4，1）、（4，2）、（4，3）、（5，1）、（5，2）、（5，3）所在區域。同理，（3，6）、（3，7）、（3，8）、（4，6）、（4，7）、（4，8）、（5，6）、（5，7）、（5，8）所在區域內至少要取出3個棋子。

這樣，在這些區域內至少已取出10個棋子。因此，在中心陰影區域內不能取出棋子。由于紅色方格的這四個棋子至多被取出2個，從而，從斜方向看必有五子連珠。由此產生矛盾。

第二步構造一種取法，共取出11個棋子，余下的棋子沒有五子連珠。如圖2，只要取出綠色方格的棋子，則余下的棋子不可能五子連珠。

在7×8的方格中按1、2、3、4、5的順序依次填入將其編號，可以發現，在該表格中任意一組五子連珠的編號都是1、2、3、4、5各出現一個。其中，56個方格里1出現12次，2、3、4、5均出現了11次。因此，將所有的標號為2的方格中的棋子取出即可（取所有標號為3、4、5亦可）。

結論：最少要取出11個棋子，才可能滿足要求。

總結與反思：

（1）反思：在解題的過程中需要在日常下棋過程中觀察所積累的經驗以及對生活不斷的發現，下棋時也需要運用一定的思維能力與空間想象。在生活中運用數學可以讓一切變得簡單。數學是一種別具匠心的藝術，在棋牌藝術上累計使用，使對弈時，倆者之間更有挑戰。

（2）總結：本文在五子棋中尋找數學并通過真題進行實踐，完成對坐標思維，列舉方法的鞏固與應用。事實上，不止五子棋，其他棋牌中也隱藏著很多數學知識。數學家本質上是個著迷者，不迷就沒有數學，就無法發現生活中關于數學的種種細節。人們總說細節決定一切，數學家就充分證明了這一點。