高維協方差矩陣估計在A股市場的實證研究

任 丹

（上海交通大學 安泰經濟管理學院，上海 200030）

現代組合投資理論是建立在1952年馬科維茨提出的均值-方差模型的基礎之上。馬科維茨運用方差和預期收益率對風險和收益刻畫，企圖在風險和收益之間尋求平衡，在這個過程中，收益率的協方差矩陣起到了分配風險和收益的橋梁作用。隨著現代金融市場的發展，金融數據的維度變得十分龐大，通過歷史數據估計得出的協方差矩陣往往呈現出奇異的特征，因此高維度情況下的協方差矩陣估計成了熱門研究問題。

在傳統研究和應用中，人們通常采用樣本協方差矩陣作為總體協方差矩陣的估計量，但當矩陣的維度變得很大時，估計顯得十分困難。尤其是橫截面維度超過時間維度時，樣本協方差矩陣是奇異的，均值方差模型是不能求解的。同時，估計過程中產生的累積誤差會對最終的估計結果產生影響。為了解決前述問題，學者們提出了許多有效的估計方法，在金融投資實踐中取得了顯著的成果。

1 文獻綜述

高維協方差矩陣估計方法的研究主要集中在以下三個方面：1．基于因子模型的高維協方差矩陣估計，即通過有限的因子來達到降維的目的，得到有效的估計量，該方法在學界和業界均取得了顯著的效果。2．壓縮估計方法，該方法盡可能地保證估計量的特征向量同真實協方差矩陣估計量的關系，通過最小化損失函數來控制估計量的特征值。3．基于橢圓分布的高維協方差矩陣估計方法，該方法假設金融數據服從橢圓分布，建立了一系列性質優良的估計量。

本文首先介紹基于因子模型的高維協方差矩陣估計的一般方法。假設n個因子為Fnt構成的因子列向量為Ft，bt為各個因子上的暴露程度向量，eit為資產的特征收益，則相應的資產配置模型為

單個資產模型（1）整合成多維資產模型便有

假設特質收益et與公共因子Ft不相關，對模型（2）兩邊取方差便有

在模型（3）中，?為資產的協方差矩陣，W為因子的協方差矩陣，Se為特質收益的協方差矩陣，通常假設該矩陣為稀疏的。從估計流程不難發現，有限的因子起到了降維的作用，同時保證了估計得出的協方差矩陣是非奇異的?；谝蜃幽Ｐ偷母呔S協方差矩陣估計方法主要分為兩類：可觀測因子和不可觀測因子。二者的整體框架是一致的，不同點在于因子的刻畫上。

從可觀測因子的研究角度來看，學者認為資產收益率可以由公共因子解釋，比如市場收益率、市值、估值等因子，通過這些公共因子達到降維目的。Sharpe（1964）最早提出了單因子模型，認為股票的收益率可以由市場收益率解釋（CAPM）。Fama和French（1993）認為企業自身因素才是影響資產價格的重要因素，采用市值、賬面市值比和市場收益率作為新的因子對資產定價?？捎^測因子的好處在于因子的易獲得性和可解釋性強。

從不可觀測因子的研究角度來看，研究者提出的最典型方法為主成分估計法（PCA）和極大似然估計。主成分估計法是通過對樣本協方差矩陣進行分析，獲得相應的主成分作為主要的因子。典型地，如Fan（2013）提出了基于主成分的非參估計量——主成分正交補閾值估計量（POET）。但是主成分分析法主要是基于樣本協方差矩陣來完成的，樣本協方差矩陣的特征值和特征向量對與因子相關的假設檢驗起到了約束作用。為了突破此局限，Doz等（2012）將極大似然估計引入高維協方差矩陣估計領域，Bai和Li（2012，2016）完善了此框架，并證明了極大似然估計量的一致性。

壓縮估計方法主要分為兩類：線性壓縮和非線性壓縮。從線性壓縮方法的研究角度來看，給定壓縮目標和樣本協方差矩陣，最小化二者的線性組合與真實協方差矩陣之間的距離，來獲得最優的線性壓縮權重。該方法不考慮具體的因子和因子結構，通過壓縮目標對樣本協方差矩陣進行改進。Ledoit和Wolf選取單指數模型等相關稀疏矩陣和單位陣作為壓縮目標，利用美股數據做了實證研究，發現單位陣的表現效果是最好的。從非線性壓縮的研究角度來看，該方法是控制樣本協方差矩陣的特征向量不變，對特征值進行優化，Leodit和 Wolf（2012，2014a，2015）系統地研究如何將非線性壓縮的不可解轉化為依賴樣本特征值極限分布的理想估計量，再利用前面得出的估計量進行優化分析。

通常的金融研究中，研究者們會假設收益率向量服從高維正態分布，即X∶Nd（m，S），但是金融市場中的數據大多呈現出非正態和厚尾的特征，因此學者們通常假設金融數據服從橢球分布，以此為基礎提出新的高維協方差矩陣估計方法。協方差矩陣可以分解成皮爾遜相關系數矩陣和資產標準差對角陣的乘積，即

問題轉化為對皮爾遜相關系數矩陣和標準差對角陣D的估計，Zhao和Liu（2014）基于這一思路提出了EPIC估計方法。對于皮爾遜相關系數矩陣R的估計，Fan等（1990）提出了正弦變化的肯德爾t估計量，即計算資產i和資產j之間的肯德爾t相關系數，并用正弦函數進行轉換后作為矩陣R的（i，j）元估計。Catoni（2012）提出了均值和標準差的M—估計量，該估計量在厚尾分布中表現出極好的性質，可以作為標準差對角陣D對角元的估計量。沿著這一方向，許多學者提出了新的估計方法，如Liu等（2014）提出的EC2估計法。

由于國內的金融市場發展較國外晚，國內學者對高維協方差矩陣估計的研究是最近幾年才興起的。劉麗萍（2016）將主成分法和門限方法相結合，提出了門限主成分正交補（TPO）估計量，并通過實證發現該方法能提高協方差的估計效率、有效降低噪聲的影響。趙釗（2017）總結了國內外學者對高維協方差矩陣估計問題的相關文獻，發現非線性壓縮方法提高了DKK和BEKK模型的估計效率，在高維協方差矩陣估計方面起到的重要作用。宋鵬、胡永宏（2017）提出了基于Cholesky分解的可預測值因子模型，并同VAR-LASSO方法進行比較，發現其在降維方面的優勢較為明顯且二者的估計誤差接近。

目前國內外學者對高維協方差矩陣的研究已經十分深入，對后續的研究具有重要的借鑒意義。本文的研究是基于Ledoit和wolf的線性壓縮模型，將壓縮目標改為協方差矩陣的另一個估計量，即將距離多個估計量線性組合最近的對稱正定矩陣作為高維協方差矩陣的估計量。本文的創新之處在于克服了Ledoit和Wolf中的線性壓縮估計模型之中必須有一個正定矩陣的限制，并考慮了估計量的稀疏性問題，同時對該方法在資產配置中的實際運用進行了實證研究。

2 模型

Ledoit和Wolf（2003）認為給定樣本協方差陣S和壓縮目標矩陣F，最優的估計量應該是二者的線性組合。定義二次損失函數（總體協方差陣）如下：

最小化二次損失函數（5）便可以得到最優權重a*，但總體協方差矩陣S是未知的，因此Ledoit和Wolf（2003）從統計角度給出了最優權重a*的估計量a*est，故樣本協方差矩陣的最優估計量可以寫成樣本協方差矩陣和壓縮目標矩陣的線性組合：

Ledoit和Wolf（2003）認為樣本協方差矩陣S和壓縮目標矩陣F中至少有一個矩陣是正定可逆的，這樣可以保證最后的估計量W是可逆的。但當壓縮目標矩陣和樣本協方差矩陣均不正定時，最后的估計量便不具備正定性的特征。

假設Sn＋為對稱正定矩陣的集合，借鑒壓縮估計量的思想，假設F和S均為協方差矩陣的估計量，本文想求解距離該凸組合距離最近的對稱正定矩陣作為總體協方差矩陣的估計量，即求解以下優化模型（7），來確定最優的樣本協方差矩陣估計量X*：

當a給定的時候，模型（7）轉化為最近相關矩陣問題（nearest correlation matrix）。最近相關矩陣問題如下：給定矩陣G?Sn＋，求解距離其最近的對稱正定矩陣：

模型（8）已經被很多學者進行了研究。Qi和Sun（2006）提出了高斯梯度下降法來求解模型（8），并取得了顯著的效果。學者們不滿足于模型（8）的求解，因為最佳的協方差矩陣估計量具有一定的稀疏性。因此，在問題（8）的基礎上，Liu等（2014）提出了在目標函數中引入懲罰項來保證解的稀疏性，即

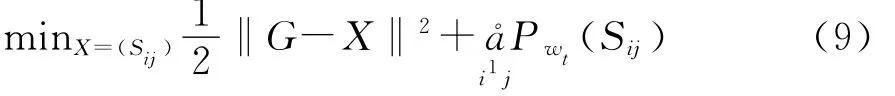
其中，Pwt（x）為懲罰函數，起到控制優化結果稀疏的作用。因此，本文在模型（7）的目標函數中加入l1懲罰函數，使得模型的優化結果具有稀疏性，即

接下來，本文會討論模型（7）和模型（10）的求解方法。

3 模型求解方法

定義無偏估計量G1和G2的凸組合為

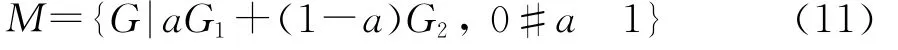
在模型（7）的基礎上，加入條件X3eI，目的是控制優化結果特征根的范圍，因為金融資產始終是存在波動的e，在這里假設最小波動為e。因此，模型（7）便更新為

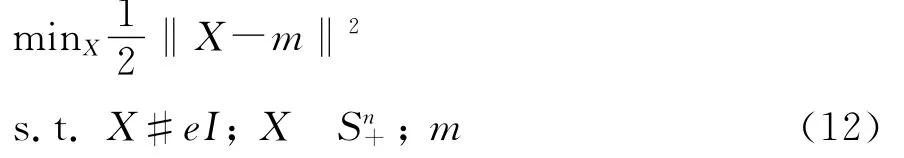
對于模型（12）給定m0，假設m0的n個特征值為l1（m0），…，ln（m0），則m0的譜分解為m0＝?ni＝1li（m0）vivi，那么模型（12）的最優解為X*＝?i＝1max（li（m0），e）vivi′。由于模型（12）的目標函數本身是凸函數，當給定m0的時候，模型（12）存在前述解析解，為了確定最優的a，采用三分法進行求解。模型（12）的目標函數為l（a，X）＝1／2‖X-aG1-（1-a）G1‖2，不斷迭代a，使目標函數的差值直至收斂，具體的迭代算法如下：

模型（12）的迭代解法：

1．初始化：a0＝0，a1＝1／3，a2＝2／3，a3＝1，閾值d；

2．計算相應的目標函數值：l（a1，），l（a2，）；

3．如果l（a1，）＞l（a2，）：

a0＝a1，a3＝a3，a1＝a0＋1／3（a3-a0），a2＝a0＋2／3（a3-a0）；

如果l（a1，），l（a2，）：

a0＝a0，a3＝a2，a1＝a0＋1／3（a3-a0），a2＝a0＋2／3（a3-a0）；

4．循環上述步驟到兩次結果的絕對值小于d時，停止迭代。

在模型（12）中，考慮的是求解距離給定凸組合最近的對稱正定矩陣，但是在實際運用中，優化結果的稀疏性也是必須考慮的重點之一，所以加入l1懲罰方程，便有

給定m0，模型（13）轉化為

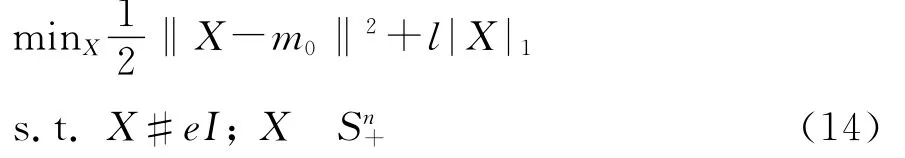
當m0給定的時候，問題就轉變為Xue（2012）研究的問題，其求解方法主要是可選方向迭代算法（alternating direction method），Xue（2012）引入新的變量，將模型（14）改寫成如下形式，即

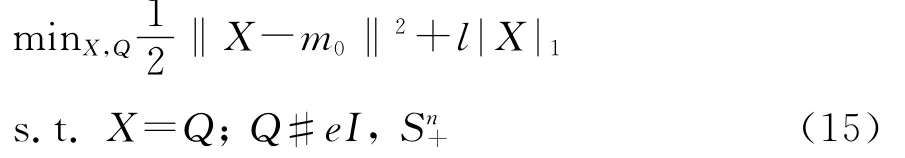
Xue為了求解該問題，采用矩陣形式的拉格朗日方法，即寫出模型（15）的拉格朗日方程，便有

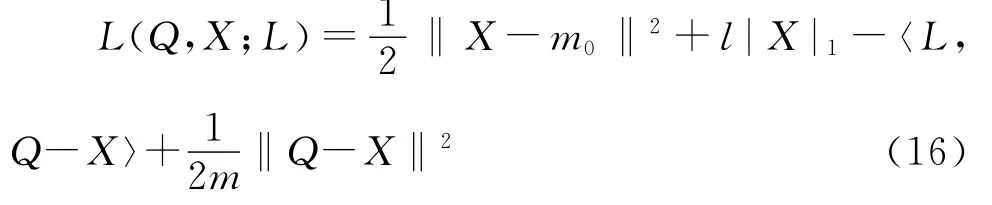
對于模型（16），Xue建立了可選方向迭代算法（alternating direction method），并證明了該算法能收斂到最優的解以及解具有良好的統計性質，求解的算法步驟如下：

模型（16）的迭代解法：

1．初始化：m，X0，L0；

2．第步迭代過程如下：

（1）求解Qi＝（Xi＝m Li）＋；

（2）求解Xi＋1＝｛S（m（m0-Li）＋Qi＋1，lm｝／（1＋m）；

（3）求解Li＋1＝Li-（Qi＋1-Xi＋1）／m；

3．循環上述步驟至收斂。

上述S為閾值函數，對矩陣的非對角元進行控制，在給定矩陣G時，具體形式如下：

對于模型（14），結合上面可選方向理論算法以及f（a，X）是［0，1］′Sn＋上的凸函數，運用三分法求解相應的結果，具體算法步驟如下：

模型（13）的迭代算法：

1．初始化：a0＝0，a1＝1／3，a2＝1及閾值d；

2．運用可選方向理論算法求解：f（a1，X*1），f（a2，X*2）；

4．循環上面的步驟到兩次結果的絕對值小于d時，停止迭代。

附錄里給出算法（13）的收斂性證明，但是模型（13）的求解方法屬于暴力求解算法，模型求解速度慢。因此，本文對于模型（13）只做理論上的探索，不考慮進行實證分析。

4 實證

本文實證數據來自已有的A股數據，時間跨度為2014年1月1日至2017年12月31日，剔除節假日，實際交易日共977天。本文采用最小方差模型來衡量估計出的協方差矩陣的優劣。最小方差模型是指通過最小化風險獲得投資組合中的資產權重，然后根據求出的權重進行組合投資。求解帶懲罰項的協方差估計模型具有極大的計算成本，因此本文的實證部分不進行探討，故只考慮不帶懲罰項的協方差矩陣估計模型。

假設估計樣本協方差矩陣的時間窗口長度為T，利用2T的數據估計出兩個協方差矩陣，再用不帶懲罰項的模型求得相應的協方差矩陣估計S。為了檢驗協方差矩陣估計的優劣，本文采用的模型為最小方差模型，通過最小化波動率來獲得全市場股票的投資權重，模型為

其中，q為資產組合中資產的權重，S為通過前述算法得到的協方差矩陣。根據模型（18）所求權重構建投資組合，并考慮該投資組合在未來一年里的收益曲線，計算相應的年化收益率Rt、方差st、夏普比率ST t。將時間由t變成t＋1，重復前面的步驟，獲得年化收益率Rt＋1、方差st＋1和夏普比率SRt＋1，這樣便可以得到年化收益率序列、方差序列和夏普比率序列。

取窗口長度T為100、200、300天，得到上述不同序列，計算相應指標的均值得到表1結果。

從年化收益的角度來看，不同周期下的估計模型對應的年化收益率均值均高于基準指數的年化收益均值，二者比值的變動區間為［3．13，3．23］；從波動率的角度來看，二者波動率比值的變動區間為［0．95，1．17］；從夏普比率的角度來看，二者夏普比率比值的變動區間為［2．48，2．93］。以上三個指標的比較表明，基于估計模型的資產組合表現比基準組合更加優異，能夠獲得超額收益，本文的基準組合為上證綜指。

表1 不同周期下的評價指標結果

表1結果是從均值角度出發來進行比較的，不能充分反映每個指標在時間維度上的變化情況，因此本文繪制了不同指標隨著時間變化的曲線，得到的結果如圖1、圖2、圖3所示。

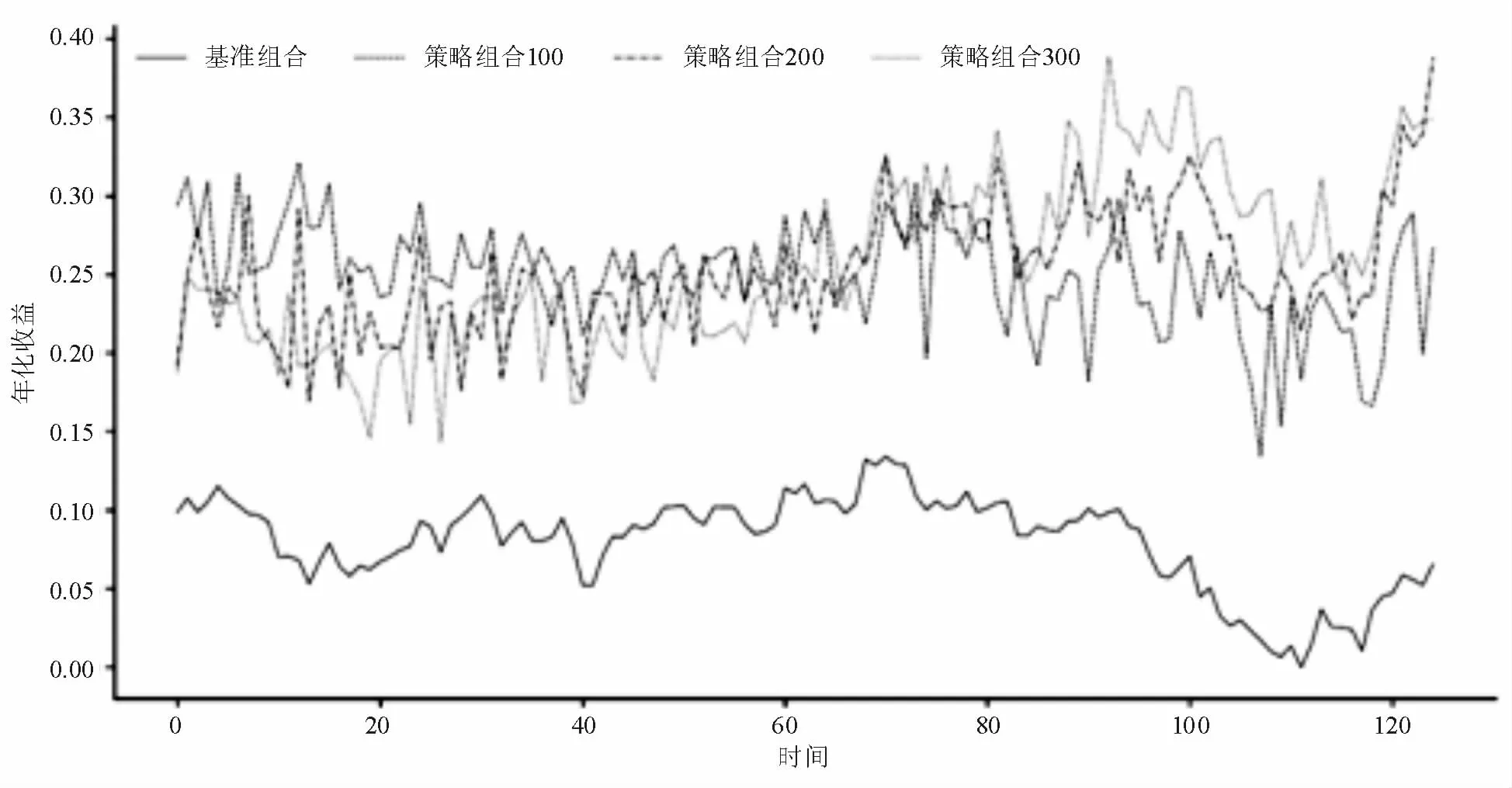
圖1 不同組合年化收益率變化曲線

圖2 不同組合波動率變化曲線

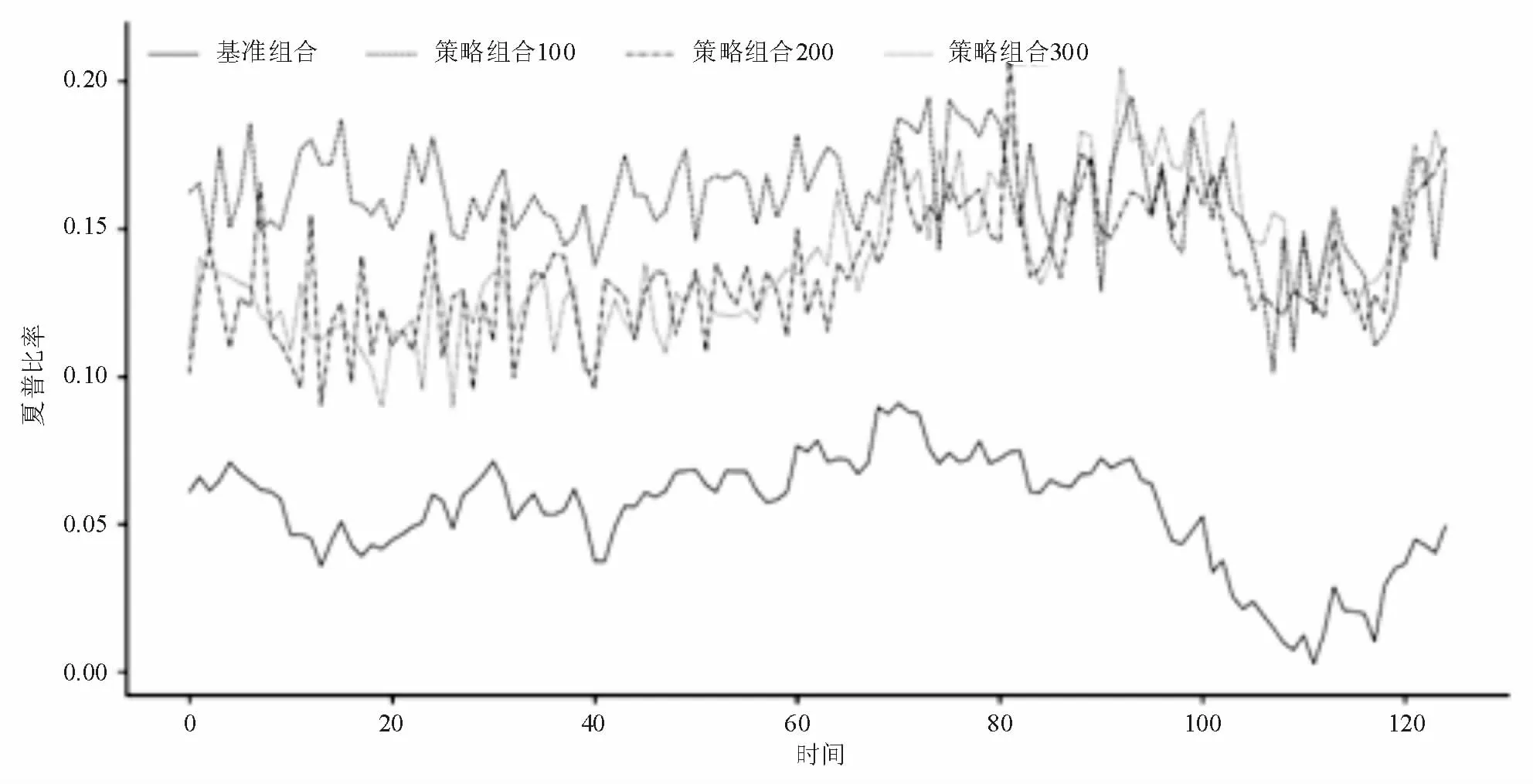
圖3 不同組合夏普比率變化曲線

圖1 的年化收益率曲線表明估計模型的年化收益率是高于基準的年化收益，圖2的波動率曲線表明估計模型的風險暴露程度在絕大多數情況下是高于基準的，圖3的夏普比率曲線表明估計模型所獲得夏普比率是高于基準的夏普比率?？偠灾?，基于估計模型的資產組合與基準資產組合相比較，其在承擔更多風險的同時，獲得了更高的資產收益，且對風險分散十分有效，單位風險所獲得的收益更高。

5 結論

隨著金融市場的發展，金融產品的種類越來越多，金融數據呈現出爆炸級的增長態勢，這給傳統的資產配置模型帶來了新的挑戰——資產維度超過時間維度導致樣本協方差矩陣奇異問題，因此如何有效地估計高維協方差矩陣引起了研究者們的極大興趣。本文回顧了高維協方差矩陣估計領域的研究成果，對不同的研究思路進行了總結。

本文的研究主要是在Leodit和 Wolf（2003）的壓縮估計量的研究成果基礎上展開的，從運籌優化的角度出發，提出了新的估計方法，即尋找距離多個無偏估計量的凸組合最近的對稱正定矩陣作為高維協方差矩陣的估計量。按照對優化結果稀疏性的要求，本文討論了兩種估計模型：1．不帶懲罰項的模型；2．帶懲罰項的模型。對于上述兩種模型，本文給出相應的解法和解法的收斂證明。在理論部分之后，本文結合A股的數據對不帶懲罰項的模型方法進行了實證研究，即基于不帶懲罰項模型求出協方差矩陣的估計量，采用最小方差模型構建投資組合，獲得相應的年化收益率序列、波動率序列和夏普比率序列。通過與基準組合的比較發現，該方法相對于基準帶來了顯著的超額收益，取得了較好的投資效果。