相干聲線跟蹤理論中的周期界面迭代散射仿真方法?

楊 勃 徐祿文 王海濤 陳建明 徐大然

(1國網重慶市電力公司電力科學研究院 重慶 401123)

(2西北工業大學航海學院 西安 710072)

(3國網重慶市電力公司信息通信分公司 重慶 401121)

(4重慶市送變電工程有限公司 重慶 400039)

0 引言

聲場仿真預測是聲學領域中的一項重要研究內容，在噪聲控制、聲品質設計以及聲環境監測等應用中均可發揮重要的作用。室內環境中的聲場仿真受聲波反射因素的影響，相較于自由場環境下的仿真具有更高的復雜度，特別是對于戶內變電站主變室等低頻噪聲突出且噪聲分布頻段較寬的室內環境，其仿真還需要對干涉、衍射等波動現象進行模擬，對仿真方法提出了更高的要求；另外，在戶內變電站主變室、大型廳堂等場所中，常存在著較大范圍的周期排列結構，例如設備散熱器、通風百葉窗、聲學擴散體等，這些界面上的聲散射具有較強的規律性[1?2]，其模擬準確性對于最終的聲場仿真精度也起到重要的限制作用。因此，發展一種能夠對周期界面聲散射進行準確模擬，且具有寬頻高精度的聲學仿真方法，對于室內聲學設計、噪聲控制、聲學監測等應用的支撐具有重要的意義。

經典的聲場仿真預測方法主要可以分為波動聲學方法、統計聲學方法以及幾何聲學方法3類。3類方法目前都有較為成熟的研究，但都存在一定的應用限制。其中波動聲學方法主要適用于低頻段聲場仿真，常見方法包括有限元法(Finite element method,FEM)、邊界元法(Boundary element method,BEM)等。波動聲學方法通過求解波動方程而獲得聲場分布結果，是一種具有嚴格數學理論支撐的仿真方法，可以獲得聲場分布的精確解。但是，由于波動聲學方法需要對空間進行網格離散化處理，受網格尺寸與波長關系影響，當處理較高頻段的聲場仿真問題時，會造成計算規模的急劇上升，特別是當空間中包含周期界面時，需對所有周期子結構進行非常細化的空間離散處理，會進一步影響計算精度并嚴重降低計算效率[3]。統計聲學方法通常特指統計能量分析法(Statistic energy analysis,SEA)，此方法在高聲模態密度條件下分析功率流實現對聲場的預測，僅適用于高頻仿真問題，而在低頻段無法適用，而且在實際應用中，統計能量分析法所需參數較為復雜且不容易獲取，例如各類耦合因子等，因此應用受限較多[4]。幾何聲學方法是另一類重要的聲學仿真方法，是指通過模擬聲波物理傳播過程或物理規律而實現對聲場仿真的方法，主要包含聲線跟蹤法(Ray tracing method,RT)、虛聲源法(Image source method,ISM)等。其中聲線跟蹤法由于具有物理描述直觀、建模簡易等特點，自其在20世紀60年代被提出后就獲得廣泛關注[5]。

早期的聲線跟蹤法中，由于聲線無法模擬聲波的衍射、干涉等波動現象，導致其只能適用于高頻聲場仿真。為了在簡便的幾何聲學框架下提高對低頻段聲場的模擬精度，Gensane等[6]提出了一種能考慮不同反射波之間聲壓干涉疊加的干涉模型，并將其應用于幾何聲學方法之中，以提高低頻仿真精度；之后，Lemire等[7]在對點聲源于封閉空間內的聲傳播研究的基礎上，提出了相干幾何法，大大提高了幾何聲學方法在低頻段的仿真精度。而且，由于無需對空間幾何模型進行頻率相關的模型細化，在計算效率方面相較于波動聲學方法具有更加明顯的優勢，因此，相干幾何法已成為涵蓋低頻仿真精度要求的全頻段聲學仿真常用方法。

雖然相干幾何法目前已成為寬頻段聲學仿真的一種常用方法，但是在復雜聲散射存在的情況下，例如周期散射界面存在時仿真精度仍有不足，主要體現在低頻段精度差，其原因是：在低頻段，聲波在周期結構表面實際并不會發生明顯散射，但是傳統相干幾何法中的聲線會受周期結構幾何形狀影響而向無規方向反射，導致聲場趨向于擴散場，與實際情況產生偏差。

針對周期散射界面存在條件下的寬頻空間聲場仿真問題，本文發展了一種基于聲線迭代散射模型的相干聲線跟蹤法。此方法以經典的相干聲線跟蹤法為基礎，在周期散射結構界面反射過程中，聲線將會在散射作用下發生迭代分裂，通過格柵方程預判結構尺寸與波長的關系，給出子聲線的反射方向，并通過散射系數估計不同子聲線反射后的能量；同時，借助于散射模型的引入，可將復雜的周期結構等效為更為簡便的模型，從而降低了幾何建模難度及運算時間。與邊界元法及傳統相干幾何法的比較驗證了此模型在寬頻段，特別是在傳統幾何法精度較差的低頻段，具有較高的仿真精度。

1 基于聲線迭代散射模型的相干聲線跟蹤法

1.1 聲線迭代散射模型

在實際空間環境中，常存在各類周期結構，例如戶內變電站主變室中的散射設備、大型音樂廳中的周期擴散體、各類廠房空間中的通風百葉窗等，均可視為周期結構。假設一包含周期結構的室內環境如圖1所示，其中S為聲源，R為接收區域，Γ為包含周期結構的壁面。

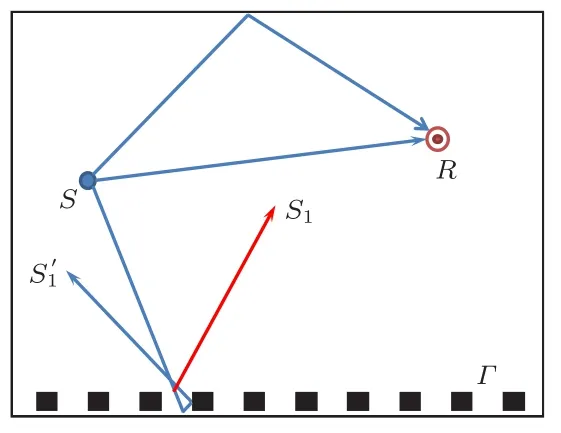
圖1 包含周期散射界面室內環境示意圖Fig.1 The schematic of room environment containing the periodic scattering surface

在聲線跟蹤法中，所有頻段的聲波均采用聲線的形式模擬。對于傳統的相干幾何法，當空間中存在周期結構時，低頻聲線可能會受周期結構的輪廓影響而發生如圖1所示的S′1方向的反射。但實際上，當低頻聲波波長較大時，周期結構不會對低頻聲波產生散射，即低頻聲波將以鏡面反射的方式與界面發生作用，如圖1所示的S1反射，此時傳統的相干幾何法由于對聲線方向模擬不準確，導致提高了聲場的擴散性，造成精度下降。針對此問題，本文發展了一種聲線迭代模型，此模型中，將周期結構在幾何上進行簡化，同時當聲線在周期結構散射界面上發生散射時，將依據周期散射定理發生分裂，分裂的形式與頻率、周期結構尺寸等因素密切相關，以下為模型的具體推導。

假設一根聲線入射到具有周期輪廓的散射體上，首先僅考慮聲線在周期結構垂直切面xOy內的情況，如圖2所示。散射體的單元周期長度為L，凹槽長度為l，高度為H，入射波的聲壓可表示為

式(1)中，θi為入射角，k=2π/λ為波數，λ為波長。與光柵類似，周期型的聲學散射體同樣具有可用光柵方程所表示的周期散射效應，在xOy平面內，散射波的階次及方向可根據周期散射定理求得[8?9]：

式(2)中，θs為散射角，λ為入射波的波長，n為散射波的階次，n=0即代表鏡面反射波。

式(2)表明，當一束聲波入射到周期散射界面上時，會被界面散射為多束反射波。由于需要滿足?1≤sinθs≤1的條件，因此散射波階次n的取值會受聲波頻率、周期結構尺寸以及入射角度多重因素影響。當聲波頻率較低時，波長較大，散射波階次較低，從而反射波的數量較少，但至少會有一束鏡面反射波；而當頻率較高時，散射波階次會較高，反射波的數量也會相應較多。依據此理論，本文提出了聲線迭代來模擬聲波在周期結構表面上的散射作用。此算法的核心思想是將圖2中邊界處的周期結構視為平面結構，這樣可以降低建模的難度，也降低跟蹤過程中的界面處理復雜度，當聲線入射到周期結構上時，聲線會依據式(2)迭代分裂為多根子聲線，此后仍按照經典方法對各個聲線繼續跟蹤。

圖2 入射聲波在周期散射界面散射示意圖Fig.2 Scattering of sound waves incident on the periodic surface

聲線經過周期結構界面散射后，子聲線的數量與n的取值相關，其中第n階子聲線的散射方向為

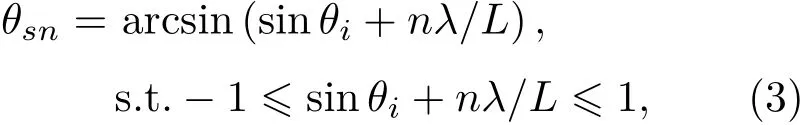
根據此散射方向即可得到此子聲線跟蹤方向的方向向量。

然后，將上述xOy平面內的入射情況拓展到三維情況，如圖3所示，當聲線在xOy平面以外入射到周期結構上時，將其首先投影在xOy平面以內，如圖3中紅色虛線所示，求解入射聲線與其投影夾角γ；然后，按式(3)確定散射子聲線在xOy平面內的反射角θs；以此為基礎，確定xOy平面以外的實際散射子聲線，其自然坐標系下的反射角度通過(θs,r)求得，γ為反射子聲線與其在xOy平面投影的夾角，等于入射聲線與其在xOy平面投影的夾角γ。

圖3 三維空間內的入射聲波在周期界面散射示意圖Fig.3 Scattering of sound waves incident on the periodic surface in three dimension space

1.2 相干聲線跟蹤

通過上述方式確定散射子聲線的反射角度后，即確立了周期結構的聲線散射模型，此后可采用經典的相干聲線跟蹤法完成所有聲線的跟蹤以及統計。對于每一根聲線及其子聲線，跟蹤其傳播路徑，當其達到所設置的測點時，即將其記錄，若一直未到達測點，則在能量低于某一閾值后對其停止跟蹤。最終，在測點處所形成的聲場可表示為

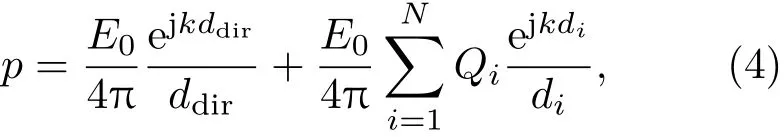
式(4)中，等式右側第一項表示直達聲的貢獻，第二項表示混響聲的貢獻，其中E0表示聲源的源強，ddir表示聲源到測點的直達距離，di表示到達測點的第i根聲線所經過的距離，j為虛數單位，N表示所有到達測點處聲線或子聲線的數量，Qi為聲線從聲源到達測點之間經過的所有界面的聲反射系數，可以由聲線傳輸路徑中每次聲反射對應的單次反射系數依次相乘得到：

式(5)中，M為聲線由聲源到測點之間所經過的反射次數，Qm為每次反射的反射系數，在Lemire相干模型中，利用無限大界面上球面波反射場的近似解來表示，由于聲線在周期結構界面上有可能會發生散射，因此此處將其定義為傳統反射系數與某階散射系數的乘積：

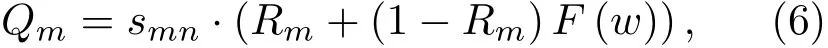
式(6)中，smn為聲線發生第m次反射時第n階散射波的散射系數，即可確定每一個子聲線在新的傳播路徑中所攜帶的初始能量。散射系數的計算值可根據周期結構中一個子單元凹槽的性質，通過有限元方法求解[10?11]，當周期結構的輪廓為矩形結構時，可采用更為簡便的直接估算方法[12]得到其散射系數，此處散射系數的計算也表明，本文所推導的迭代散射模型實際上可適用于具有任意輪廓的周期結構的情況；Rm為第m個反射面上的平面波反射系數，表達式為

式(7)中，θm表示聲線入射到第m個反射面上時與其法線的夾角，βm表示第m個反射面的法向比聲導納。式(6)中，F(w)為界面損失因子，其表達式為

式(8)中，erfc(·)為比例輔助誤差函數，而w為數值距離參數，與聲線所經過的距離、入射角以及相應的邊界有關：

通過上述過程，即可實現對空間內的相干聲線跟蹤。

1.3 適用頻段設定

本文所發展的散射模型一個關鍵處理是在界面上按照散射性質將原始聲線進行迭代處理，在此過程中，原始聲線有可能經過反射后會迭代為多根子聲線，此處分析了聲線數量增長對計算效率的影響。

在傳統的相干幾何法中，選定一根聲線，假設此聲線不被吸收，當經過m次反射后，其能量衰減到限定能量值以下時，即停止對這根聲線的跟蹤。此過程可以表示為

式(10)中，E0為聲線初始攜帶能量，ET為跟蹤過程中的限定能量值，α為壁面的吸聲系數，m為反射次數。對于這根聲線，從其發出到能量過小截止跟蹤后，其跟蹤總次數為

式(11)中，?{·}表示取大于內部函數值的最大正整數。

對于本文方法，假設一個選定聲線每次反射都會發生迭代，迭代后的數量假設為固定值β，即一個聲線會分裂為β根子聲線；且每根子聲線所攜帶的能量相同，即聲線反射后的能量可以平均分配在每根子聲線上。此時對于最終的一個子聲線，其停止跟蹤的過程可以表示為

式(12)中，各符號意義與式相同。根據此式，m值可表示為

對于選定初始聲線，由于每次反射后均會變為更多的子聲線，是一個等比增長的過程，因此，其跟蹤總次數為

通過一特例對跟蹤次數進行對比。假設限定能量值與初始能量值之比為0.2，那么在吸聲系數從0.1～0.5變化條件下的跟蹤次數如圖4所示，其中本文方法每次反射后的迭代子聲線數量β分別為2、3。

圖4 不同方法的聲線跟蹤次數統計Fig.4 Statistics of ray tracing times in different methods

從圖4所示跟蹤次數來看，本文方法總體上相較于傳統相干幾何法會產生較多的跟蹤次數，特別是當較大且吸聲系數較小時，跟蹤次數會嚴重影響計算效率。

為了能夠兼顧計算精度與計算效率，依據室內聲學理論[13]，本文對散射模型的使用頻段進行了限定，適用于迭代模型的頻段為

式(15)中，T為空間的混響時間，V為空間體積。根據室內聲學理論，當頻率高于此頻率時，聲場將以擴散性質為主，此時，傳統的相干幾何法也可以得到較為準確的結果。

2 數值驗證

為了驗證本文所發展模型的正確性，在一個空間中進行了仿真驗證試驗。此空間的尺寸為2.6 m×2.2 m×2.0 m，由于尺寸較小，會發生明顯的波動效應，以此來驗證本文方法對于低頻波動效應模擬的正確性。在其一個壁面上布置有矩形輪廓周期結構，周期結構輪廓的周期長度L為0.2 m，高度H為0.2 m。本算例中，所有界面的聲阻抗設置為80ρ0c0，即法向比聲阻抗為80。算例中設置了一個點聲源，其位置為圖5(a)中橘色圓點所示的(2.4,0.2,0.2)m處，另外設置了9個測點，坐標分別為(0.6,1.8,0.3)m、(0.6,1.6,0.3)m、(0.6,1.4,0.3)m、(0.6,1.8,0.7)m、(0.6,1.6,0.7)m、(0.6,1.4,0.7)m、(0.6,1.8,1.1)m、(0.6,1.6,1.1)m、(0.6,1.4,1.1)m。

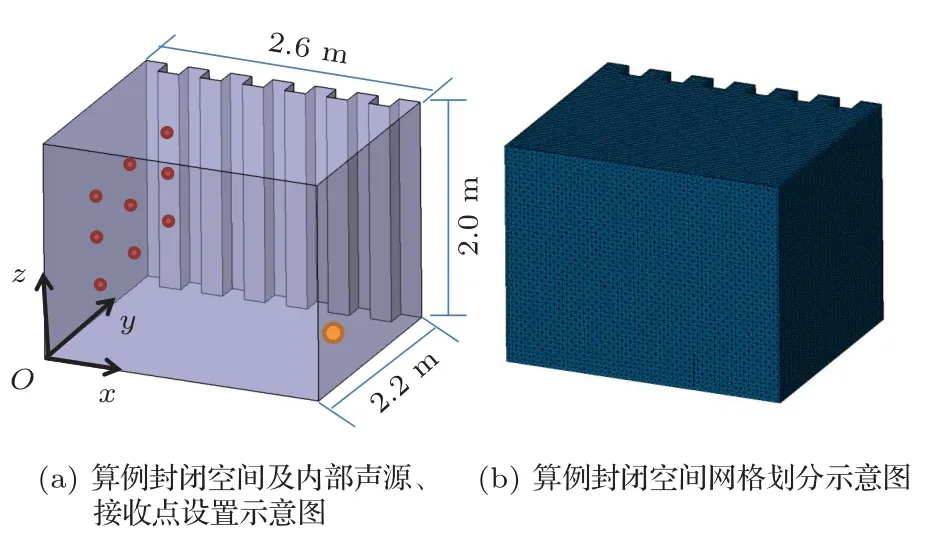
圖5 算例1封閉空間及其網格劃分示意圖Fig.5 The schematic of room environment 1 and its mesh for FEM

此算例首先運用Virtual.Lab軟件的有限元法完成了計算，網格尺寸為40 mm，如圖5(b)所示。根據有限元法網格應滿足上限計算頻率對應波長1/6的經驗定理，此網格條件下，有限元法可達到的上限計算頻率為1416 Hz。為了保證參考方法的準確性，本文選擇1000 Hz作為上限對比頻率。此外，還利用傳統的相干聲線法計算了聲源到所有測點的頻率響應。經過計算，有限元法、本文方法以及傳統相干幾何法在30～1000 Hz所得到的頻率響應如圖6所示，此處給出了測點1處的對比結果。

圖6所示的頻響曲線對比表明，相較于有限元法，傳統相干幾何法在低頻段存在較為明顯的誤差，而本文方法則具有更高的精度。其中，在400 Hz以內的頻段，本文方法所得到的結果與有限元法的結果存在細微的頻率偏移，即所得模態頻率與準確的模態頻率存在一定的誤差，但是在頻率曲線的結構方面吻合度較高，而傳統相干幾何法則除了較為明顯的頻率偏移外，曲線的幅值與有限元法結果也存在一定誤差，這說明在周期結構存在的空間內，本文方法相較于傳統的相干幾何法在低頻段的精度上有較大的提高。在400 Hz以上的頻段，本文方法以及傳統相干幾何趨向于與有限元法結果一致，誤差均較低。此對比說明當空間內存在周期類型結構時，傳統相干幾何方法由于未能準確地模擬周期結構的散射特性，導致其誤差較高，而本文方法對于散射的處理則更符合實際情況，具有較高的精度。

圖6 測點1處不同方法的頻率響應對比Fig.6 Comparison of frequency responses of different methods at measuring point 1

為了分析所有測點處的誤差，統計了9個測點處的模態頻率偏移平均誤差。需要說明的是，此處之所以主要對比模態頻率的誤差，是因為在低頻段模態頻率的位置是一項基礎評價指標，只有當模態頻率處于同一位置時，不同方法才可以比較幅值的關系，否則會因為頻響曲線在頻率軸上的偏移造成幅值無法比較。本文使用式(16)方法統計了本文方法以及傳統方法相對于有限元法的模態頻率平均誤差，結果如圖7所示。

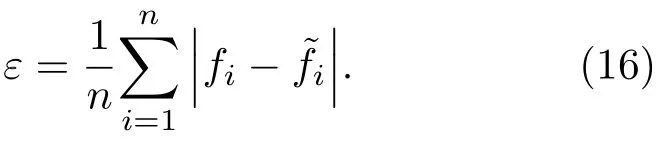
圖7 本文方法與傳統相干幾何法的平均誤差對比Fig.7 Comparison of average errors of the proposed method and the traditional coherent method

從圖7所示的結果來看，在各個測點處，本文方法相較于傳統相干幾何法均體現出了更高的精度，在30～1000 Hz范圍內，本文方法在所有測點處的平均誤差均小于2 Hz，而傳統相干幾何法則比本文方法平均誤差要高，進一步證明了本文方法的正確性。

為了進一步分析本文方法對空間聲場幅值分布預測的正確性，統計了不同方法在各個測點上的聲壓級分布對比，限于篇幅，此處給出了100 Hz、300 Hz、500 Hz、700 Hz等4個示例性頻率的對比圖，如圖8所示；另外以有限元法為標準參考方法，統計了本文方法以及傳統相干幾何法在各個測點上的聲壓級分布對比誤差，如圖9所示。

從圖8所示的測點聲壓級對比以及圖9所示的誤差對比來看，在100 Hz時，本文方法所得結果與有限元法比較接近，一方面是在各個測點的變化趨勢上具有良好的一致性，另一方面是在幅值上具有良好的一致性，而傳統幾何方法雖然在變化趨勢上較為接近，但是在幅值方面具有明顯的誤差，主要表現為在各個測點上的起伏性較低。這說明，在低頻處，真實聲場分布并不是均勻的，即擴散性較低。傳統的相干幾何法在模擬聲線跟蹤的過程中，受周期結構影響，在原本不會發生散射的位置模擬發生了聲線的散射，在一定程度上增加了聲場的擴散性，從而導致其精度較低，而本文方法則能夠準確模擬出散射的情況，從而具有較高的精度。當頻率升高時，聲場擴散性隨之升高，例如圖8(b)、圖8(c)、圖8(d)所示的300 Hz、500 Hz、700 Hz的情況，聲壓級的變化范圍趨向于減小，本文方法均達到了良好的仿真效果。當頻率較高時，傳統方法因為可以模擬聲場的這種擴散性，從而具有良好的模擬精度。除上述4個示例性頻率之外，從整個頻段的各個測點聲壓級分布來看，本文方法由于在低頻段能夠更加準確地模擬周期結構的散射規律，因此相較于傳統相干幾何法具有更高的精度，隨著頻率的升高，傳統方法對于周期結構散射現象的模擬逐漸適用，精度提高，同時本文方法仍具有較好的精度。

圖9 100 Hz、300 Hz、500 Hz、700 Hz時處各測點聲壓級分布誤差Fig.9 Errors of sound field distributions of the different methods at 100 Hz,300 Hz,500 Hz and 700 Hz

為了驗證本文方法在更加復雜的周期結構場景中的仿真精度，本文在上一個算例模型基礎上，在模型空間內部增加周期結構，如圖10所示。增加的周期結構處于與原周期結構相對的壁面上，新的周期結構L為0.1 m，高度H為0.1 m。本算例中，所有界面的聲阻抗仍設置為80ρ0c0。此算例中設置了一個點聲源，其位置為圖5(a)中橘色圓點所示的(2.4,0.2,0.2)m處，另外設置了1個測點，坐標為(0.6,1.8,0.3)m。經計算，有限元法、本文方法以及傳統相干幾何法在30～1000 Hz所得到的頻率響應如圖11所示。

圖10 算例2封閉空間及其網格劃分示意圖Fig.10 The schematic of room environment 2 and its mesh for FEM

圖11 測點處不同方法的頻率響應對比Fig.11 Comparison of frequency responses of different methods at the measuring point

圖11所示的頻響曲線對比表明，與算例1類似，本文方法在低頻段相較于傳統相干幾何法具有更高的精度，雖然本文方法與有限元法對比存在細微的頻率偏移，但是在頻率曲線的結構方面吻合度較高。在較高頻段，本文方法以及傳統相干幾何趨向于與有限元法結果一致，誤差均較低。此對比說明當空間內存在較為復雜的周期類型結構時，本文方法依然能夠給出良好的仿真結果。

3 結論

針對周期結構存在條件下的室內寬頻聲場仿真問題，本文發展了一種基于迭代散射模型的相干聲線跟蹤法。此方法在一定頻段范圍內將周期散射結構視為平面，然后基于周期散射定理，依據周期結構的輪廓尺寸以及聲波波長、入射角條件確定不同的散射波，此時原始聲線將會根據散射波情況迭代分裂為多個子聲線，此后繼續按照經典相干法對子聲線展開跟蹤，直到完成所有聲線的跟蹤。此迭代散射模型可準確模擬聲波在周期結構界面上的散射情況，相較于傳統的相干幾何法在低頻段有了較大的精度提高。此方法是對幾何聲學方法的有效補充，可為周期散射結構存在條件下的室內聲場仿真提供簡便且準確的新方法。