面向新工科的“誤差理論與數(shù)據(jù)處理”實(shí)踐平臺(tái)建設(shè)

劉蕓 王東 邢俊紅

[摘 要] 在新工科以培養(yǎng)多元化、創(chuàng)新型卓越工程人才背景下，“誤差理論與數(shù)據(jù)處理”課程實(shí)踐教學(xué)以提高學(xué)生創(chuàng)新能力及解決復(fù)雜工程問題為目標(biāo)，設(shè)計(jì)了一個(gè)從數(shù)據(jù)獲取、數(shù)據(jù)采集、數(shù)據(jù)處理到數(shù)據(jù)分析的全過程實(shí)踐實(shí)訓(xùn)，建立了一個(gè)集多個(gè)誤差處理功能于一體的實(shí)踐平臺(tái)，培養(yǎng)學(xué)生發(fā)現(xiàn)與解決問題、方案創(chuàng)新設(shè)計(jì)、個(gè)人分工與團(tuán)隊(duì)合作等能力。通過實(shí)踐全過程訓(xùn)練，強(qiáng)化學(xué)生理論聯(lián)系實(shí)際及實(shí)踐動(dòng)手能力，為后續(xù)不斷推進(jìn)課程改革奠定基礎(chǔ)。

[關(guān)鍵詞] 新工科;實(shí)踐課程改革;實(shí)踐平臺(tái)建設(shè);“誤差理論與數(shù)據(jù)處理”課程

[基金項(xiàng)目] 2018年度西安理工大學(xué)教育教學(xué)改革研究項(xiàng)目“面向新工科的‘誤差理論與數(shù)據(jù)處理’課程改革與實(shí)踐”（xjy1845）;2018年度西安理工大學(xué)教育教學(xué)改革研究項(xiàng)目“激光原理與技術(shù)精品資源共享課建設(shè)與實(shí)踐”（xjy1802）;2021年度西安理工大學(xué)省級(jí)大學(xué)生創(chuàng)新創(chuàng)業(yè)訓(xùn)練計(jì)劃項(xiàng)目“基于光學(xué)干涉原理的微球三維形貌測(cè)量技術(shù)研究”（S202110700096）

[作者簡介] 劉 蕓（1980—），女，黑龍江海倫人，工學(xué)博士，西安理工大學(xué)機(jī)械與精密儀器工程學(xué)院副教授，主要從事激光精密測(cè)量技術(shù)研究。

[中圖分類號(hào)] G642? ?[文獻(xiàn)標(biāo)識(shí)碼] A? ?[文章編號(hào)] 1674-9324（2021）47-0020-04? ? [收稿日期] 2021-09-30

一、引言

人類在進(jìn)行科學(xué)研究過程中，任何科學(xué)實(shí)驗(yàn)和工程實(shí)踐都離不開測(cè)量，沒有測(cè)量就沒有科學(xué)。由于測(cè)量中必然存在誤差，其會(huì)影響測(cè)量實(shí)驗(yàn)數(shù)據(jù)的準(zhǔn)確性，因此，科學(xué)實(shí)驗(yàn)和工程實(shí)踐獲得的數(shù)據(jù)信息必須經(jīng)過合理的數(shù)據(jù)處理，給出科學(xué)的評(píng)價(jià)，才有其實(shí)際價(jià)值。“誤差理論與數(shù)據(jù)處理”課程旨在使學(xué)生掌握機(jī)械量、幾何量和有關(guān)物理量測(cè)試技術(shù)中的誤差理論與數(shù)據(jù)處理方法，以培養(yǎng)學(xué)生具有對(duì)測(cè)量結(jié)果進(jìn)行處理、分析的能力，對(duì)保證精度要求條件下進(jìn)行測(cè)量方法和測(cè)量儀器的設(shè)計(jì)具有重要作用[1]。學(xué)生對(duì)“誤差理論與數(shù)據(jù)處理”課程知識(shí)的掌握程度，將對(duì)其今后從事的精密檢測(cè)、計(jì)量管理、質(zhì)量控制、儀器設(shè)計(jì)及制造等工作產(chǎn)生持續(xù)深遠(yuǎn)的影響。

在國家實(shí)施創(chuàng)新驅(qū)動(dòng)、“中國制造2025”“互聯(lián)網(wǎng)+”“一帶一路”等背景下，面對(duì)新技術(shù)、新業(yè)態(tài)、新產(chǎn)業(yè)、新模式，2017年以來，教育部積極推進(jìn)新工科建設(shè)，先后形成了“復(fù)旦共識(shí)”“天大行動(dòng)”和“北京指南”，主旨是以應(yīng)對(duì)變化、塑造未來為建設(shè)理念，以繼承與創(chuàng)新、交叉與融合、協(xié)調(diào)與共享為主要途徑，培養(yǎng)多元化、創(chuàng)新型卓越工程人才，為未來提供智力和人才支撐。因此，在新工科的大背景下，省級(jí)一流課程“誤差理論與數(shù)據(jù)處理”如何革新課程實(shí)踐，構(gòu)建以解決復(fù)雜工程問題為目標(biāo)的課程體系，已成為新工科建設(shè)的迫切需求[2]。

二、實(shí)踐教學(xué)改革

作為測(cè)控技術(shù)與儀器專業(yè)的一門專業(yè)課，“誤差理論與數(shù)據(jù)處理”課程以線性代數(shù)、概率論與數(shù)理統(tǒng)計(jì)課程為先修課程，與傳感器、測(cè)控電路、激光精密測(cè)量等專業(yè)課程緊密銜接，是一門理論性與實(shí)踐性較強(qiáng)的課程。目前，課程采用多媒體授課，線上與線下模式相結(jié)合，包括系統(tǒng)誤差、隨機(jī)誤差和粗大誤差的基本性質(zhì)與處理、誤差的合成與分配、測(cè)量不確定度、最小二乘法處理和回歸分析等幾個(gè)模塊，涉及的理論推導(dǎo)與經(jīng)典公式較多，對(duì)于知識(shí)點(diǎn)的鞏固多采用例題、堂測(cè)和習(xí)題的形式開展，學(xué)生對(duì)于實(shí)際測(cè)量中的誤差分析掌握不好，實(shí)踐能力得不到明顯提高，難以解決工程實(shí)際中的誤差分析及數(shù)據(jù)處理問題[3]。例如，最小二乘法處理在工程實(shí)踐中應(yīng)用非常廣泛，課堂練習(xí)多以兩個(gè)或三個(gè)待測(cè)最小二乘估計(jì)量為例進(jìn)行求解和分析，但當(dāng)待測(cè)估計(jì)量數(shù)目多于三個(gè)時(shí)，采用經(jīng)典的代數(shù)法或矩陣法計(jì)算，會(huì)發(fā)現(xiàn)計(jì)算過程煩瑣，數(shù)據(jù)處理量較大，學(xué)生往往感到棘手。將數(shù)據(jù)處理軟件Matlab或LabVIEW引入課堂，利用軟件強(qiáng)大的數(shù)據(jù)處理能力，不僅可以提高誤差數(shù)據(jù)處理的效率，而且能夠保證處理結(jié)果的準(zhǔn)確性和精確性[4，5]。目前，本課程已經(jīng)開設(shè)了關(guān)于Matlab數(shù)據(jù)處理實(shí)踐課程，包括等精度數(shù)據(jù)處理和最小二乘法數(shù)據(jù)處理內(nèi)容，但僅是各知識(shí)點(diǎn)的數(shù)據(jù)處理分析，相對(duì)獨(dú)立和分散，學(xué)生缺少動(dòng)手收集數(shù)據(jù)的過程以及實(shí)踐平臺(tái)的系統(tǒng)開發(fā)。因此，合理地設(shè)計(jì)實(shí)踐實(shí)訓(xùn)，開發(fā)相應(yīng)的教學(xué)實(shí)踐平臺(tái)，是課程實(shí)踐教學(xué)環(huán)節(jié)亟待解決的問題。

本專業(yè)“誤差理論與數(shù)據(jù)處理”課程實(shí)踐環(huán)節(jié)包括數(shù)據(jù)獲取和數(shù)據(jù)處理兩部分。數(shù)據(jù)獲取通過實(shí)驗(yàn)測(cè)量環(huán)節(jié)完成，數(shù)據(jù)處理則利用LabVIEW和Matlab相結(jié)合，建立一個(gè)集粗大誤差、系統(tǒng)誤差和隨機(jī)誤差計(jì)算、等精度與不等精度數(shù)據(jù)處理、最小二乘法及回歸分析等功能的實(shí)踐平臺(tái)，實(shí)現(xiàn)了從數(shù)據(jù)獲取到數(shù)據(jù)處理、分析的全過程實(shí)踐訓(xùn)練，提高學(xué)生學(xué)習(xí)該課程的興趣，使實(shí)踐教學(xué)真正成為培養(yǎng)學(xué)生創(chuàng)新實(shí)踐能力的重要環(huán)節(jié)。

（一）實(shí)驗(yàn)數(shù)據(jù)獲取

本課程開設(shè)了兩個(gè)典型測(cè)量實(shí)驗(yàn)，一個(gè)是綜合性實(shí)驗(yàn)，即利用萬能測(cè)長儀完成不同球體的直徑測(cè)量，學(xué)生通過操作萬能測(cè)長儀測(cè)量球體的不同弦長，利用不同測(cè)量方法獲得球體的直徑，使學(xué)生理解如何選擇測(cè)量中的最佳方案。另一個(gè)是驗(yàn)證性實(shí)驗(yàn)，通過阿貝比長儀實(shí)現(xiàn)對(duì)線紋尺的檢定，學(xué)生通過不同刻線長度的組合測(cè)量，掌握組合測(cè)量提高精度的方法。兩個(gè)實(shí)驗(yàn)都是以團(tuán)隊(duì)合作方式進(jìn)行，學(xué)生學(xué)會(huì)相應(yīng)儀器的使用方法，小組成員分工協(xié)作，共同完成實(shí)驗(yàn)設(shè)備的操作、數(shù)據(jù)的采集與記錄、數(shù)據(jù)的分析等。通過實(shí)驗(yàn)使學(xué)生能夠鞏固和加深理論課中所學(xué)的有關(guān)誤差分析和數(shù)據(jù)處理的基本知識(shí)，驗(yàn)證所學(xué)理論。

（二）實(shí)踐平臺(tái)建設(shè)

通過最佳測(cè)量方案比較和組合測(cè)量兩個(gè)實(shí)驗(yàn)，實(shí)現(xiàn)了測(cè)量數(shù)據(jù)的獲取，分別利用誤差實(shí)踐平臺(tái)的等精度數(shù)據(jù)處理模塊和最小二乘法模塊，完成了數(shù)據(jù)的自動(dòng)分析及處理，實(shí)現(xiàn)了球體的直徑測(cè)量和線紋尺的標(biāo)定。要求學(xué)生對(duì)相關(guān)軟件達(dá)到初步掌握，能夠根據(jù)具體測(cè)量數(shù)據(jù)，設(shè)計(jì)程序并編程調(diào)試，記錄和分析數(shù)據(jù)結(jié)果。

在實(shí)驗(yàn)教學(xué)中，通過小組方案競(jìng)爭、現(xiàn)場(chǎng)操作、程序設(shè)計(jì)、實(shí)驗(yàn)報(bào)告等考核手段，評(píng)價(jià)學(xué)生能力的達(dá)成效果，以實(shí)現(xiàn)實(shí)驗(yàn)教學(xué)目標(biāo)。通過這一系列的實(shí)踐實(shí)訓(xùn)，培養(yǎng)學(xué)生發(fā)現(xiàn)與解決問題、創(chuàng)新設(shè)計(jì)方案、個(gè)人分工與團(tuán)隊(duì)合作等能力，通過實(shí)驗(yàn)全過程訓(xùn)練強(qiáng)化學(xué)生理論聯(lián)系實(shí)際及實(shí)踐動(dòng)手能力。

三、實(shí)踐平臺(tái)設(shè)計(jì)

本課程實(shí)踐平臺(tái)將LabVIEW和Matlab軟件相結(jié)合，利用LabVIEW軟件的可視化及Matlab強(qiáng)大的數(shù)據(jù)處理能力，實(shí)現(xiàn)數(shù)據(jù)的采集、處理和分析功能。首先，設(shè)計(jì)了等精度與不等精度數(shù)據(jù)處理模塊，包括發(fā)現(xiàn)并剔除粗大誤差、判斷系統(tǒng)誤差以及隨機(jī)誤差的計(jì)算功能;其次，完成了等精度與不等精度最小二乘法求解最可信賴值及其精度的數(shù)據(jù)處理模塊;最后，設(shè)計(jì)了一元線性回歸分析模塊，實(shí)現(xiàn)了測(cè)量數(shù)據(jù)的線性擬合和回歸方程的統(tǒng)計(jì)檢驗(yàn)。以實(shí)驗(yàn)獲取的測(cè)量數(shù)據(jù)為對(duì)象，對(duì)實(shí)踐平臺(tái)的各個(gè)功能模塊進(jìn)行了驗(yàn)證。該課程實(shí)踐平臺(tái)具有人機(jī)交互友好、可靠性高、操作簡單等優(yōu)點(diǎn)。

（一）平臺(tái)界面設(shè)計(jì)

課程實(shí)踐平臺(tái)界面利用LabVIEW軟件開發(fā)，界面一共有四個(gè)選項(xiàng)，分別是“不等精度”“等精度”“最小二乘法”和“回歸分析”。學(xué)生可以根據(jù)數(shù)據(jù)處理需求自行選擇進(jìn)入，界面如圖1所示。

（二）等精度與不等精度數(shù)據(jù)處理模塊設(shè)計(jì)

以等精度數(shù)據(jù)處理為例，點(diǎn)擊輸入控件，測(cè)量數(shù)據(jù)以Excel表格形式導(dǎo)入系統(tǒng)，點(diǎn)擊“剔除粗大誤差”按鈕，學(xué)生可以選擇3σ準(zhǔn)則或者格羅布斯準(zhǔn)則進(jìn)行粗大誤差判斷，并將含有粗大誤差的測(cè)量數(shù)據(jù)剔除，生成新的Excel表格。點(diǎn)擊“判斷系統(tǒng)誤差”按鈕，選擇馬利科夫準(zhǔn)則或不同公式計(jì)算標(biāo)準(zhǔn)差比較法判斷同組間測(cè)量數(shù)據(jù)是否含有系統(tǒng)誤差。點(diǎn)擊“開始計(jì)算”，系統(tǒng)運(yùn)行Matlab程序，計(jì)算出測(cè)量列的算術(shù)平均值、標(biāo)準(zhǔn)差、算術(shù)平均值的標(biāo)準(zhǔn)差以及極限誤差，結(jié)果如圖2所示。該模塊完成了粗大誤差剔除、系統(tǒng)誤差判斷和隨機(jī)誤差計(jì)算的功能，可以實(shí)現(xiàn)等精度測(cè)量數(shù)據(jù)列或不等精度測(cè)量數(shù)據(jù)列的數(shù)據(jù)處理及分析。

（三）最小二乘法和一元回歸數(shù)據(jù)處理模塊設(shè)計(jì)

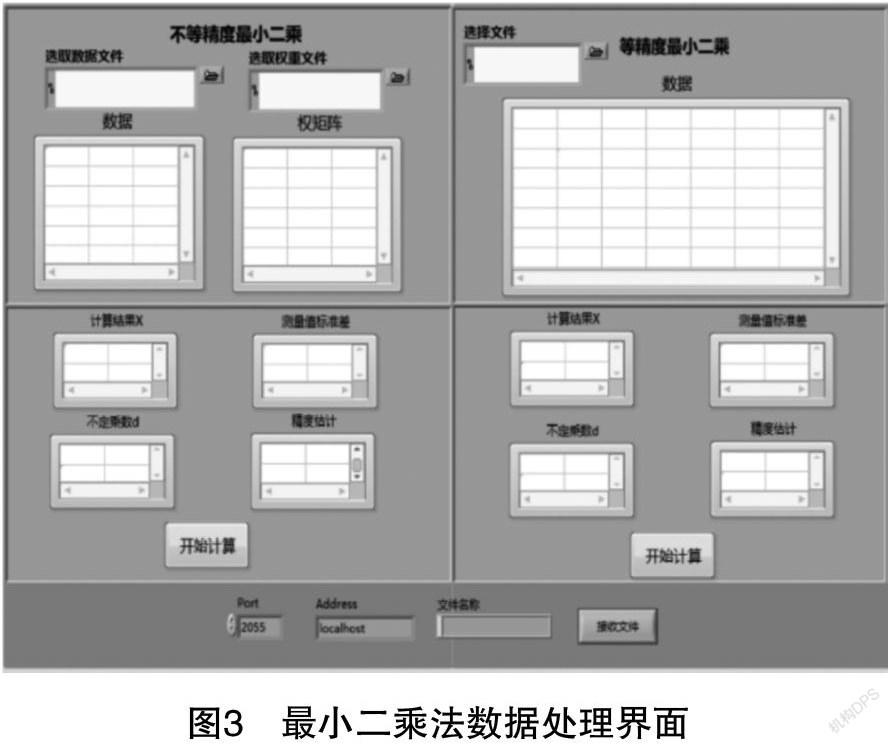
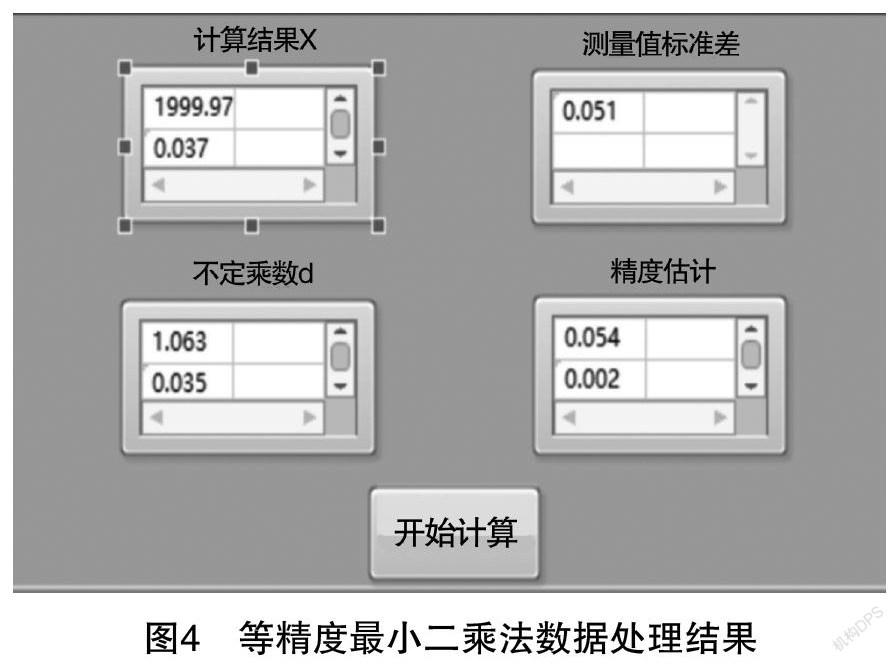
最小二乘界面包括“等精度最小二乘”和“不等精度最小二乘”兩個(gè)數(shù)據(jù)處理模式，如圖3所示。以等精度最小二乘為例，輸入阿貝比長儀測(cè)量線紋尺的各組數(shù)據(jù)后，點(diǎn)擊“開始計(jì)算”按鈕，程序會(huì)調(diào)用Matlab編寫的程序依次計(jì)算出“計(jì)算結(jié)果X”“測(cè)量值標(biāo)準(zhǔn)差”“不定乘數(shù)”和“精度估計(jì)”的結(jié)果，如圖4所示。利用Matlab軟件通過矩陣法可以計(jì)算出多個(gè)待測(cè)參數(shù)的估計(jì)量，并對(duì)其進(jìn)行精度估計(jì)，解決了手動(dòng)計(jì)算煩瑣的問題。一元回歸分析功能，點(diǎn)擊相應(yīng)控件，系統(tǒng)會(huì)自動(dòng)運(yùn)行程序，求解出待求一元回歸參數(shù)、回歸平方和、殘余平方和，并對(duì)該方程進(jìn)行F顯著性檢驗(yàn)，以檢驗(yàn)線性擬合方程的效果。這兩個(gè)數(shù)據(jù)處理功能的實(shí)現(xiàn)，都需要學(xué)生自己編程調(diào)試，掌握軟件編程方法，以提高學(xué)生分析問題和解決問題的能力。

（四）TCP通信程序設(shè)計(jì)

LabVIEW軟件可以實(shí)現(xiàn)網(wǎng)絡(luò)數(shù)據(jù)傳輸，在服務(wù)端編寫對(duì)DAQ設(shè)備進(jìn)行控制的程序，采集測(cè)量數(shù)據(jù)，在TCP節(jié)點(diǎn)調(diào)控下在網(wǎng)上發(fā)布數(shù)據(jù)，通過TCP節(jié)點(diǎn)，客戶端接收數(shù)據(jù)，完成遠(yuǎn)程數(shù)據(jù)采集。在初始化后，服務(wù)端與客戶端之間建立聯(lián)系，由服務(wù)端接收到的數(shù)據(jù)經(jīng)過操作被客戶端接收，數(shù)據(jù)會(huì)被導(dǎo)入到Excel文件中。通過設(shè)計(jì)TCP通信程序，可實(shí)現(xiàn)服務(wù)端與客戶端之間的交互性功能。

四、總結(jié)

新工科的一項(xiàng)共識(shí)是加強(qiáng)研究和實(shí)踐，培養(yǎng)造就一批多樣化、創(chuàng)新型卓越工程科技人才，而課程實(shí)踐教學(xué)就是在校生提高創(chuàng)新和實(shí)踐能力的一個(gè)重要途徑。“誤差理論與數(shù)據(jù)處理”課程實(shí)踐教學(xué)設(shè)計(jì)了一套包括數(shù)據(jù)獲取、數(shù)據(jù)采集、數(shù)據(jù)處理、數(shù)據(jù)分析功能的實(shí)踐實(shí)訓(xùn)，建立了一個(gè)集等精度與不等精度數(shù)據(jù)處理模塊、等精度與不等精度最小二乘法處理模塊、一元線性回歸分析模塊等多個(gè)誤差處理功能于一體的實(shí)踐平臺(tái)，提高了學(xué)生利用專業(yè)知識(shí)解決復(fù)雜工程實(shí)踐問題的能力。后續(xù)需繼續(xù)豐富實(shí)踐內(nèi)容，持續(xù)提升教學(xué)質(zhì)量，不斷推進(jìn)課程改革。

參考文獻(xiàn)

[1]劉蕓，趙敏，焦明星，等.工程教育專業(yè)認(rèn)證背景下“誤差理論與數(shù)據(jù)處理”課程教學(xué)改革[J].教育教學(xué)論壇，2018（49）：124-126.

[2]王飛，劉繼承，陳飛，等.新工科背景下誤差理論與數(shù)據(jù)處理課程的改革與實(shí)驗(yàn)探究[J].中國現(xiàn)代教育裝備，2019（17）：102-104+108.

[3]宋哲英，宋雪玲.基于OBE的工程教育模式下“誤差理論與數(shù)據(jù)處理”課程改革[J].高教學(xué)刊，2016（16）：153-154+156.

[4]蔣彥，朱慧玲，謝靜，等.LabVIEW在誤差理論與數(shù)據(jù)處理實(shí)驗(yàn)中的應(yīng)用[J].高師理科學(xué)刊，2016，36（2）：87-89.

[5]萬文.虛擬儀器在評(píng)定直線度誤差實(shí)驗(yàn)教學(xué)中的應(yīng)用[J].實(shí)驗(yàn)室研究與探索，2018，37（11）：121-124.