諧波齒輪傳動(dòng)柔輪的應(yīng)力和疲勞強(qiáng)度分析*

王玉玲 張旭剛 張 華 江志剛

(①武漢科技大學(xué)冶金裝備及其控制教育部重點(diǎn)實(shí)驗(yàn)室，湖北 武漢430081；②武漢科技大學(xué)機(jī)械傳動(dòng)與制造工程湖北省重點(diǎn)實(shí)驗(yàn)室，湖北 武漢430081)

諧波減速機(jī)是一種高精密減速傳動(dòng)裝置，由剛輪，柔輪和波發(fā)生器3個(gè)主要元件組成。它通過(guò)柔輪周期性的彈性變形和剛輪與柔輪的齒間嚙合來(lái)傳遞運(yùn)動(dòng)和動(dòng)力，具有體積小、傳動(dòng)比大和傳動(dòng)平穩(wěn)等優(yōu)點(diǎn)。柔輪作為諧波減速機(jī)的核心元件，其強(qiáng)度和壽命直接影響了整個(gè)諧波傳動(dòng)的可靠性和耐久性[1]。在交變載荷作用下，柔輪極易發(fā)生疲勞斷裂[2]，嚴(yán)重影響了諧波傳動(dòng)的精度和效率。因此，對(duì)柔輪的應(yīng)力和疲勞強(qiáng)度分析有助于提高諧波減速機(jī)工作性能和使用壽命

隨著計(jì)算機(jī)性能的提升和有限元方法的發(fā)展，有了許多關(guān)于柔輪應(yīng)力和疲勞強(qiáng)度的研究。文獻(xiàn)[3]將柔輪輪齒簡(jiǎn)化為當(dāng)量齒圈，利用有限元方法研究柔輪壁厚、筒長(zhǎng)和齒寬對(duì)柔輪最大應(yīng)力的影響。文獻(xiàn)[4]建立了農(nóng)業(yè)機(jī)器人轉(zhuǎn)向機(jī)構(gòu)的杯形柔輪有限元模型，并結(jié)合理論分析了柔輪空載下的應(yīng)力分布狀況。文獻(xiàn)[5]建立了柔輪的實(shí)體模型并導(dǎo)入到ANSYS軟件中對(duì)其進(jìn)行壽命仿真和評(píng)估，沒(méi)有給出柔輪疲勞強(qiáng)度的理論分析。以往關(guān)于柔輪有限元分析的研究，很少采用理論計(jì)算與仿真相結(jié)合的方法，也很少分析柔輪在不同負(fù)載下應(yīng)力和疲勞安全系數(shù)分布規(guī)律。因此本文在Inventor中建立了未簡(jiǎn)化輪齒的杯型柔輪模型，以提高有限元的仿真精度。對(duì)柔輪有限元模型進(jìn)行結(jié)構(gòu)靜力仿真，并結(jié)合理論計(jì)算，得到了柔輪負(fù)載下應(yīng)力和位移的變化規(guī)律，在此基礎(chǔ)上研究了柔輪負(fù)載時(shí)疲勞壽命，該結(jié)論對(duì)提高諧波減速機(jī)柔輪的工作壽命具有一定的參考價(jià)值。

1 柔輪應(yīng)力分析

1.1 空載狀態(tài)下柔輪應(yīng)力分析

空載狀態(tài)下柔輪的應(yīng)力為預(yù)應(yīng)力，是在裝配時(shí)由于橢圓凸輪波發(fā)生器的作用而使柔輪變形時(shí)產(chǎn)生的[6]。這個(gè)變形力可以通過(guò)分析橢圓凸輪模型在長(zhǎng)軸方向?qū)θ彷啴a(chǎn)生的徑向變形量來(lái)確定。本文根據(jù)文獻(xiàn)[7]的柔輪計(jì)算模型，采用四力作用式凸輪波發(fā)生器，如圖1所示。

由圓柱殼體理論有，柔輪在該波發(fā)生器作用下的徑向變形為：

w=w0cos(2φ)

(1)

柔輪空載下沿軸線方向的彎曲應(yīng)力為：

(2)

柔輪空載下沿周向彎曲應(yīng)力為：

(3)

柔輪空載下扭轉(zhuǎn)剪應(yīng)力為：

(4)

式中：w0為柔輪最大徑向變形量；s1為柔輪齒圈處壁厚；w為柔輪徑向變形量；L為柔輪筒體長(zhǎng)度；φ為以長(zhǎng)軸為計(jì)算起點(diǎn)度量的角度；rm為輪中線的半徑；E為彈性模量；v為泊松比。

本文以某型號(hào)諧波減速機(jī)為研究對(duì)象，其剛輪、柔輪、柔性軸承和波發(fā)生器的裝配圖如圖2所示，柔輪相關(guān)參數(shù)為w0=0.372 mm,s1=1.376 mm,L=34 mm,rm=31.35 mm, 柔輪的材料選用40CrNiMoA,其彈性模量和泊松比分別為209 GPa和0.3。將柔輪的結(jié)構(gòu)參數(shù)代入上述幾個(gè)式子，可以解出柔輪空載下的最大應(yīng)力值為166.98 MPa。

1.2 空載下柔輪應(yīng)力有限元分析和驗(yàn)證

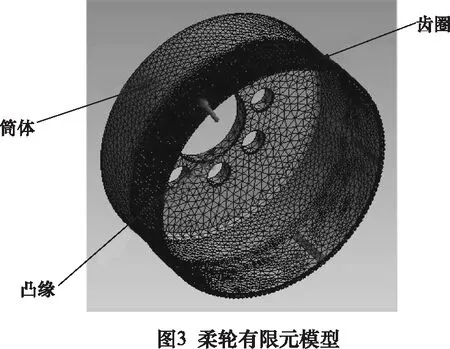
首先在Inventor軟件中建立柔輪的三維模型，然后將其導(dǎo)人到ANSYS Workbench中。為了便于網(wǎng)格的劃分和載荷的添加，將柔輪切分為4部分，分別是齒圈、筒體、筒體與凸緣過(guò)渡部分和筒體凸緣部分。在柔輪齒圈內(nèi)側(cè)劃分出4個(gè)小矩形區(qū)域來(lái)施加相應(yīng)壓力。由于所選型號(hào)的諧波減速機(jī)中柔輪與箱體是靠螺栓連接的，因此將柔輪底部8個(gè)小圓柱面施加固定約束。柔輪有限元模型如圖3所示。

對(duì)柔輪進(jìn)行靜力結(jié)構(gòu)分析，得到柔輪的等效應(yīng)力和位移云圖如圖4所示。從柔輪等效應(yīng)力云圖上可以看到柔輪受到波發(fā)生器的最大應(yīng)力主要集中在齒圈中部(波發(fā)生器長(zhǎng)軸作用區(qū)域)以及齒圈和筒體的過(guò)渡區(qū)域，且最大應(yīng)力值為165.09 MPa，考慮到施加壓力的過(guò)程中會(huì)造成一定的應(yīng)力集中，所以去掉這個(gè)最大值，觀察齒圈中部的應(yīng)力主要集中在140～165 MPa，這與之前理論計(jì)算得到的166.98 MPa相比，誤差不是很大，說(shuō)明柔輪應(yīng)力的仿真結(jié)果符合實(shí)際情況。從柔輪的變形云圖中可以看到柔輪最大變形量為0.373 96 mm，而此型號(hào)的柔輪徑向最大變形0.372 mm。

1.3 負(fù)載下柔輪應(yīng)力和變形規(guī)律

為了得到柔輪疲勞強(qiáng)度與負(fù)載的關(guān)系以及確定柔輪的工作負(fù)荷，本文研究了柔輪在不同扭矩作用下的應(yīng)力和位移變化情況。柔輪在負(fù)載時(shí)與剛輪嚙合，主要受到凸輪對(duì)柔輪的變形力和剛輪輪齒產(chǎn)生的扭矩。柔輪負(fù)載下的邊界約束與空載狀態(tài)下有一定的不同。本文采用文獻(xiàn)[8]的方法，在波發(fā)生器長(zhǎng)軸方向上的兩個(gè)相對(duì)應(yīng)輪齒節(jié)圓上的若干節(jié)點(diǎn)上施加切向力以模擬柔輪輪齒所受到剛輪輪齒產(chǎn)生的扭矩，切向力與所施加扭矩有以下關(guān)系：

(5)

式中：M為施加的扭矩，R為柔輪的節(jié)圓半徑，N為柔輪輪齒節(jié)圓上所施加切向力的節(jié)點(diǎn)數(shù)。

本文N=11，選取7組不同的扭矩值。由式(5)，扭矩值和施加的切向力的數(shù)值如表1所示。

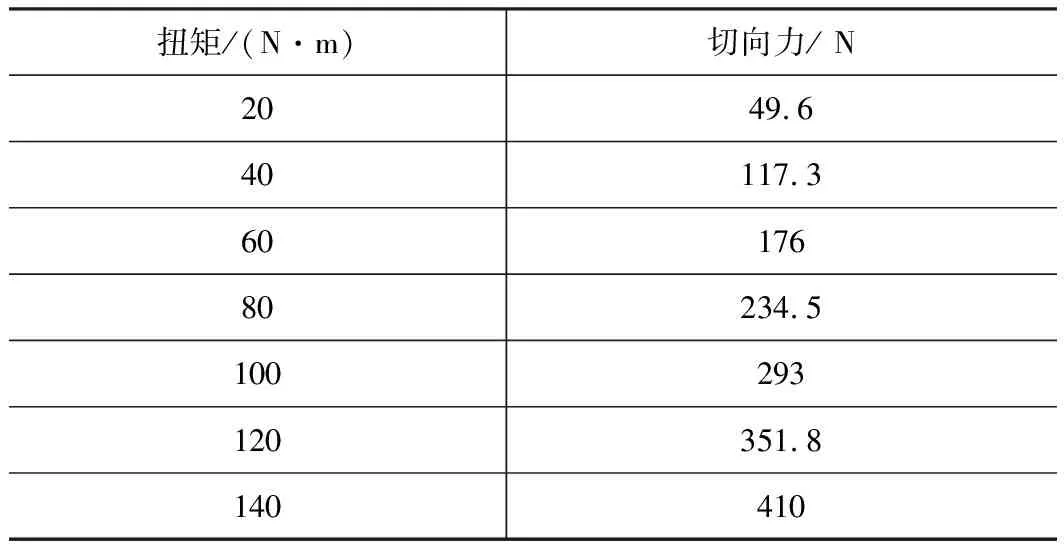
表1 柔輪輪齒上的載荷換算

當(dāng)柔輪受到負(fù)載時(shí),對(duì)其進(jìn)行靜力結(jié)構(gòu)分析，可以得到不同扭矩下柔輪的應(yīng)力和變形云圖。圖5顯示了T=60 N·m作用下的有限元分析云圖。

從圖中可以看到，柔輪應(yīng)力和變形云圖形狀并沒(méi)有發(fā)生較大的改變，但是柔輪的最大等效應(yīng)力和最大變形量都增加了，此外筒體和凸緣的連接部分也出現(xiàn)了一定的應(yīng)力集中。為了更清晰地呈現(xiàn)柔輪最大等效應(yīng)力和位移隨負(fù)載分布狀況，將7種扭矩作用下的柔輪最大等效應(yīng)力云圖和柔輪在齒圈和筒體過(guò)渡處(即軸向長(zhǎng)度x=13.67 mm)的變形云圖分別繪制成曲線圖，如圖6所示。

圖6a顯示，隨著扭矩的增大，柔輪最大等效應(yīng)力值也在不斷增大，在空載到負(fù)載100 N·m的時(shí)候，應(yīng)力的增值比較平穩(wěn)，而在100 N·m 之后，最大應(yīng)力值快速增長(zhǎng)。因此對(duì)于柔輪材料為40CrNiMoA，模數(shù)是0.39 mm，筒體壁厚為0.6 mm的柔輪在100 N·m以下為最佳工作載荷段。

圖6b顯示，柔輪的最大變形是呈諧波形狀的，且為對(duì)稱分布，柔輪的最大位移出現(xiàn)在周向長(zhǎng)度為30 mm、80 mm、130 mm和180 mm附近，分別對(duì)應(yīng)著柔輪長(zhǎng)軸即凸輪波發(fā)生器作用位置和柔輪短軸處。其次在柔輪受到的扭矩較小時(shí)即T=20 N·m時(shí)，其變形曲線與扭矩較大時(shí)相比偏移了一個(gè)相位角。隨著扭矩的逐漸增大，柔輪最大位移值每次只增長(zhǎng)大約0.1 mm，柔輪筒體變形云圖的顏色分布沒(méi)有發(fā)生明顯的改變，說(shuō)明負(fù)載的變化對(duì)柔輪變形規(guī)律沒(méi)有太大影響，柔輪最大徑向變形取決于波發(fā)生器的輪廓形狀。

2 柔輪疲勞分析

2.1 柔輪疲勞強(qiáng)度理論

柔輪是諧波減速機(jī)中最關(guān)鍵也是最易受損的零件，在交變載荷下，柔輪易發(fā)生疲勞斷裂。因此柔輪的疲勞強(qiáng)度分析對(duì)提高諧波減速機(jī)的傳動(dòng)精度具有重要的意義。本文先采用理論計(jì)算的方法求出柔輪在負(fù)載T=100 N·m時(shí)的安全因子，然后再對(duì)其進(jìn)行疲勞壽命的有限元仿真以驗(yàn)證理論結(jié)果的可靠性。

柔輪沿軸線方向的正應(yīng)力、周向正應(yīng)力和變形產(chǎn)生的剪應(yīng)力分別為[5]：

(6)

(7)

(8)

令扭矩為T(mén)，則作用于柔輪上的切應(yīng)力為：

(9)

采用雙向穩(wěn)定變應(yīng)力狀態(tài)下的安全系數(shù)來(lái)校驗(yàn)柔輪的疲勞強(qiáng)度。

只有切應(yīng)力作用時(shí)柔輪的安全系數(shù)為：

(10)

只有正應(yīng)力作用時(shí)柔輪的安全系數(shù)為：

(11)

正應(yīng)力和切應(yīng)力同時(shí)作用時(shí)的柔輪疲勞安全系數(shù)可以表示為：

(12)

表2 Cσ、C與β的取值

因?yàn)槿彷喌钠诎踩禂?shù)不應(yīng)小于1.5，上式計(jì)算的柔輪在負(fù)載T=100 N·m時(shí)的安全系數(shù)是1.607>1.5,說(shuō)明柔輪符合疲勞強(qiáng)度要求。

2.2 柔輪疲勞有限元分析

為了驗(yàn)證柔輪在負(fù)載T=100 N·m時(shí)疲勞強(qiáng)度計(jì)算結(jié)果的可靠性，在有限元軟件中插入疲勞工具，輸入柔輪材料的S-N曲線即交變應(yīng)力幅值與工作循環(huán)次數(shù)曲線。設(shè)置載荷類型為Fully Reversed，最終可得到柔輪在扭矩T=100 N·m下的疲勞壽命云圖和安全系數(shù)云圖，如圖7所示。柔輪在此工作狀態(tài)下疲勞壽命為106次，最小疲勞安全因子為1.615 4，主要位置是柔輪齒圈、柔輪齒圈與筒體過(guò)渡處和筒體與凸緣過(guò)渡處，與理論計(jì)算值1.607的誤差為0.46%，說(shuō)明理論計(jì)算的結(jié)果可靠。

將柔輪在不同負(fù)載下的安全系數(shù)繪制成曲線如圖8所示，可知在扭矩T≥110 N·m時(shí)柔輪易發(fā)生疲勞失效。

3 結(jié)語(yǔ)

本文利用Inventor軟件和ANSYS Workbench仿真軟件對(duì)諧波減速機(jī)的柔輪進(jìn)行了應(yīng)力和疲勞分析，并結(jié)合圓柱殼體理論和疲勞強(qiáng)度理論驗(yàn)證了分析結(jié)果的可靠性。通過(guò)分析柔輪在空載和負(fù)載狀態(tài)下的應(yīng)力和變形規(guī)律，得到如下結(jié)論：

(1)柔輪最大變形量集中在柔輪長(zhǎng)軸和短軸區(qū)域，在負(fù)載較小時(shí)，此變形規(guī)律會(huì)偏移一個(gè)相位角。

(2) 柔輪最大等效應(yīng)力集中在齒圈位置，齒圈與筒體過(guò)渡位置和凸緣與筒體的過(guò)渡位置。

(3)扭矩的增大對(duì)柔輪最大位移影響不大，柔輪的最大徑向位移是由凸輪波發(fā)生器決定的，而最大應(yīng)力值隨著負(fù)載的增大而增大，且柔輪的最佳工作載荷范圍是T≤100 N·m。

(4)柔輪的疲勞系數(shù)隨負(fù)載的增大而迅速降低，在扭矩T=110 N·m左右時(shí)，柔輪易發(fā)生疲勞斷裂。該研究方法和結(jié)論能為柔輪結(jié)構(gòu)設(shè)計(jì)，應(yīng)力分析和疲勞優(yōu)化提供一定的理論和技術(shù)支持。