基于條件深度循環(huán)生成對抗網(wǎng)絡(luò)和動作探索的行星輪軸承剩余壽命預(yù)測

于軍， 劉可， 郭帥， 于廣濱， 郭振宇

(1.哈爾濱理工大學(xué) 先進制造智能化技術(shù)教育部重點實驗室, 黑龍江 哈爾濱 150080；2.礦冶過程自動控制技術(shù)國家重點實驗室， 北京 100089；3.哈爾濱理工大學(xué) 自動化學(xué)院， 黑龍江 哈爾濱 150080；4.中國船舶重工集團公司第703研究所 蒸汽輪機事業(yè)部， 黑龍江 哈爾濱 150078)

0 引言

因具有傳動比大和結(jié)構(gòu)緊湊等特點，行星齒輪箱已廣泛應(yīng)用于直升機、風力發(fā)電機和坦克車等機械設(shè)備中[1-2]。復(fù)雜惡劣的工作環(huán)境會增加行星輪軸承故障的風險[3]。這種難以預(yù)料的故障可能導(dǎo)致整個設(shè)備突然失靈，甚至造成巨大的經(jīng)濟損失。因此，行星輪軸承剩余壽命預(yù)測對保障機械設(shè)備可靠運行和避免事故發(fā)生具有十分重要的意義。

近年來，國內(nèi)外學(xué)者對典型旋轉(zhuǎn)機械的剩余壽命預(yù)測問題進行了深入研究[4]，并提出了一些頗具代表性的軸承剩余壽命預(yù)測方法。這些方法主要分為3類：物理模型法、統(tǒng)計模型法和人工智能法。

物理模型法通過建立基于失效機理的數(shù)學(xué)模型，描述機械設(shè)備的退化過程。與材料特性相關(guān)的模型參數(shù)可通過專門的實驗或有限元分析方法獲得。典型的數(shù)學(xué)模型包括有限元模型、Paris模型[5]、動力學(xué)模型等。物理模型法雖然能實現(xiàn)軸承剩余壽命的準確預(yù)測，但在模型建立過程中需滿足多種假設(shè)，難以建立精確的剩余壽命預(yù)測模型。而且模型參數(shù)的確定依賴人工經(jīng)驗，從而限制了物理模型法的廣泛應(yīng)用。

統(tǒng)計模型法根據(jù)基于經(jīng)驗知識的統(tǒng)計學(xué)模型預(yù)測機械設(shè)備的剩余壽命。統(tǒng)計模型中的隨機變量常用于描述各種變化源的不確定性，因此，統(tǒng)計模型法能有效描述退化過程的不確定性并準確估計機械設(shè)備的剩余壽命。常用的統(tǒng)計模型包括自適應(yīng)回歸模型[6]、隨機系數(shù)模型[7]、Wiener過程模型[8]、全階乘模型[9]等。隨機變量的引入明顯提高了用于描述各種退化過程的模型柔性。然而，統(tǒng)計模型法的不足在于預(yù)測效果嚴重依賴歷史數(shù)據(jù)，導(dǎo)致剩余壽命預(yù)測得不準確。另外，隨機變量的概率分布需滿足多種假設(shè)，從而限制了統(tǒng)計模型法的實際應(yīng)用。

人工智能法通過智能技術(shù)識別機械設(shè)備的退化狀態(tài)，而非構(gòu)建物理模型或統(tǒng)計學(xué)模型。人工智能法能解決難于構(gòu)建物理模型或統(tǒng)計學(xué)模型的復(fù)雜機械系統(tǒng)剩余壽命預(yù)測問題。因此，人工智能法在軸承的剩余壽命預(yù)測領(lǐng)域受到極大關(guān)注。典型的人工智能法包括人工神經(jīng)網(wǎng)絡(luò)[10]、模糊邏輯系統(tǒng)、支持向量機(SVM)[11]、Gaussian過程回歸[12]等。人工智能法無需額外的先驗知識或精確的解析模型，通過歷史數(shù)據(jù)識別退化過程。因此，人工智能法在復(fù)雜系統(tǒng)的剩余壽命預(yù)測中具有重要的應(yīng)用價值。

行星輪軸承不但自轉(zhuǎn)，還繞太陽輪公轉(zhuǎn)。其內(nèi)圈安裝在行星輪軸上，相對于行星輪軸固定不動；外圈安裝在行星架上，隨著行星架的旋轉(zhuǎn)而旋轉(zhuǎn)。從故障位置到傳感器的時變振動傳遞路徑，使采集到的行星輪軸承振動信號具有非靜態(tài)的特點。此外，由于受到轉(zhuǎn)速和負載變化的影響，行星齒輪箱在變工況條件下運行，所采集到的振動信號往往是非線性的。行星輪軸承的疲勞壽命試驗耗時且投入巨大，僅能獲得有限的行星輪軸承全壽命周期樣本。行星輪軸承的剩余壽命預(yù)測需要大量訓(xùn)練樣本，導(dǎo)致行星輪軸承的剩余壽命預(yù)測模型無法得到充分訓(xùn)練。因此，小樣本和變工況下行星輪軸承的剩余壽命預(yù)測準確率較低。

本文將門控循環(huán)單元神經(jīng)網(wǎng)絡(luò)(GRUNN)與條件生成對抗網(wǎng)絡(luò)(CGAN)相結(jié)合，構(gòu)建一種深度學(xué)習(xí)模型，使該深度學(xué)習(xí)模型具有較強的非靜態(tài)和非線性信號處理能力，并能解決小樣本情況下行星輪軸承的剩余壽命預(yù)測問題，同時利用動作探索(AD)技術(shù)改善學(xué)習(xí)決策質(zhì)量、減少迭代次數(shù)。

1 理論基礎(chǔ)

1.1 門控循環(huán)單元神經(jīng)網(wǎng)絡(luò)

循環(huán)神經(jīng)網(wǎng)絡(luò)(RNN)通過建立單元間的循環(huán)連接，記憶任意長度序列的輸入數(shù)據(jù)[13]。RNN的關(guān)鍵在于t時刻輸出ht是由當前輸入xt和前一時刻輸出ht-1決定的。計算公式為

(1)

式中：W″和H為轉(zhuǎn)換矩陣；b″為偏置向量；f為非線性激活函數(shù)。

然而，常規(guī)RNN的訓(xùn)練過程可能導(dǎo)致梯度消失或梯度爆炸。為緩解這一問題，Chung等[14]開發(fā)了一種可實現(xiàn)狀態(tài)記憶和信息獲取的門控循環(huán)單元(GRU)，用于構(gòu)成GRUNN. GRU的結(jié)構(gòu)如圖1所示。重置門r用于調(diào)整新輸入與之前記憶的合并，更新門z用于調(diào)控之前記憶中保留的信息。GRU中的轉(zhuǎn)換函數(shù)定義如下：

zt=σ(Wzxt+Vzht-1+bz),

(2)

rt=σ(Wrxt+Vrht-1+br),

(3)

(4)

(5)

圖1 GRU的結(jié)構(gòu)Fig.1 Architecture of GRU

1.2 條件生成對抗網(wǎng)絡(luò)

生成對抗網(wǎng)絡(luò)(GAN)是2014年由Goodfellow等[15]提出的一種生成式模型，一經(jīng)提出就成為人工智能領(lǐng)域的研究熱點之一。GAN并不是一個完整的網(wǎng)絡(luò)模型，而是一種網(wǎng)絡(luò)訓(xùn)練框架。該框架僅有兩個組成部分：生成器和判別器。GAN的核心思想來源于博弈論中的零和博弈，將生成器和判別器看作博弈雙方。生成器用于生成盡量服從真實數(shù)據(jù)分布的樣本，判別器用于判斷輸入樣本是真實樣本還是生成樣本。優(yōu)化目標是通過對抗機制達到納什均衡。

CGAN是在GAN基礎(chǔ)上加入了額外的條件c(如類標簽)，通過額外的條件c指導(dǎo)數(shù)據(jù)的生成過程[16]。CGAN的模型結(jié)構(gòu)如圖2所示。輸入隨機噪聲n的同時輸入相應(yīng)條件c，使生成器G生成盡量服從真實數(shù)據(jù)分布Pdata(x)的樣本G(c,n)；在條件c的指導(dǎo)下，判別器D判斷輸入樣本是真實數(shù)據(jù)x還是生成樣本G(c,n)。目標函數(shù)V(D,G)為

En～Pn(n)[lg(1-D(G(n|c)))]，

(6)

式中：Pn(n)表示先驗噪聲分布；Ex～Pdata(x)[lgD(x|c)]表示將真實數(shù)據(jù)x與條件c輸入判別器D獲得是否為真實數(shù)據(jù)的概率；En～Pn(n)[lg(1-D(G(n|c)))]表示隨機噪聲n與條件c輸入生成器G產(chǎn)生的生成樣本，判別器D判別其為真實數(shù)據(jù)的概率。生成器G嘗試最小化目標函數(shù)，判別器D嘗試最大化目標函數(shù)。

圖2 CGAN的模型結(jié)構(gòu)Fig.2 Model structure of CGAN

1.3 動作探索

作為一種重要的機器學(xué)習(xí)方法，強化學(xué)習(xí)(RL)已廣泛應(yīng)用于控制工程、故障診斷和圖像處理等領(lǐng)域。它采用 “嘗試與失敗”機制，使智能體在與環(huán)境的交流中學(xué)習(xí)，利用評價性的反饋信號實現(xiàn)決策的優(yōu)化[17]。RL可用于解決智能體如何學(xué)習(xí)近似最優(yōu)行為策略的問題。RL的過程是一個試探與評價的過程，其基本框架如圖3所示。當環(huán)境狀態(tài)為st時，智能體執(zhí)行一個動作at，獲得一個獎勵ut，并將該獎勵反饋給智能體。環(huán)境從而轉(zhuǎn)移成一個新的狀態(tài)st+1. 為了最大化長期的累積獎勵，智能體選擇一系列后續(xù)動作。t時刻的累積折扣獎勵定義如下：

(7)

式中：γ為折扣因子，可對成本函數(shù)進行一定折扣[20]，γ∈(0，1]；ut+k+1為t+k+1時刻的獎勵[18]。

圖3 RL的基本框架Fig.3 Basic framework of RL

AD是一種RL算法[19]。為尋求最優(yōu)動作集，AD將動作集分離到每一個狀態(tài)。通過探索和評估新動作并執(zhí)行，AD不僅避免了動作集的限制、改善了學(xué)習(xí)決策質(zhì)量，還減少了獲取最優(yōu)策略的迭代次數(shù)。AD采用成本函數(shù)p衡量新動作的復(fù)雜度。智能體從狀態(tài)st轉(zhuǎn)移到狀態(tài)st+1的成本為p(st,st+1)。此外，AD采用潛在函數(shù)φ(st)評估新動作。φ(st)可用于精確搜索目標、構(gòu)造獎勵值以及降低采樣復(fù)雜度。采用了潛在函數(shù)φ(st)評估新動作可適用性的公式為

γp(st,st+2)φ(st+2)>(1+δ)γp(st,st+2)φ(st+1)，

(8)

式中：δ為松弛變量，代表探索新動作的保守程度。對于深度神經(jīng)網(wǎng)絡(luò)Q，AD通過最小化損失函數(shù)方式獲得神經(jīng)網(wǎng)絡(luò)的參數(shù)集。損失函數(shù)的定義為

(9)

(10)

(11)

(12)

θi+1為第i+1次迭代時當前網(wǎng)絡(luò)Q的參數(shù)集，θi+j為第i+j次迭代時當前網(wǎng)絡(luò)Q的參數(shù)集，α為學(xué)習(xí)率。通過(11)式和(12)式可周期性地更新網(wǎng)絡(luò)參數(shù)θ和θ-. 在智能體執(zhí)行動作后，根據(jù)當前環(huán)境，在滿足(13)式的情況下更新動作集。

[p(st,st+2)<∞]∧[a(st,st+2)?At(st)]∧
[γp(st,st+2)φ(st+2)>(1+δ)γp(st,st+2)φ(st+1)]，

(13)

式中：At為t時刻的動作集。

2 行星輪軸承剩余壽命預(yù)測方法

2.1 行星輪軸承剩余壽命預(yù)測框架

作為一種新型RNN變體，GRUNN不但能處理時序數(shù)據(jù)或前后關(guān)聯(lián)數(shù)據(jù)，還能緩解常規(guī)RNN在訓(xùn)練過程中可能導(dǎo)致的梯度消失問題。另外，GRUNN特殊的門結(jié)構(gòu)能夠有效地解決長短時間序列上的變化問題。因此，可利用GRUNN從非靜態(tài)和非線性的行星輪軸承振動信號中提取故障特征，用于變工況下行星輪軸承的剩余壽命預(yù)測。CGAN是GAN的一個擴展，它通過額外條件c指導(dǎo)數(shù)據(jù)的生成過程，利用生成器G生成新樣本。因此可將行星輪軸承所處階段看作額外的條件c，指導(dǎo)生成器G生成服從真實數(shù)據(jù)分布的新樣本，從而增加訓(xùn)練樣本數(shù)量，解決訓(xùn)練樣本不足的問題。如果將GRUNN與CGAN相結(jié)合，構(gòu)建一種條件深度循環(huán)生成對抗網(wǎng)絡(luò)(C-DRGAN)，則該深度學(xué)習(xí)模型將具有較強的非靜態(tài)和非線性信號處理能力，并能解決小樣本情況下行星輪軸承的剩余壽命預(yù)測問題。作為一種新穎RL算法，AD將動作集分離到每一個狀態(tài)，尋求最優(yōu)動作集。通過探索和評估新動作，不僅改善了學(xué)習(xí)決策質(zhì)量，還減少了迭代次數(shù)。如果將剩余壽命預(yù)測問題看作智能體的決策過程，則該智能體將根據(jù)目標導(dǎo)向政策采取行動，以取得最佳長期回報。多元線性回歸(MLR)分類器[21]是一種傳統(tǒng)預(yù)測模型。對于非靜態(tài)和非線性信號，MLR無需繁瑣的迭代訓(xùn)練過程與參數(shù)調(diào)整，能獲得精確的預(yù)測結(jié)果。因此，提出一種基于C-DRGAN和AD的行星輪軸承剩余壽命預(yù)測方法。方法框架(見圖4)為：構(gòu)建C-DRGAN，從非靜態(tài)和非線性信號中提取故障特征；采用基于AD的訓(xùn)練算法訓(xùn)練C-DRGAN，提高收斂速度，降低訓(xùn)練時間；根據(jù)訓(xùn)練后的C-DRGAN，利用MLR分類器預(yù)測測試樣本中行星輪軸承的剩余壽命。

圖4 行星輪軸承剩余壽命預(yù)測框架Fig.4 RUL prediction framework of planet bearings

2.2 條件深度循環(huán)生成對抗網(wǎng)絡(luò)

如果將GRUNN與CGAN相結(jié)合，構(gòu)建一種深度學(xué)習(xí)模型，則該模型將同時具備二者的優(yōu)點。基于這個思路，本文開發(fā)一種C-DRGAN. 其模型結(jié)構(gòu)如圖5所示，它主要由條件c、生成器G、判別器D和MLR分類器組成。真實數(shù)據(jù)x為訓(xùn)練樣本。隨機噪聲n與條件c為生成器G的輸入。生成器G由一個GRUNN構(gòu)成。生成器G的輸入為隨機噪聲n. 輸出為服從真實數(shù)據(jù)x分布的生成樣本G(c,n)。生成器G在條件c的指導(dǎo)下，利用隨機噪聲n生成服從真實數(shù)據(jù)分布的新樣本G(c,n)。判別器D由一個GRUNN構(gòu)成。判別器D的輸入為真實數(shù)據(jù)x和生成樣本G(c,n)，輸出為提取的故障特征。這些故障特征作為MLR分類器的輸入，MLR分類器的輸出為預(yù)測結(jié)果。該結(jié)果用于計算獎勵ut，并反饋給生成器G. 在本文中，真實數(shù)據(jù)x為行星輪軸承全壽命周期訓(xùn)練樣本。條件c為行星輪軸承所處階段，指導(dǎo)生成器G生成服從真實數(shù)據(jù)分布的行星輪軸承全壽命周期樣本，增加訓(xùn)練樣本數(shù)量，解決行星輪軸承剩余壽命預(yù)測時訓(xùn)練樣本不足的問題。判別器D用于提取行星輪軸承的故障特征。MLR分類器根據(jù)輸入的故障特征，預(yù)測行星輪軸承的剩余壽命。根據(jù)預(yù)測結(jié)果計算獎勵ut，并利用采用基于AD的訓(xùn)練算法調(diào)整生成器G和判別器D的網(wǎng)絡(luò)參數(shù)。

圖5 C-DRGAN的模型結(jié)構(gòu)Fig.5 Model structure of C-DRGAN

2.3 基于AD的訓(xùn)練算法

RL中，動作集通常是固定的。即使新的動作被發(fā)現(xiàn)，這些新動作也是根據(jù)原動作集來描述的。然而，能改進智能體表現(xiàn)的新動作，很可能既不包含于原動作集，也無法根據(jù)原動作集來描述。因此，通過探索和評估新動作，利用AD尋找最優(yōu)動作集。如果將剩余壽命預(yù)測問題看作智能體的決策過程，則該智能體可根據(jù)目標導(dǎo)向政策采取行動，以取得最佳長期回報。為了改善學(xué)習(xí)決策質(zhì)量，減少迭代次數(shù)，AD可用于訓(xùn)練C-DRGAN。因此，給出一種基于AD的訓(xùn)練算法。主要步驟如下：

步驟1設(shè)置松弛變量δ、折扣因子γ和學(xué)習(xí)率α. 初始化狀態(tài)s0、動作a0和動作集A0.

步驟2設(shè)置dropout率，并將dropout技術(shù)應(yīng)用于C-DRGAN，防止過擬合現(xiàn)象的發(fā)生。

步驟3執(zhí)行動作a0，觀察環(huán)境新狀態(tài)st+1，根據(jù)(7)式計算累積折扣獎勵。

步驟4根據(jù)(14)式計算判別器D的損失函數(shù)，

(14)

式中:Lc為類標簽的損失誤差;Ld為真實標簽的損失誤差;Θ為判別器D的參數(shù)集。

步驟5根據(jù)(15)式計算生成器G的損失函數(shù)，

(15)

式中:Lg為真實標簽的損失誤差;Θ′為生成器G的參數(shù)集。

步驟7根據(jù)(13)式搜索并評估新動作，更新動作集。

步驟8對下一時刻重復(fù)步驟3～步驟7, 直至判別器D和生成器G達到納什均衡。

3 試驗驗證

3.1 數(shù)據(jù)獲取

為了驗證所提方法的有效性，進行了行星輪軸承加速疲勞壽命試驗。圖6為行星輪軸承加速疲勞壽命試驗臺，主要由驅(qū)動電機、行星齒輪箱、負載電機和數(shù)據(jù)采集系統(tǒng)組成。行星輪軸承為NJ304EM圓柱滾子軸承。試驗中通過電路控制負載電機產(chǎn)生3種負載(3 000 N·m、4 000 N·m和5 000 N·m)，驅(qū)動電機的輸出轉(zhuǎn)速分別為400 r/min、600 r/min和800 r/min. 因此，可獲得3種行星輪軸承運行工況：第1種(800 r/min和3 000 N·m)、第2種(600 r/min和4 000 N·m)、第3種(400 r/min和5 000 N·m)。行星齒輪箱上方的加速度傳感器用于采集行星輪軸承運行時的振動加速度信號，采樣間隔為10 s，采樣頻率為25.6 kHz，采樣時間為0.4 s. 當振動加速度信號幅值超過80g時，停止試驗。

圖6 行星輪軸承加速疲勞壽命試驗臺Fig.6 Accelerated fatigue life test rig for planet bearings

3.2 試驗結(jié)果

(16)

圖7 行星輪軸承的全壽命周期振動信號Fig.7 Full lifecycle vibration signal of planet

圖8 行星輪軸承的RRMS值隨時間變化曲線Fig.8 RRMS curve of planet bearing over time

使用的程序開發(fā)框架為Tensorflow1.1.0，編程語言為Python. 計算機配置為8核i7-6700處理器，16 GB內(nèi)存。根據(jù)3種運行工況下的6組行星輪軸承全壽命周期訓(xùn)練樣本，構(gòu)建用于行星輪軸承剩余壽命預(yù)測的C-DRGAN. 該模型由具有2個GRU層的生成器G、具有兩個GRU層的判別器D和一個MLR分類器組成。GRU層的神經(jīng)元數(shù)目設(shè)為240，輸入數(shù)據(jù)為45×45矩陣。通過基于AD的訓(xùn)練算法，采用訓(xùn)練樣本訓(xùn)練C-DRGAN. 噪聲比例設(shè)為0.3，松弛變量δ設(shè)為0.1，折扣因子γ設(shè)為0.9，dropout率設(shè)為0.1，學(xué)習(xí)率α設(shè)為0.001. 根據(jù)訓(xùn)練后的C-DRGAN，利用MLR分類器預(yù)測測試樣本中行星輪軸承的剩余壽命。由于MLR分類器的輸出為包含多個元素的列向量，該列向量的元素用于擬合測試樣本的RRMS值隨時間變化曲線。均方根誤差(RMSE)是一種常用的軸承剩余壽命預(yù)測方法效果評價指標。為了與其他方法進行對比，本文采用由RMSE計算獲得的預(yù)測準確率評估本文提出方法的效果。預(yù)測準確率的計算公式為

(17)

式中：eRMSE為均方根誤差；yI和I分別為第I個檢查點剩余壽命的真實值和預(yù)測值；N為檢查點個數(shù)。3種運行工況下行星輪軸承的剩余壽命預(yù)測準確率如表1所示。從表1中可以看出，負載越大，轉(zhuǎn)速越高，預(yù)測效果越好。當負載電機產(chǎn)生5 000 N·m負載且驅(qū)動電機的輸出轉(zhuǎn)速為400 r/min時，測試樣本預(yù)測準確率超過98%. 主要原因在于從較大負載和較高轉(zhuǎn)速行星輪軸承的訓(xùn)練樣本中獲取的故障特征更具特點，有助于預(yù)測測試樣本中行星輪軸承的剩余壽命。另外，在小樣本情況下每種運行工況的平均準確率均超過96%. 這是因為該方法在行星輪軸承所處階段的指導(dǎo)下，利用生成器G生成大量新樣本，從而解決MLR分類其訓(xùn)練不充分的問題。因此，該方法能在小樣本情況下準確地預(yù)測行星輪軸承的剩余壽命。

表1 3種運行工況下行星輪軸承的剩余壽命預(yù)測準確率Tab.1 RUL prediction accuracies of planet bearings underthree operating conditions

3.3 對比分析

因行星輪軸承的剩余壽命預(yù)測準確率主要受GRU層神經(jīng)元數(shù)目的影響，神經(jīng)元數(shù)目對預(yù)測準確率影響的對比分析如下。改變第1個GRU層神經(jīng)元數(shù)目，且第2個GRU層神經(jīng)元數(shù)目為第1層的一半。第1個GRU層神經(jīng)元不同數(shù)目下的預(yù)測結(jié)果如圖9所示。從圖9中可以看出，訓(xùn)練樣本準確率可達100%，測試樣本準確率超過95%. 但隨著第1個GRU層神經(jīng)元數(shù)目的增加，訓(xùn)練時間逐漸延長。主要原因在于C-DRGAN的計算復(fù)雜度逐漸增加，延長了訓(xùn)練時間。當?shù)?個GRU層神經(jīng)元數(shù)目超過350時，測試樣本準確率保持穩(wěn)定，而訓(xùn)練時間明顯增加。綜合考慮預(yù)測準確率和訓(xùn)練時間后，將第1個GRU層神經(jīng)元數(shù)目設(shè)定為350.

當?shù)?個GRU層神經(jīng)元數(shù)目設(shè)為350時，改變第2個GRU層神經(jīng)元數(shù)目。第2個GRU層神經(jīng)元不同數(shù)目下的預(yù)測結(jié)果如圖10所示。由圖10可見，測試樣本準確率先逐漸提高，然后保持穩(wěn)定。當?shù)?個GRU層神經(jīng)元數(shù)目達到200時，測試樣本準確率達到98.43%. 因此可將第2個GRU層神經(jīng)元數(shù)目設(shè)定為200.

圖9 第1個GRU層神經(jīng)元不同數(shù)目下的預(yù)測結(jié)果Fig.9 RUL predicted results with different neuron numbers of the first GRU layer

圖10 第2個GRU層神經(jīng)元不同數(shù)目下的預(yù)測結(jié)果Fig.10 RUL predicted results with different neuron numbers of the second GRU layer

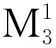
圖11 行星輪軸承的剩余壽命預(yù)測結(jié)果Fig.11 RUL predicted results of planet bearing

為了研究本文C-DRGAN方法的收斂性，分別采用Adam優(yōu)化算法、基于行動者- 評論家(AC)的訓(xùn)練算法和基于AD的訓(xùn)練算法訓(xùn)練C-DRGAN. 在Adam優(yōu)化算法中，dropout率設(shè)為0.1，學(xué)習(xí)率α設(shè)為0.001，兩個矩估計指數(shù)衰減率β1和β2分別設(shè)為0.9和0.99，數(shù)值穩(wěn)定常數(shù)ε設(shè)為10-8. C-DRGAN的模型結(jié)構(gòu)和基于AD訓(xùn)練算法的參數(shù)設(shè)置如前所述。基于AC訓(xùn)練算法的參數(shù)設(shè)置與基于AD訓(xùn)練算法的相同。預(yù)測準確率與迭代次數(shù)之間的關(guān)系曲線如圖12所示。從圖12中可以看出，當?shù)螖?shù)超過320時，基于AD訓(xùn)練算法的預(yù)測準確率便趨于穩(wěn)定，表明該算法能顯著地提高C-DRGAN的收斂速度。主要原因在于該算法避免了動作集的限制，使智能體根據(jù)目標導(dǎo)向政策采取行動，以取得最佳長期回報，從而減少了獲取最優(yōu)策略的迭代次數(shù)，降低了訓(xùn)練時間。

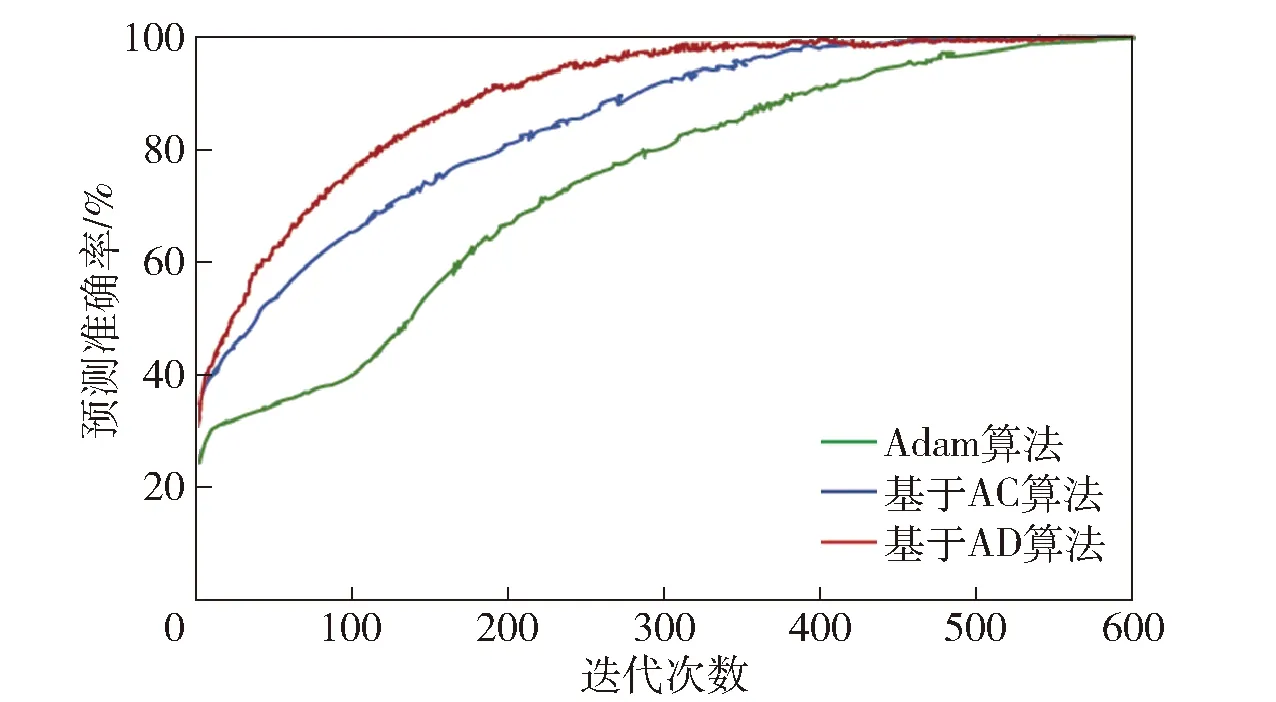
圖12 預(yù)測準確率與迭代次數(shù)之間的關(guān)系曲線Fig.12 Relation between RUL predicted accuracy and number of iterations

為了進一步驗證本文方法對行星輪軸承剩余壽命預(yù)測的效果，將該方法與Paris模型、Wiener過程模型和SVM進行對比。利用時間分段算法訓(xùn)練Paris模型[5]；通過極大似然估計算法獲得Wiener過程模型的參數(shù)[8]；采用遺傳算法選取SVM的核函數(shù)和懲罰參數(shù)。訓(xùn)練與測試樣本數(shù)之比分別為1∶5，1∶2，1∶1和2∶1，4種方法的預(yù)測結(jié)果如圖13所示。由圖13可看出，訓(xùn)練與測試樣本數(shù)之比越大，預(yù)測準確率越高。這是由于越多的訓(xùn)練樣本可使模型得到充分訓(xùn)練。在不同樣本數(shù)之比下，該方法均取得最佳的預(yù)測效果。原因在于該方法將行星輪軸承所處階段看作額外的條件，指導(dǎo)生成器生成服從真實數(shù)據(jù)分布的新樣本，從而增加訓(xùn)練樣本數(shù)量，解決訓(xùn)練樣本不足的問題。因此，該方法能取得較高的行星輪軸承剩余壽命預(yù)測準確率。

圖13 4種方法的預(yù)測結(jié)果Fig.13 RUL predicted results of four methods

4 結(jié)論

1)本文提出的C-DRGAN方法利用CGAN，在已知運行工況指導(dǎo)下生成服從真實數(shù)據(jù)分布的訓(xùn)練樣本，從而在小樣本情況下取得出色的行星輪軸承剩余壽命預(yù)測效果。

2)C-DRGAN方法利用GRUNN的狀態(tài)記憶和時變信號的處理能力，從非靜態(tài)和非線性信號中提取故障特征，解決了變工況下行星輪軸承的剩余壽命預(yù)測問題。

3)C-DRGAN方法采用基于AD的訓(xùn)練算法訓(xùn)練C-DRGAN，避免了動作集的限制，使智能體根據(jù)目標導(dǎo)向政策采取行動，以取得最佳長期回報，從而減少了獲取最優(yōu)策略的迭代次數(shù)，降低了訓(xùn)練時間。