四旋翼飛行器軟件設計*

馬亨杰，王碩之

（1.閩江學院計算機與控制工程學院，福建 福州 350108；2.廈門理工學院電氣工程與自動化學院，福建 廈門 361012）

1 引言

1907年，在Charles Richet教授的幫助下，Breguet兄弟進行了第一次旋翼機的設計嘗試，并設計出“Gyroplane No.I”（旋翼機一號）?！靶頇C一號”的機身由鋼管搭接構成，中心配備一個供駕駛員使用的座椅和部分動力裝置，四個鋼索支撐的鋼管臂從中間向四個方向延伸，每個支撐臂末端都有一對同軸相疊的四葉片轉子。兩個轉子組順時針旋轉，兩個逆時針旋轉。同時，為了克服扭矩效應，相同旋轉方向的轉子組間隔安裝在支撐臂末端[1]。

從近年的發展趨勢來看，四旋翼飛行器漸漸由體積龐大的鋼架結構轉向輕便、迷你結構，越來越多的工程作業會考慮加入四旋翼飛行器進行輔助勘測。同時，為滿足工程所需要的作業能力，通過對通訊技術、開發環境、可操作性等諸多方面的研究探索，技術人員提高了四旋翼飛行器的穩定性、靈敏度等性能[2]。

為了進一步提高飛行器的穩定性、靈敏度，本文采用了卡爾曼濾波和PID算法?？柭鼮V波的測量結果隨時間變化，包含統計噪聲和其他不定雜波，并產生未知變量的估計值，而PID算法是一種較為常用的自動控制算法。本文中，控制模塊的前期姿態融合算法采用卡爾曼濾波，后期算法則采用PID算法來做最終的姿態控制[3]。并在最后對該算法進行了實驗與測試。

2 四旋翼飛行器軟件設計

2.1 卡爾曼濾波

卡爾曼濾波是一種算法濾波，它的測量結果隨時間變化，包含統計噪聲和其他不定雜波，并產生未知變量的估計值[4]。這些估計值基于通過估計每個時間范圍內變量的聯合概率分布，單獨進行單一測量。卡爾曼濾波器可以寫成單個方程，但它通常按照概念不同，分為2個不同的階段：“預測”和“更新”。預測階段使用來自之前時間單元的狀態來估計當前時間單元的狀態，在更新階段，當前的先驗預測與當前的觀測信息相結合以改進狀態估計，這個改進的估計被稱為后驗狀態估計。

本文選用卡爾曼濾波算法（圖1），是因為在實際情況下我們無法直接獲得飛行器的準確姿態，而利用卡爾曼算法可以算出四軸當前的準確姿態，從而達到提升飛行器飛行的平穩程度及靈敏程度，更便于地面控制者的操作，達到靈敏、穩定的效果。 涉及卡爾曼濾波算法，先要討論基準點的確立。陀螺儀得到±250范圍的數據來表示轉動角速度。需要額外注意的是，±250的數據需要將原始數據減去基準點數據之后得到的。

上文提及的基準點指的是傳感器處于零負荷時候的輸出數據。例如反應的Rol、Pit、Yaw三個方向的轉動角速度，如果陀螺儀沒有轉動，則輸出為0。但是在實際情況下，考慮環境干擾等因素，通常會有初始值。因此需要進行標零，即在四旋翼飛行器起飛前水平放置進行標零，確立水平面。初始化完成之后，將得到的姿態傳感器數據輸入到相應的姿態解算算法中，以便于計算四軸的準確姿態。

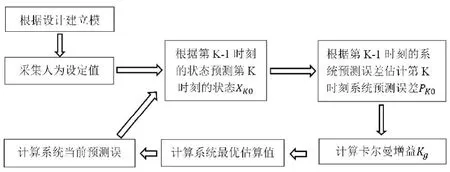
圖1 卡爾曼濾波算法流程圖

下面以橫滾方向姿態變量Reading_IntegralGyroRoll為例，分析在這種算法中數據的產生和處理過程。 第1步：存儲采集數據與放大加速度計采集的數據。將采集到的數據進行正反向設置和減去中立點操作，并重新用新的變量名為上述數據進行存儲。這樣做的優點在于新的數據仍舊可以被存儲在原本的變量名中，且對新的變量名進行處理之后可以方便清除已經使用過的數據，從而達到存儲空間的相對優化利用。

第2步：將陀螺儀和加速度計的數據都進行積分處理。并且與后面的長期融合計算得出的誤差修正量進行校正補償。進行了初步積分計算處理之后，設定一個變量balance_number為對初步積分計算的結果的采樣次數，并且進行多次采樣。當采樣次數超過2^8（256）次之后，進行長期融合處理，即：將所得數據設定修正為長期數據。

第3步：對于陀螺儀數據的積分結果再次進行積分。

第4步：短期數據融合。用加速度傳感器采集的瞬時數值乘以系數，來修正陀螺儀采集數據的積分。接著輸入PID調節器中，控制電機依據合適的功率轉動。

第5步：長期數據融合。當短期融合次數達到了所定義的次數，接著執行長期融合。設定一個長期融合后得到的變量AttitudeCorrectionRoll。長期融合的處理結果，是計算統計出AttitudeCorrectionRoll并且在采樣的同時對陀螺儀采集的數據進行實時修正。值得注意的是，長期融合對于不同的機械結構（如不同大小的機架）使用類似算法的適用性有很顯著的提高，且對積分穩定不漂移有不小的貢獻。長期融合的基本思路是將陀螺儀采集的數據的積分結果再次積分，后執行衰減，再與加速度計采集的數據進行比較。從而得出較為準確的漂移誤差，并最終修正到采樣瞬時值中，執行對積分數值的累加修正。

第6步：基準點修正。上述文章提及了基準點的重要作用，及重要價值。在實際環境中，不可避免會產生由溫度、噪聲等引起的誤差，導致基準點漂移。所以對于基準點執行實時修正補償對于提高整個系統穩定性是非常有幫助的?；鶞庶c的修正補償原理是，在到達了BALANCE_NUMBER的采樣次數后，執行短期融合與長期融合的修正補償之后，對比原始與執行修正之后的基準點參數信號，如果差距過大，則判斷是基準點的漂移導致。根據其偏差的正負判斷執行基準點修正的方位。

第7步：Yaw/Rud軸數據處理。Yaw參數代表水平旋轉。對于姿態校準調節來說，Rol與Pit作用相對Yaw較強，所以優先考慮Rol與Pit的調節執行，即：優先考慮Rol與Pit的卡爾曼濾波算法執行。完成之后，本設計對于Yaw的瞬時值與積分值進行計算。

至此，基于卡爾曼濾波的姿態數據處理基本完成。得到了較為準確客觀且具有代表性的實際姿態數據。如下：橫滾姿態數據：Reading_IntegralGyroRoll；俯仰姿態數據：Reading_IntegralGyroNick。需要注意的是，上述兩個處理之后的數據并非真實的旋轉角度，而是隨著最終旋轉角度的增加而增加，且具有較好的跟隨性與隨動性。

2.2 PID算法及機體坐標系建立與分析

⑴ PID控制算法設計

PID算法是一種較為常用的自動控制算法，控制模塊的前期姿態融合算法會采用卡爾曼濾波，后期算法則會采用PID算法來做最終的姿態控制[5]。

PID算法在四旋翼飛行器上的本質就是把采集到的數據和參考數據相減（圖2），然后把此差值應用到系統的輸入值，系統輸入值就會讓系統數據達到或保持在設定的參考值范圍內。PID控制器具有結構簡單、穩定性好、計算方便等優點。

離散系統中的位置式的PID表達式為：

公式中，KP、Ki、Kd分別為比例、積分、微分系數。error是“設定值減去當前值”。

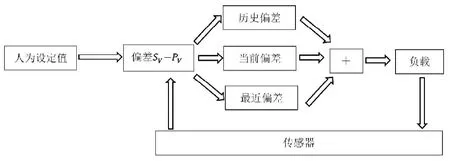
圖2 PID算法流程圖

在采集的數據計算中，seted為目標姿態，由遙控段設定，即：人為控制。從物理角度看，seted在最終PID表達式中對姿態控制起到正反饋作用。當seted數值變化的時候，經過PID調節器的計算，四旋翼飛行器的姿態會跟隨seted的方向而變化。實際姿態數據在經過PID計算處理之后，對平衡的保持充當負反饋的作用。PID的算法過程簡單來說就是不斷地去調整設定的數值（人為操控的輸入值）與實際姿態的通過前文卡爾曼濾波后的數值之間的關系。通過KP、Ki、Kd分別為比例、積分、微分三個角度來修正這一誤差。且形式與二階運算的解結構類似，因此使用PID算法控制二階系統（電機控制系統為二階系統）符合控制方程，可以較好的執行所需的控制任務。

本設計中陀螺儀、加速度傳感器、磁力計都是有本身特有的參考系的，換言之，都是有方向的。當這3個與姿態采集相關的傳感器均焊接到PCB板上后，以它們為基準建立坐標系。姿態數據從3個傳感器采集的信息讀取。焊接完畢之后，根據標志點位置推到各個傳感器X、Y、Z軸的位置，并根據讀取數據決定是否要對數據進行取反。

第1步：從力學角度分析得出最終控制電機的方式表達式。將四旋翼飛行器的姿態量抽象為Ail（橫滾）、Ele（俯仰）、Rud（偏航）、Thr（油門）四個量，每個量包含seted和real作差以及PID算法。

第2步：根據表達式推出人為控制的方向設置。在將人為控制信號輸入到PID調節器并執行PID算法前，需要將其方向調整，以至符合上文中的力學表達式。

第3步：根據力學表達式推出四旋翼飛行器運動的陀螺儀坐標系?？紤]到陀螺儀是基礎的姿態采集傳感器，所以本設計將重點放在陀螺儀坐標的推導。根據手冊標志點，將陀螺儀的坐標系與四旋翼飛行器坐標系關聯，再根據力學表達式，推算陀螺儀采集信號是否需要取反。

第4步：加速度傳感器的方向的正負設置。三軸加速度傳感器有自身的坐標系，在構建機體坐標的過程中，判斷依據主要有兩種方式，分別是基于四元數法的姿態判斷、基于卡爾曼濾波的姿態判斷。前文提到，本設計主要采用卡爾曼濾波算法，所以下面主要討論基于卡爾曼濾波算法的處理方式。根據陀螺儀與加速度傳感器方向，確定補償數據組。考慮到陀螺儀的動態特性較好，加速度傳感器的靜態特性較好，所以采用加速度傳感器來補償陀螺儀的漂移[6]。將加速度傳感器采集的三個軸數據表示為Acc_Rol、Acc_Pit、Acc_Yaw，從而能更好地與陀螺儀采集的Rol、Pit、Yaw所對應。當陀螺儀沿著一個方向轉動時候，加速度傳感器的某一個軸的數據信息如果產生相應的變化，則這兩個數據成為一個“補償數據組”互相補償，最終起到修正校準陀螺儀姿態數據偏差的作用。完成之后開始PID表達式的參數構建。

前文介紹了電機控制表達式，陀螺儀轉動的角速度代表瞬時變化，加速度傳感器采集的數據積分后得出的數據直接選作積分項。具體PID調節器構造過程如下：

第1步：計算errorn項（比例項）。errorn代表當前時刻人為給定的姿態與實際姿態的誤差，用遙控器數據減去陀螺儀姿態數據來表示。采用人為給定數據減去陀螺儀姿態采集數據。需要注意的是，人為給定坐標系與姿態傳感器方向需要考慮同向或者反向的問題，從而決定程序中是加號還是減號。

第2步：計算error1+error2+…+errorn（積分項）。積分項代表陀螺儀采集的旋轉角速度在四旋翼飛行器長期作用的結果，可以表示四旋翼飛行器當前姿態角度。采用經過卡爾曼濾波處理的橫滾姿態數據：Reading_IntegralGyroRoll；俯仰姿態數據：Reading_IntegralGyroNick這兩組數據。這樣處理的好處是相較于直接采用第一步中的errorn進行積分來說，漂移較小[7]。

第3步：計算errorn-errorn-1（微分項）。每次對errorn執行算術處理之后將處理結果存儲為新的變量名dataOld。在下一個處理的周期中，用新的采樣數據減去dataOld得到errorn-errorn-1項。

第4步：加入KP、Ki、Kd等系數。將式中的三個參數與前三步步求得的各項分別對應相乘，所得值設定為OutPutdata表達式，并最終引用于電機控制表達式。

第5步：互補濾波。本次計算處理完成后，增加互補濾波。即，對每次運算處理的結果都與前一次結果進行加權平均。

⑵ PID算法各參數的整定

為了使得PID調節器獲得較好的調節效果，除了姿態數據積分處理要準確外，還需著重關注KP、Ki、Kd三個參數的整定校準。本設計將參數的整定分為2步，第1步為估算，第2步為配湊。估算過程是根據之前各個數據的范圍執行理論估算，配湊過程需要不斷的進行測試并根據結果進行最理想的配湊。需要注意的是KP、Ki、Kd系數的作用也需要先有定性的了解。

比例系數KP：KP系數一直對執行調節起作用，KP過小會導致系統執行調節不夠明顯、不夠有力，過大則會導致系統出現振蕩。本設計的具體調節為先設置較大的KP，然后逐漸減小并觀察，當出現振蕩時將當時的KP乘以0.717（經驗數據），此時得到的數值再進行執行并觀察有無振蕩，如此循環直至系統不再出現明顯振蕩。

積分系數Ki：Ki主要與PID算法后期的平滑處理與收斂有關聯，主要影響的是響應曲線中實際值接近定值后的部分的平滑程度，平滑程度越高系統的精細度越好。具體作用在本設計的直觀結果，為在四旋翼飛行器較為穩定的狀態下如果出現小范圍偏移，則調大Ki；如果出現振蕩且較振蕩較大，則調小Ki。

微分系數Kd：增加系統的快速反應能力，增加收斂時刻的振幅。在具體調節中，有振蕩則調小，反饋弱則增大。

3 實驗與測試

本章主要根據設計的需要對系統環節的可靠及可行性進行實驗與測試。由于本設計將PID控制比例設置為可通過Android上位機進行調節所以本設計直接進行實物調試。

3.1 Android上位機通訊實驗

首先，打開四旋翼飛行器總開關，確保藍牙通訊模塊紅燈閃爍，表示處于開放狀態打開Android上位機的應用程序并進行連接藍牙，本設計的藍牙標識為BT04-A。藍牙匹配連接成功后，四旋翼飛行器搭載的藍牙模塊紅燈顯示常亮，Android應用顯示“藍牙已連接到BT04-A”字樣。

3.2 Android上位機控制電機測試

在Android上位機應用程序上打開電調控制測試開關，并觀察四旋翼飛行器各電機運行情況（需要在測試前拆除機翼）。

3.3 Android上位機校準陀螺儀磁力計

打開Android上位機界面，開啟校準模式。放平四旋翼飛行器，點擊校準加速度計。觀察顯示的傳感器數據（圖3）。

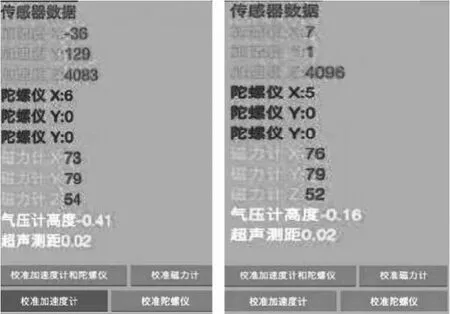
圖3 校準測試前（左）、后（右）

3.4 飛行姿態自平衡測試

本設計對于姿態反饋的測試主要先測試低油門下單電機對于姿態的調節，后加大油門至30%油門觀察對軸的自我穩定情況，后進行實際測試。具體步驟如下：

首先將對軸進行非剛性固定，本設計采取用無彈性的繩子綁住一對軸的機架部分，將剩余一對的電機取一端放置最低點，另一端為最高點。加大油門至5%，漸漸放平。觀察低處電機在放平之前有無轉動（圖4）。

接著，加大油門至30%，輕微觸碰自由對軸的一端，讓其偏離水平，然后觀察四旋翼飛行器能否回到平穩狀態。本設計期望在四旋翼飛行器在油門5%的前提下，與水平夾角50°左右能有明顯的響應，實驗后確定PID增益為設定區間的40%左右。

圖4 對姿態反饋控制的測試

圖5 Android上位機控制飛行器起飛

3.5 與Android上位機的姿態同步

在空曠地帶進行與Android上位機的姿態同步測試，改變搭載Android系統的移動端角度，觀察四旋翼飛行器能否跟隨移動端控制（圖5）。

4 結論

隨著工程作業目的越來越復雜，作業環境越來越特殊，四旋翼飛行器在各個領域有了更廣泛的應用，同時工程研究項目對四旋翼飛行器可靠性靈敏度、以及便攜程度都有了更高的要求。四旋翼飛行器的進一步簡便化、輕量化的研究對于工程實踐有著很高的戰略意義。

本文綜述了四旋翼飛行器的發展概況和發展趨勢，并將卡爾曼濾波和PID算法相結合，設計出了四旋翼飛行器軟件，實現了現代飛行器所需要的便捷化、高靈敏度、高精度等特點，并在最后進行了該設計的可靠及可行性進行的實驗與測試，得出了該方案高效可行的結論。