深度教學：指向學生思維深處的路標

王玉英

【摘 要】深度教學是觸及知識內核和走進思維深處的教學。針對人教版數學三年級下冊第61頁“認識面積”中的探究性問題“3×4，2×5兩個長方形的面積，孰大孰小”，學生用重疊法比較一次，發現無法解決問題。筆者在課堂上與學生進行深度討論，引發一場用升級版重疊法比較面積大小的“頭腦風暴”。結果表明，我們不僅找到了“剪裁+兩次重疊”與“畫線+兩次重疊”兩種解決辦法，還借助乘法分配律和圖形操作關系式揭示了“多次重疊”背后的數學原理，進而從數形結合的角度深化了對面積本質的理解，促使學生思維走向深處。

【關鍵詞】面積 重疊法 數學原理 質疑 深度教學

一、深度教學之課前慎思

好問題是開啟深度教學之門的鑰匙，也是激發學生深刻思維的催化劑。在“認識面積”教學中，教材讓學生探究3×4和2×5兩個長方形的面積大小。一名學生用眼睛觀察后，說：“看不出哪個面積大。”另一名學生用重疊法比較一次，然后說：“用重疊的方法也比較不出來，怎么辦呢？”教材發問的目的是引出數方格法，但是重疊法真的無效嗎？學生用重疊法比較一次，發現無法解決問題。那么，用重疊法比較多次，能解決嗎？這引起了筆者的深思，進而提出系列化環環相扣、引人深思的好問題。

（1）什么是重疊法？用重疊法比較面積大小體現了面積的哪個特征？什么樣的圖形用重疊法比較一次，就能比較出面積大小？

（2）用重疊法比較一次，不能解決的，比較多次，能解決嗎？若能，需要比較幾次？是有限次嗎？

（3）如何設計深度有效的活動，多次重疊就能解決問題？該活動破壞圖形的完整性嗎？若破壞，又該如何改進？（如長方形鋼板，不能破壞其完整性）

（4）“多次重疊”背后的數學原理是什么？又蘊含著什么數學思想？這些原理和思想能被小學生理解和領悟嗎？

（5）對于更一般的兩個長方形，有限次重疊，能否比較出它們的面積大小？在理論上能否給出相應的證明？能否設計出一個高效的算法，編程后讓計算機解決該問題？為解決上述問題，筆者和學生在課堂上動手又動腦，帶來了一場別樣的、富有深度的精彩盛宴。

二、深度學習之精彩回放

學生真正的“深度學習”是指在教師的引領下，學生圍繞挑戰性的問題，全身心積極參與、體驗成功、獲得發展的學習過程。在課堂上，師生借助“頭腦風暴”讓問題得以解決、原理得以清晰、知識得以內化，把思維引向深處。

【片段1】

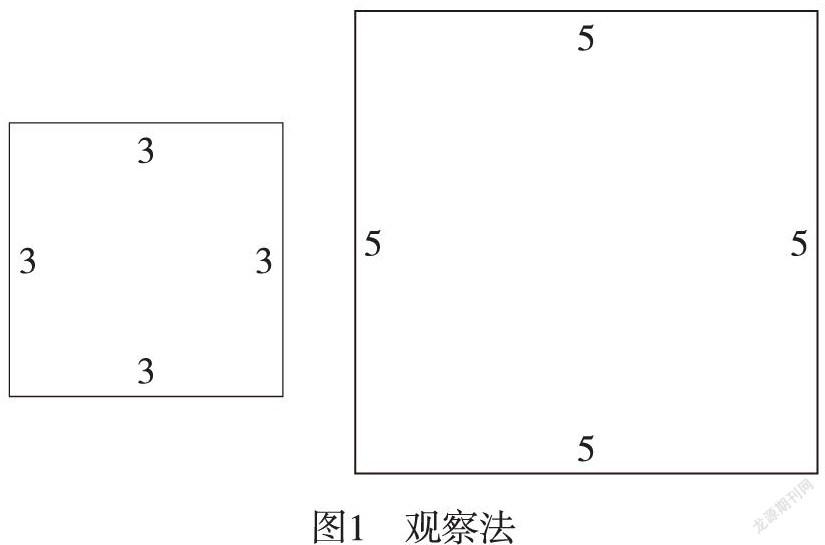
通過觀察法比較，讓學生體會“面積大小”，形成面積表示“一塊區域大小”的表象。通過一次重疊，讓學生理解“面積的可加性”。

師：剛才我們通過看面、摸面、畫面活動，對面積有了初步的認識。那么，你能比較這些圖形的面積嗎？（出示3×3和5×5兩張正方形紙片）

生：一看就知道右邊的紙片大。

師：右邊的紙片大，意味它所占的區域——大。紙片大，也就是它的面積——大。所以，面積表示——

生：一塊區域的大小。

師：差別較大的圖形，用觀察法就能看出面積大小。那這兩張紙片呢？（出示3×4和3×5兩個長方形紙片）動手試一試吧。

（發給學生紙片，小組合作探究總結）

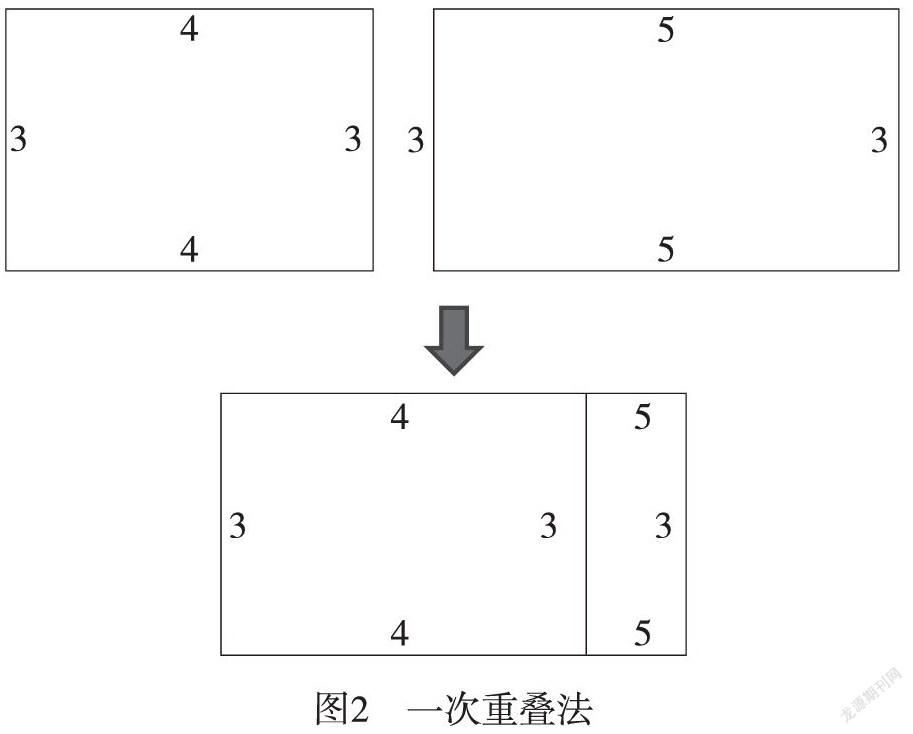
生：移動紙片，把它們的邊對齊，發現右邊的紙片大一點。（同步演示）

師：重疊部分紙片，剩余的部分決定它們的大小，對嗎？

生：對。

師：這說明，較大的紙片分成了兩部分，哪兩部分啊？

生：重疊的部分和剩余的部分。

師：這兩部分的面積之和與原來紙片的面積相等嗎？

生：相等。

師：這是從求和的角度表述的。如果換成做差的角度，又該怎么表述呢？

生：原來紙片的面積減去重疊部分的面積就是剩余部分的面積。

師：你發現這兩張紙片的邊有什么特點？

生：有一對邊能完全重合，說明這對邊長相等。

【片段2】

針對用一次重疊無效的情形，創造性提出“剪裁+多次重疊”與“畫線+多次重疊”的兩種解決辦法，引發一場比較面積大小的“頭腦風暴”活動。

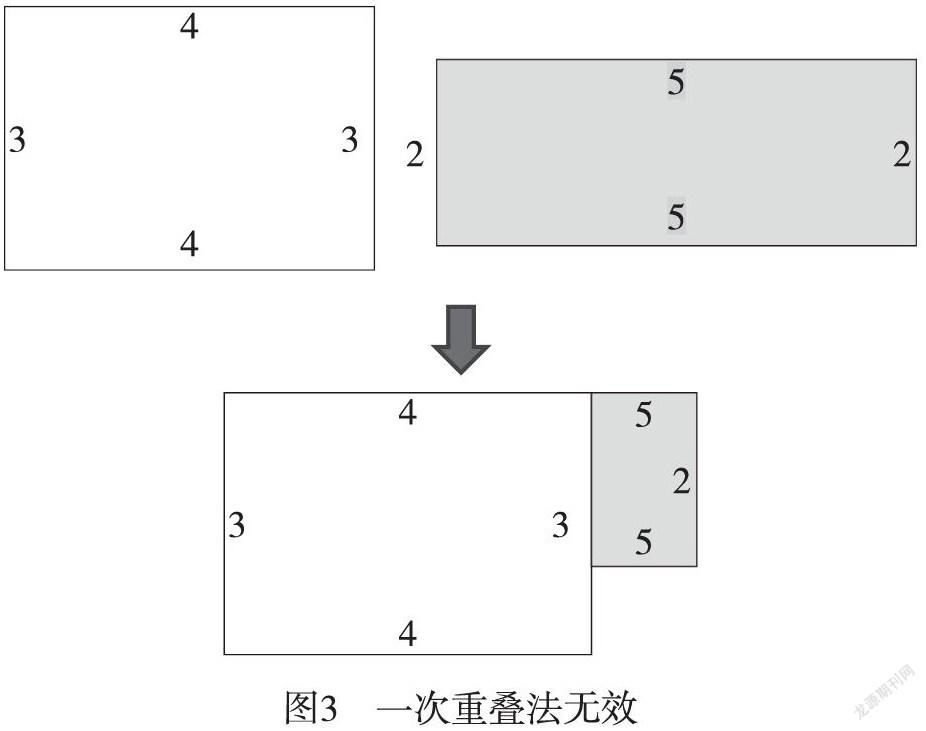
師：有相等邊長的長方形，重疊法很有效。那么，這兩張紙片，用重疊法還能比出大小嗎？（出示3×4和2×5兩張長方形紙片）

生（滿懷信心，邊演示邊說）：移動紙片，直角邊對齊，部分重疊起來，剩余的部分哪個大呢？

（學生陷入困局，百思不得其解時，教師點撥）

師：理論上，要減去重疊部分的面積，那么，在操作中，你怎樣做呢？給你一把剪刀，手腦并用，嘗試一下。

（學生嘗試后，恍然大悟）

生：我有辦法了，剪掉重合的部分，再看剩余的部分，誰的面積大。

師：剩余的部分，再怎么比較啊？

生：還用重疊法啊。

師：要是還比較不了，怎么辦啊？

生：再剪掉重合的部分，再用重疊法比。

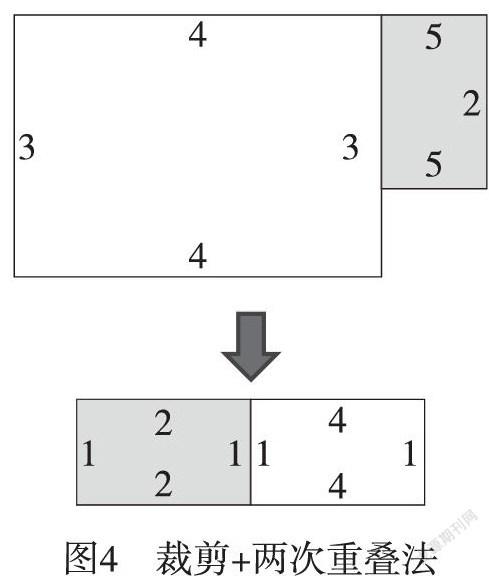
師：反復剪掉重合的部分，直到能用重疊法比較為止。（見圖4）用這種方法再試試吧！

師：你們用了幾次重疊法？

生：兩次。

師：這與普通的重疊法（重疊一次）不同。所以，我們找到了一種新方法，老師給它起名為“剪裁+多次重疊法”，你同意嗎？

生：同意。

師：這種方法雖然能比較出面積的大小，但是完整的紙片被剪碎了，破壞了紙片的完整性。很多材料，如鋼板，不能破壞它的完整性，又該怎么辦？

（學生再次陷入困局， 教師再次點撥）

師：你們怎么剪，沿著誰的邊緣？

生：重合部分的邊緣。

師：可是這個邊緣不能破壞啊。

（學生似乎有所明白，教師繼續點撥）

師：這個邊緣起到什么作用？是將圖形分成兩部分嗎？

生：是的。

師：那不就是“分界線”嗎？

生：不破壞“分界線”？那我在鋼板畫一條線代替“分界線”，不就可以了嗎？

師：對啊，反復沿著重疊的邊緣畫線，直到能用重疊法比較為止。（見圖5）給這種方法起個名字，叫——“畫線+多次重疊法”。又是一個好方法。

（學生鼓掌）

【片段3】

借助乘法分配律和鏈式關系圖揭示“多次重疊”背后的數學原理，讓學生體會“形使數直觀，數使形入微”。

師：這兩種方法都需要“多次重疊”。那么，“多次重疊”背后涉及什么數學知識，你知道它的數學原理嗎？

原理探究，步驟如下：

① 給出長方形的符號記法。如2×5長方形紙片，記為或 。

② 標出紙片的邊長。

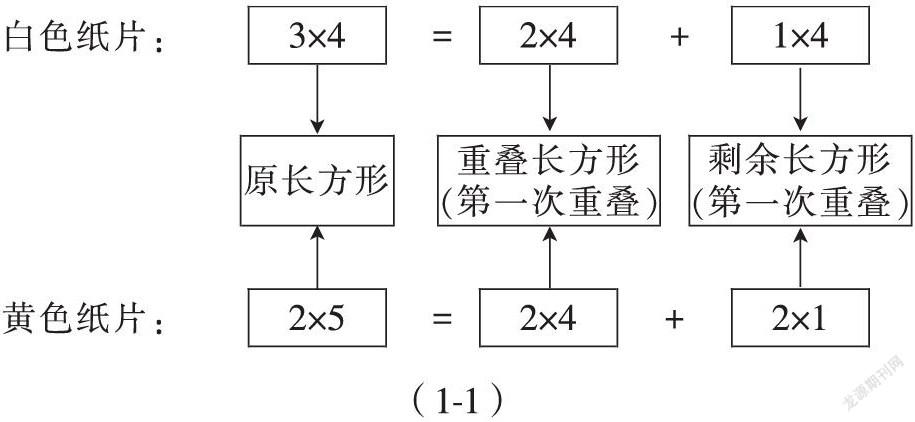
③ 兩紙片第一次重疊，得圖4（上）。

④ 利用片段1中“原面積、重疊面積、剩余面積的關系”，第一次重疊對應的圖形操作關系式為

其中，“+”表示圖形合并，“=”表示圖形拆分或組合。

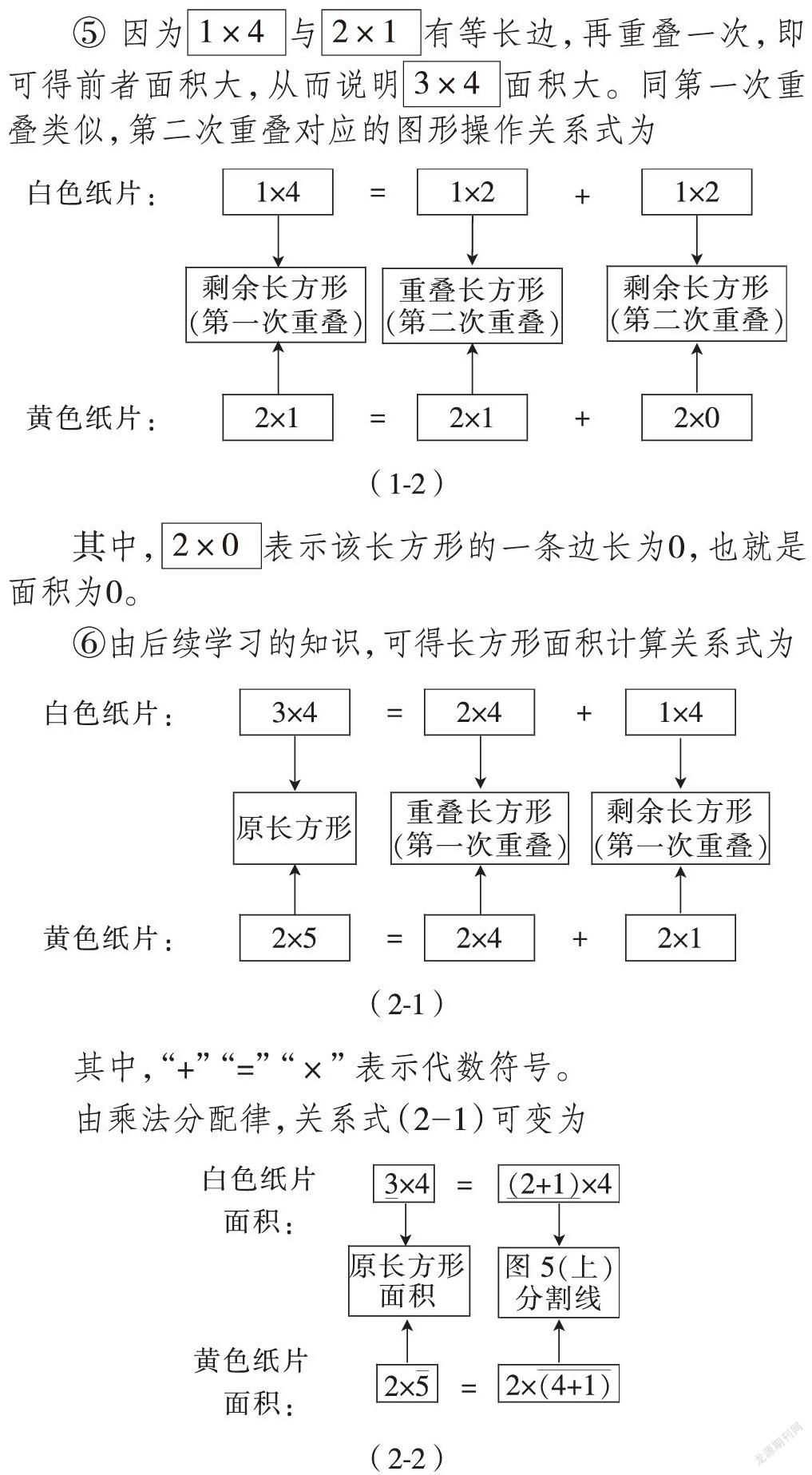
⑤ 因為與有等長邊，再重疊一次，即可得前者面積大，從而說明面積大。同第一次重疊類似，第二次重疊對應的圖形操作關系式為

其中，表示該長方形的一條邊長為0，也就是面積為0。

⑥由后續學習的知識，可得長方形面積計算關系式為

其中，“+”“=”“×”表示代數符號。

由乘法分配律，關系式（2-1）可變為

其中，中 “+”除表示兩數字相加外，還可表示原來的邊被截成兩段，見圖5（上）。

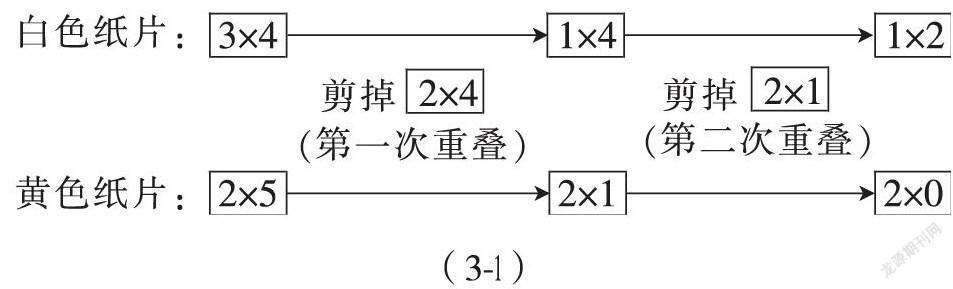
⑦ 操作關系式（1-1）和（1-2）是分步的。合并后，用鏈式表示為

其中，“”指向剩余的長方形。 鏈式關系式更能直觀、清晰地描述圖形的分割操作，便于判斷原圖形面積的大小。

師：一般來說，每次重疊都會有兩種情形，它們對應的重疊圖形也不同。針對另一種情形，你能一邊操作圖形，一邊寫出它的鏈式關系式嗎？

三、師生成長之課后深思

新課程賦予教師新的內涵和新的要求。教師不再是傳統的“傳道、授業、解惑”者，更不是用現成設計的教案去完成知識傳授目標的傳遞者。進入新世紀，教師理應成為教育教學工作的探索者、研究者。課后深思，則是教師成長的必經之路。

“面積”是平面幾何的一個基礎概念，而“認識面積”更是整個面積教學的“種子課”。為促進種子的生根、發芽，我們在教學中要深耕細作，不怕花時間。教材上“用重疊的方法也比較不出來”這句話，像是一只亞馬孫雨林中的蝴蝶，扇動幾下翅膀，就引發了一場用升級版重疊法比較面積大小的“頭腦風暴”，形成了現實版的蝴蝶效應：

（1）在課堂上，師生通過手腦并用、思維沖擊和思想碰撞，創造性提出比較面積大小的兩種方法，即剪裁+多次重疊（破壞圖形完整性）和畫線+多次重疊（保持圖形完整性）。學生親身經歷解決問題的過程，體驗問題解決后的欣喜， 以及收獲發現新方法的創造感。

（2）師生繼續深入探索，揭示了“多次重疊”背后的數學原理，提出了兩種圖形操作關系式（分步式和鏈式），進而從數形結合的角度深化了對面積可加性的認識。簡單的一句話“重疊法真的無效嗎”，竟然引發了一節看得見的生長課，收獲了意想不到的驚喜！此外，該課沿著觀察圖形（觀察法）—操作圖形（重疊法）—提煉原理（操作關系式）的步驟進行，由淺入深，循序漸進地將學生的思維引向深處。有了重疊法教學的深刻，就有了后續生長的簡約（數方格法和測量法教學）。

（3）這節課學生不僅收獲了知識和方法，還培養了學生善于思考、勇于探索、敢于質疑的科學精神。傳統課堂上大都是教師講學生聽，長此以往，學生習慣了接受式教育，缺乏質疑和創造精神。這節課突破了學生機械接受的思維模式，形成一種積極主動、敢于挑戰的創造性思維模式。此外，學生在生疑、質疑、解疑等認識活動中，意識到自己不僅是教材的使用者，還能成為教材建設的參與者和創造者。