基于定位概率和收縮機制的電力系統拓撲演化模型

孫 珂，王 丹，葛賢軍，汪惟源，孫文濤

（1.國網經濟技術研究院有限公司，北京 102209；2.電力系統及發電設備控制和仿真國家重點實驗室（清華大學電機系），北京 100084；3.國網江蘇省電力有限公司，南京 210019；4.國網江蘇省電力有限公司經濟技術研究院，南京 210008）

隨著可再生能源、綜合能源和能源互聯網的快速發展和接入電網，泛在電力物聯網、數字電網時代正在成為可能。傳統的電力系統網絡結構和運行方式已發生了非常大的變化，源-網-荷-儲等多類型參數不確定性越來越多，電網的運行特性和動態行為特征更為復雜，系統運行狀態分析和控制難度大大增加，尤其是電力系統拓撲結構的動態性變強，值得深入研究。

為有效實現對復雜電網拓撲結構的定量分析，通常的做法是：首先，對電力系統的電壓、電流等物理原理進行定性分析；然后結合電力系統母線、變壓器、線路、開關、斷路器等各類型器件的運行特性和彼此的關聯關系，以頻率和電壓穩定為基礎，構建擬分析電力系統網絡的動態數學模型，并設定邊界條件后應用數學求解算法進行仿真分析；最后實現電力系統各個組成元件之間關系定量描述，完成拓撲結構分析。然而，當前以上方法不再完全適用，其主要原因是：①電力系統網絡結構具有動態性，即網絡中的分布式電源、微電網、綜合能源系統等電源，電動汽車、儲能等柔性負荷，以及它們之間的連接是動態的，從而導致電力系統的網絡方程或者數學模型也隨之動態；②具有電源和負荷雙重特性的電動汽車、儲能、微電網、綜合能源系統等元件或子系統規模化接入電力系統，電源和負荷之間的變換成為常態，電力系統網絡建模面臨多源-多網-多荷的動態運行挑戰；③根據電力系統實際運行情況，所構建的網絡動態數學模型極其龐大、維度高，對其計算分析的難度相當高，而且對計算精度和速度等性能的要求也極高，難以滿足實時要求；④為滿足電力系統運行實時性需求，在電力系統建模過程中，通常會對電力系統網絡結構中的部分元件或者子系統進行一些等值簡化，從而降低了結果精度，無法全面體現系統的運行特性；因此，建立一種合理有效的電網動態模型，實現對它的動態特性進行分析，非常必要。

在電力系統拓撲分析建模方面，國內外專家和學者們基于復雜網絡理論[1-10]提出了一些分析模型，主要包括NW（Newman-Watts）隨機網絡模型、WS（Watts-Strogatz）小世界模型、無標度網絡模型等。另外，一些學者也通過復雜網絡理論來尋找電網拓撲結構的薄弱點，從而實現對電力系統的魯棒性和脆弱性分析，以及探索可能存在的大規模斷電故障、系統奔潰等問題[11-19]，其核心目標是保證電力系統的可靠、安全、經濟、穩定運行。但是整體而言，目前基于復雜網絡理論的算法和模型，主要聚焦于系統的“生長”過程，較少考慮系統的精確描述，無法較好從電力系統的規劃設計、網架堅強性提升、故障精準預測與恢復等方面，實現對電力系統網絡宏觀特性的定量分析；當電力系統運行過程中由于故障、經濟調度等導致拓撲結構發生變化時，現有的分析模型已經較難實現有效分析，有些模型甚至出現錯誤結果。

1 電網拓撲動態演化建模

電力系統中含有分布式電源和可再生能源、電動汽車等多類型用戶負荷和鉛酸、鋰電等不同類型儲能等，這些新型源-荷-儲元素在實際運行過程中并網或者離網具有實時動態性，使得對電力系統中任意節點的拓撲變化進行準確地定量分析難度大。為有效實現電網的資源優化配置和運行效率提升，本文擬采用“位置鏈接概率”來分析電力系統網絡拓撲的初始模型，下面進行詳細闡述。

1.1 位置連接概率

為對任意兩個節點之間的位連接概率進行表征，先設定歐式問題空間中任意的兩個節點i和j，它們的坐標分別為(xi,yi)和(xj,yj)，則該兩點之間的歐氏距離為

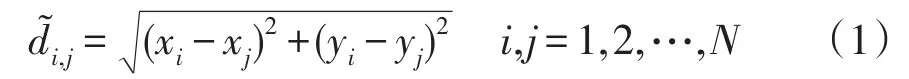
式中，N為網絡中節點的總個數。

同時，設定歐式網絡空間中任意兩個節點之間的最大歐氏空間距離，如式（2）所示。

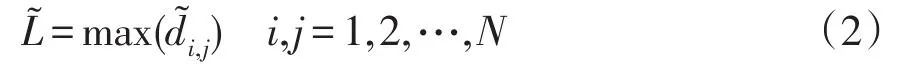
歐式網絡空間中任意兩個節點i和j之間的位置鏈接概率p（i，j）為

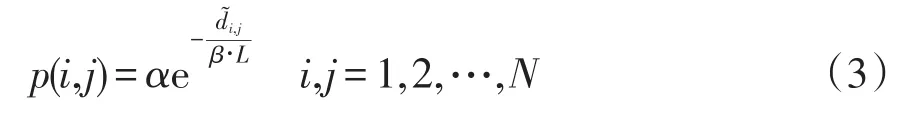
式中，α、β是取值范圍為(0,1]的調節參數。

電力系統拓撲結構發生變化實現動態演化，拓撲結構中的任意一個節點連接關系變化具有以下常識：①電源、負荷及網絡中任意的一個節點都會根據自身運行的不同需求進行并網、離網等重構工作；②依據電力系統動態運行特點，新的電源或者負荷節點加入網絡拓撲，具有隨機性；③網絡中的任意一個節點均可能隨時由于故障原因，實時斷開與它連接的所有節點，自身形成孤島運行。因此，以概率p1、p2和p3分別表示電力系統網絡拓撲結構中增加節點、重連節點、斷開和孤立節點等三種重構行為，并且p、p2和p3需滿足式（4）、（5）的約束。

其中，式（5）確保了電力系統網絡結構中總節點數目為增長的趨向，從而可確保電力系統網絡不會隨著演化的過程解裂為離散點，導致無法構成正常運行的網絡，式（5）的約束也正好反映了真實的電網在演化過程中可一直保持電網的動態穩定平衡。

1.2 電力系統動態演化模型

在實現對電力系統任意節點連接概率定量表征的基礎上，為有效分析電力系統拓撲結構中所有節點的推演變化，設計了電力系統拓撲結構的收縮機制推演模型，實現的主要步驟如下：

（1）初始化網絡。首先，構建出擁有Nstart個節點和M條邊的初始網絡，而且節點之間的連接概率應該滿足式（3），且電力系統網絡的邊數M應滿足

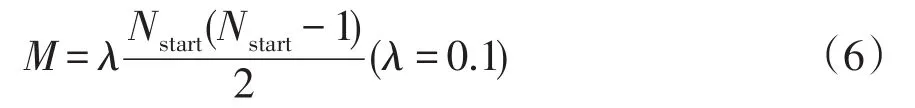
（2）新增節點。以概率p1新添一個電力系統網絡拓撲節點，且該節點與原來已存在的節點彼此連接，并形成m1條邊；

（3）重連節點。以概率p2隨機挑選電力系統網絡中原有一些節點的m2條邊，讓這m2條邊與其他節點發生隨機的重連操作；

（4）刪除節點。以概率p3隨機刪掉電力系統網絡中的任意一個節點，且刪除與該節點相連的所有邊；

（5）終止操作。在每一次的操作過程中，以概率p1、p2和p3，挑選以上（2）、（3）、（4）中的任意一個步驟來執行操作，并一直進行收縮循環執行，直到所操作的次數達到電力系統網絡拓撲中的節點個數預先設定值Nend為止。

按照以上基于收縮機制的電力系統動態演化模型步驟，設定位置連接概率的調節參數α,β初始值分別為0.1和0.3，總節點數為Nstart=20，分析節點為20的初始電力系統網絡結構的推演過程，其結果如圖1所示。

依次類推，按照電力系統動態演化規律的步驟，分別對終止節點總數的IEEE 57、118和300的三種電力系統網絡結構進行推演，其結果如圖2所示。

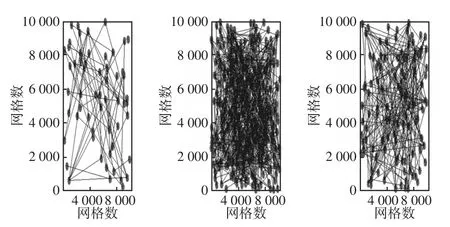
圖2 IEEE 57、118和300節點網絡模型演化結果Fig.2 Evolution results of IEEE 57，118，and 300 node network models

2 動態演化模型拓撲特性分析

圖1和圖2的結果，可以一定程度上說明電力系統的拓撲結構整體節點總數的基本演化過程，但無法完成網絡內部任意一個節點變化情況描述，缺乏有效的定量分析指標。為此，為有效衡量動態演化模型的量化特征，提出相關的評價指標，主要包括平均路徑長度、聚類系數、節點度和網絡的度分布等4個指標。

（1）平均路徑長度L為

式中：di,j為系統網絡拓撲中任意兩個節點為i和j之間的距離；N是電力系統網絡拓撲的總節點數。

（2）設電力系統網絡拓撲中任意一個節點i與ki個節點相連，即節點i擁有ki條邊，則該節點的網絡聚類系數C為

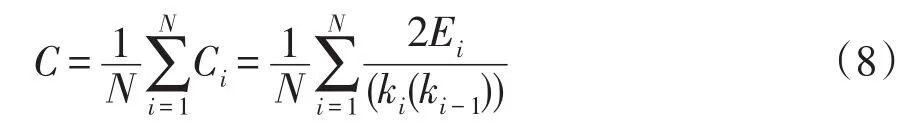
式中：Ei為其他ki個節點它們之間相連接的總邊數；Ci為節點i自身的聚類系數。

（3）設定節點度k是指電力系統中任意節點i擁有邊的條數k；網絡的度分布P(k)是指電力系統任意一個節點其節點度為k的概率。由公式（4）不難發現，整個電力系統網絡拓撲中所有節點度分布的之和應當滿足，其中，Pi(k)表示網絡拓撲中任意節點i的度分布。為此，從常識可知在復雜網絡中，節點度k的值越高，說明該節點與其他節點連接越多，也說明與該節點相連的邊越多。

2.1 節點度分布特性分析

進一步，為了表征本文所提動態演化模型中度分布的時變規律。假設任意時刻t，度分布值為k的電力系統網絡拓撲中任意節點度分布概率為P(k,t)。針對新增節點，設定網絡拓撲中新添加任意一個節點，有且僅有帶入一條邊，由參考文獻[15]可知，該節點的度分布概率Pa(k,t)為

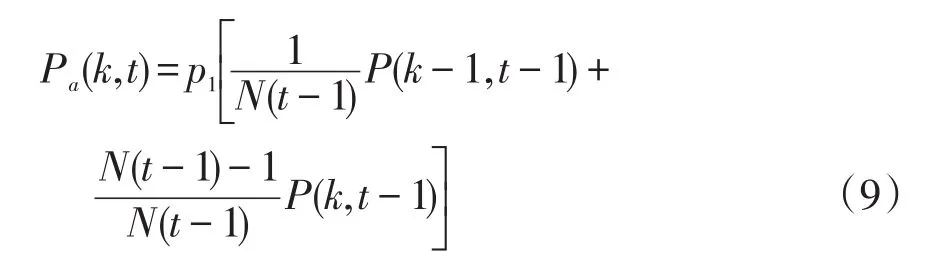
式中：N（t-1）為電力系統網絡中(t-1)時刻節點的總數目；P（k-1，t-1）為電力系統網絡中該節點上一個（t-1）時間的節點度分布概率。

同理類推，針對重連節點，假設任意時刻t，網絡拓撲結構中任意一個節點i的一條邊從節點i與另一個節點j相連，則此時該節點的網絡度分布概率Pr(k,t)為

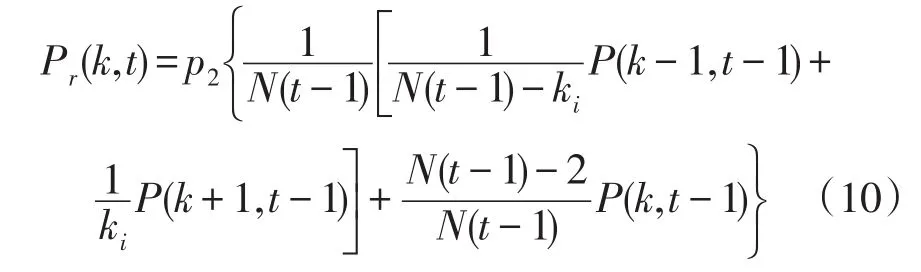
進一步，假設任意時刻t電力網絡中的一個節點i，將與該節點i相連接的所有邊都被刪除，則該節點刪除連接后的網絡度分布概率[15]為

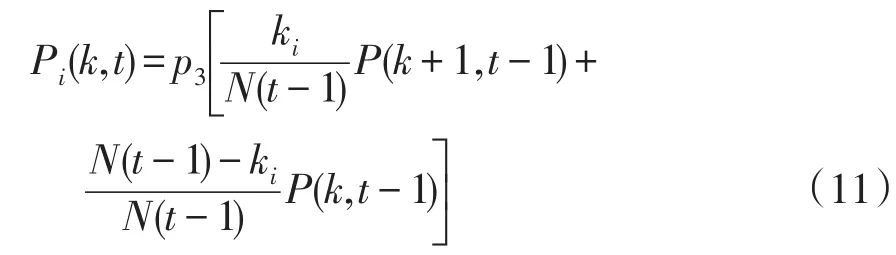
聯合節點連接概率約束方程（4）、（5），任意t時刻，電力系統網絡度分布概率P(k,t)的遞推表達式為

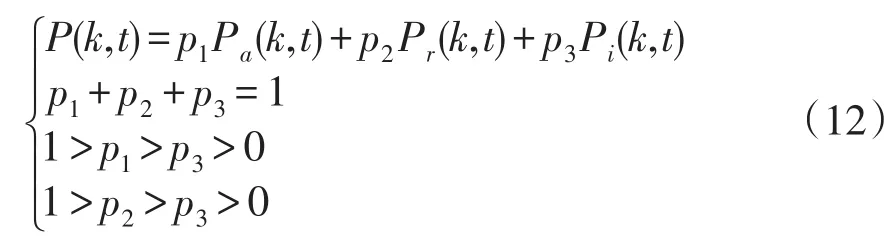
此處需要說明的是，為了確保式（12）的普便適用價值而不失一般性的特征，進行如下約定：①假定任意時刻t內，任意新添的節點i僅僅相應的增加一條邊；②每一個節點i也都僅有一條邊從該節點重新連接到另一個節點j；③一旦電力系統拓撲結構中存在多條邊的變化，可將其視為分多步執行。

根據2.1的原理，分別對IEEE 57、118和300節點進行度分布特性分析，結果如圖3所示。從圖3不難發現，該模型的網絡度分布具有冪律分布的特性，即IEEE三種拓撲結構中均出現某些節點度要比其他節點大得多。這些度分布比較大的節點與網絡中的其他節點連接相對緊密，跟其他節點的能量交換相對比較容易，是網絡拓撲結構中相對“特別重要”的節點；這些節點一旦受到攻擊或者損壞，將可能導致電力系統的奔潰、解裂等，它們對電力系統魯棒性提升、安全性加強等意義重大。

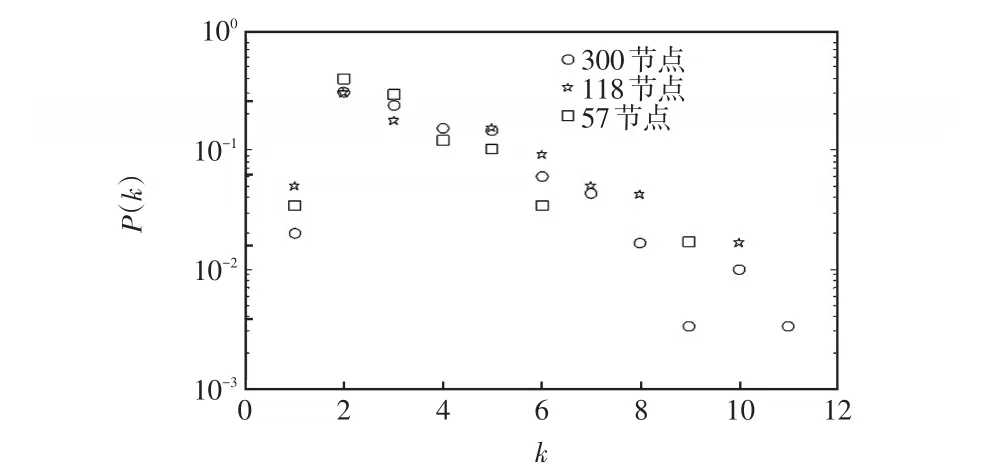
圖3 IEEE 57、118和300節點網絡的度分布情況Fig.3 Degree distribution of IEEE 57，118and 300 node networks

2.2 動態網絡模型評估

為驗證節點連接概率在電力系統拓撲結構推演過程中的作用，選取節點連接概率調節參數α,β為0.1和0.3，分別對IEEE 39、IEEE 57、IEEE 118、IEEE 162和IEEE 300等不同標準測試系統進行分析，其結果數據見表1。從表1中不難發現，通過選取不同的調節參數，不同的標準測試系統具有一定的規律。

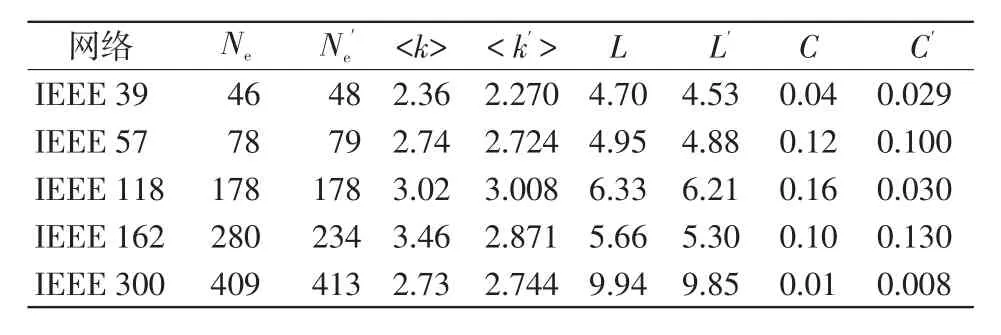
表1 IEEE標準電力系統和本文推演模型評價指標值對比Tab.1 Comparison of evaluation index values between IEEE standard power system and the proposed evolution model

表1中：Ne、＜k＞、L、C分別為IEEE 標準測試系統的網絡總邊數、平均度數、平均路徑長度和網絡聚類系數；、＜k′＞、L′、C′分別本文所提出的推演模型仿真所得的相對應結果。

設定調節參數α和β分別為0.2和0.3，初始網絡節點數為Nstart=20，則IEEE 57、118和300標準系統的網絡聚類系數與網絡節點的總度數如圖4和圖5所示。

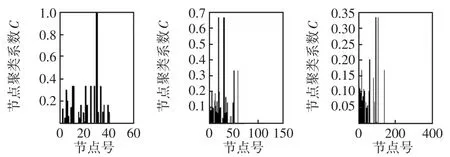
圖4 IEEE 57、118和300網絡節點的聚類系數Fig.4 Clustering coefficients of IEEE 57，118 and 300 node networks

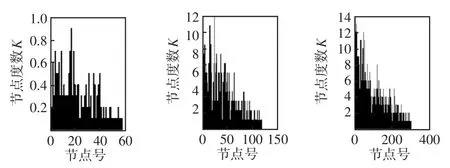
圖5 IEEE 57、118和300網絡節點的節點度數Fig.5 Node degrees of IEEE 57，118 and 300node networks

從圖4不難發現，在三種標準測試算例的網絡拓撲中有一些節點的聚類系數為0，即這樣的節點與其他節點相連的邊數非常少，從而也印證了這樣節點的外部連接非常弱、魯棒性較差，最好不要作為電源節點，特別是當將其作為重要的供電電源節點時，一旦受到攻擊，風險較大。反之，擁有高聚類系數的節點，說明該節點與電力系統網絡中其他節點聯系緊密，當電力系統網絡中此類節點受到攻擊，可以通過與它有密切彼此聯系節點的轉供，實現電網的穩定運行，相對比較適合選作電網的樞紐點，能有效提升系統供電可靠性。當然，當分布式能源出力過大，還可考慮將分布式電源產生的多余能量，利用鉛酸、鋰電池等儲能設備先將它們儲存起來，然后在系統負荷高峰時，進行放電補充電網缺口，從而達到系統可靠供電。

同理，在圖5中，也存在一些節點的度分布值比較高，這些度分布值較高的節點也是其電力系統網絡運行中的“重要節點”，從系統穩定運行角度出發，可選作為主要供電電源或重要用電負荷的安放點。

2.3 模型可靠性分析

電力系統運行過程中故障、運行調度等將會使一些節點與系統解列，即刪除節點。為此，為分析在電力系統網絡拓撲動態演化過程中，概率p3刪除節點變化對電力系統網絡拓撲的運行特性的影響大小，下面詳細闡述。

依然以IEEE 57、IEEE118、IEEE162和IEEE300節點標準測試系統為例，圖6、7、8、9分別是IEEE 57、118、162和300標準測試系統的總邊數、網絡平均路徑長度、網絡聚類系數及總節點度數等4個指標的變化趨勢曲線，按照概率p3刪除節點，分析其變化趨勢。

從圖6～圖9，不難發現：

（1）由圖6知，刪除概率p3值越大，電力系統網絡拓撲的總邊數就越少；反之，如果刪除概率p3值越小，電力系統網絡拓撲的總邊數相對較多，刪掉電力系統網絡中的節點對其影響相對較小。

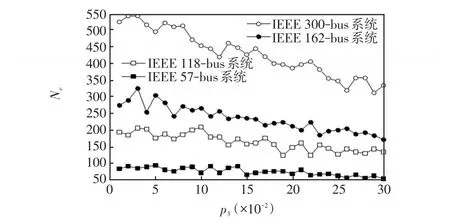
圖6 IEEE標準測試算例的網絡總邊數隨p3變化情況Fig.6 Changes in the total number of edges in IEEE standard test example withp3

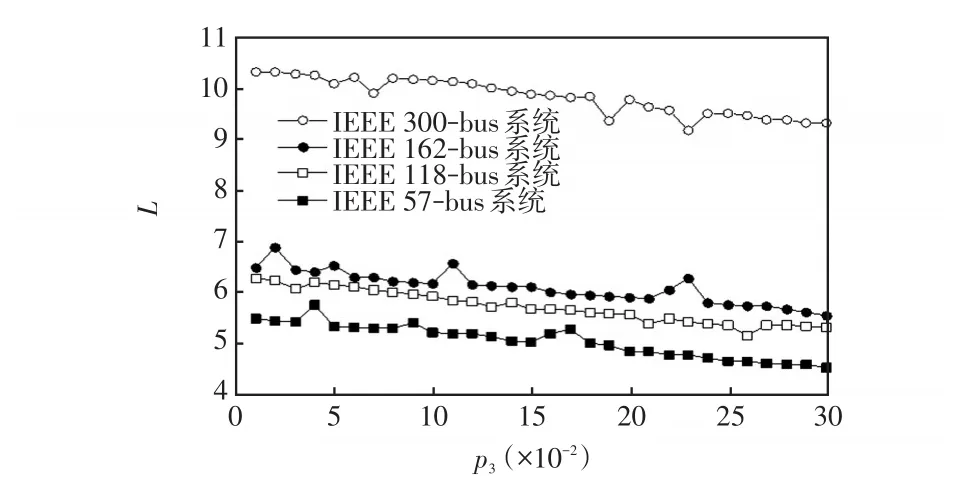
圖7 IEEE標準測試算例的平均路徑長度隨p3變化情況Fig.7 Changes in average path length of IEEE standard test example withp3

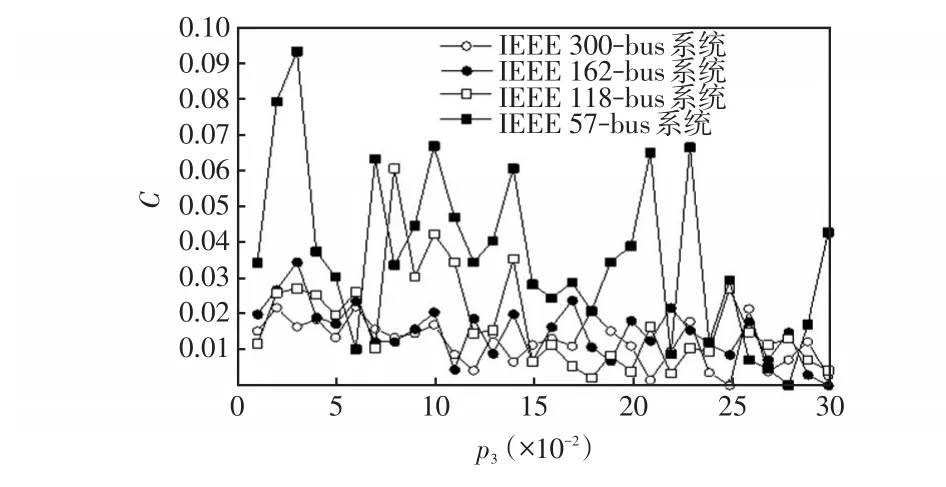
圖8 IEEE標準測試算例的聚類系數隨p3變化情況Fig.8 Changes in clustering coefficient of IEEE standard test example withp3

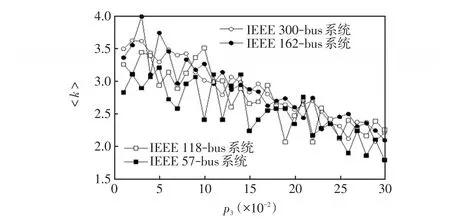
圖9 IEEE標準測試算例的總節點度數隨p3變化情況Fig.9 Changes in total node degree of IEEE standard test example withp3

（2）從圖6還可知，網絡拓撲節點數越多，它的斜率比節點數少電力系統網絡的斜率要大，其主要原因是最終節點數多的網絡，它的每一個節點會與電力系統網絡中的節點有相對較多的相連，從而會得到更大的度分布值。說明刪除節點對網絡拓撲影響大。

（3）從圖7可知，刪除節點的概率p3值越大，網絡中平均路徑長度越短，但其曲線的波動范圍相對較小，表明網絡中刪除節點，對節點之間的最短路徑距離影響相對小。

（4）從圖8可知，概率p3的刪除節點變化對電力系統網絡聚類系數的影響并無明顯規律，是一種毫無明顯特征的波動曲線，僅僅呈現一定的波動規律，即電力系統網絡節點越多，其曲線波動相對較小，因此說明：節點總數較大的電力系統拓撲結構相對比較復雜，此時一些節點的刪除或者退出運行對網絡拓撲中節點之間的交叉聯系影響不大，也印證了電力系統網絡越復雜，一旦節點失電，實現對該節點的轉供電概率相對越高。

進一步，近年來國內外的專家和學者們通過大量的仿真實驗還發現，節點刪除概率p3值不能無限擴大至1（全部刪掉，系統停運），其上限應小于0.32，即p3＜0.32，一旦刪除節點概率值大于0.32，網絡解裂的速度就會大于連接的速度，將會導致整個網絡崩潰，此時無論電力系統網絡結構多復雜，其最終結果將是系統的不穩定，從而也印證了作為剛性特點的電力系統，其穩定是有邊界的。

當然，電力系統在運行過程中一般擁有一定面對多類型故障的承受和自愈能力，即電力系統的魯棒性。進一步，結合現在電力物聯網的特點，下面從系統抗隨機故障、抗主動攻擊等兩個維度，應用本文所提出的電力系統動態演化模型來分析系統的魯棒性。分別模擬系統抗隨機故障和抗主動攻擊兩種故障類型，計算IEEE 57、118和300節點電力系統中受影響節點數量，其曲線如圖10所示。

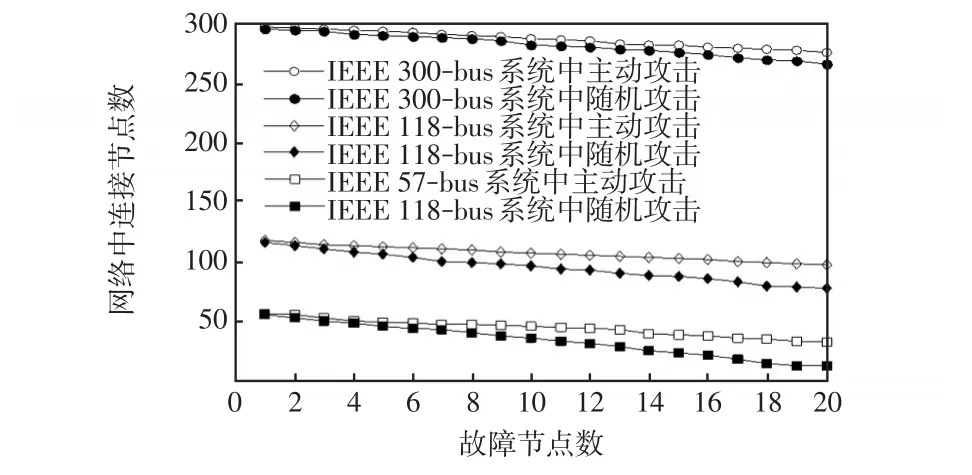
圖10 隨機故障與主動攻擊對IEEE標準測試系統節點的影響Fig.10 Effects of random failures and active attacks on nodes of IEEE standard test systems

從圖10不難發現。

（1）主動攻擊的對象選取最大度數的電力系統網絡節點為最佳，一旦此類電力系統節點受到攻擊，與其連接的節點變為刪除節點，系統的整體魯棒性大大降低。因此，在實際電力系統主網架結構搭建過程中，在這些關鍵網絡節點上配置冗余和保護機制，可有效提升系統可靠性。

（2）隨機故障與主動攻擊相比，系統的魯棒性更強。其主要原因是隨機故障具有強突發性，故障點大概率發生在一些非重要節點，此時對電力系統的影響有限。這也印證了電力系統具有一定的彈性。

（3）隨著IEEE 57、IEEE118和IEEE300節點總數增多，其網絡系統的魯棒性會相應的增強，這與2.3節中刪除節點對電力系統影響的作用所獲得的結論基本一致，從而也印證了互聯互通的復雜電力系統穩定性更強。

（4）在電力系統主網架結構的規劃和設計階段，應盡可能減少對個別重要節點的依賴作用，通過增加節點之間的互聯互通，形成電力系統多個樞紐節點共存態勢，實現電力系統可靠性提升。

（5）本文所提模型可定量分析電力系統網絡拓撲節點對可靠性的作用。根據計算結果對關鍵節點安裝設備和加強保護，實現電網整體運行的安全性提升，并節約了投資建設成本。

3 結語

本文提出了一種基于定位概率和收縮機制的的新型網絡建模方法，通過采用復雜網絡度量來評估和揭示電力系統網絡拓撲的關鍵統計學特性。所提出的動態演化建模方法可從拓撲角度對電力系統的演化特征和復雜動態行為進行分析。此外，所提出的網絡模型，也可以對電網的系統魯棒性和脆弱性進行系統化的評價和分析。

著眼未來，電力系統網絡拓撲推演模型可著重從以下兩個方面進行開展深入研究：一方面是基于真實的電力系統運行狀態對所提出的模型進行驗證和分析；另一方面，可將電網的可靠性分析和級聯故障傳播機制納入所提出的模型，從而有效提升電網絡規劃的有效性和運行的可靠性。