變壁厚渦旋膨脹機型線參數的優化分析

彭 斌, 蔣 龍

(蘭州理工大學 機電工程學院,甘肅 蘭州 730050)

0 引 言

渦旋機械以其良好的結構特性和力學特性被廣泛地應用于制冷、增壓機、渦旋泵等領域。對渦旋機械的研究可以追溯到19世紀末,并且一直在不斷地發展進步。現階段,根據所用領域的尺寸要求和性能要求的不同,渦旋機械依舊在不斷地改進當中。

作為渦旋機械的核心,渦旋型線的設計優化是渦旋機械設計研究的重點,因此國內外眾多學者對其進行了廣泛深入的研究。

在圓漸開線渦旋型線的幾何參數研究方面:文獻[1]提出等效缸徑的概念,把型線高度、齒寬、壁厚化為3個獨立準則數;文獻[2]提出了一種摩擦功耗和泄漏損耗較小的幾何參數設計方法;文獻[3]對比分析了渦旋型線幾何參數和結構參數之間的關系,并計算了動渦旋盤所受的氣體力;文獻[4]提出了一種用于容積分析描述的新型渦旋壓縮機幾何模型;文獻[5]分析了渦旋壓縮機的幾何和動態特性,研究了幾何連續性對渦旋壓縮機性能的影響;文獻[6]、文獻[7]分別對幾何模型進行了優化分析。

通過上述文獻可以看出，對圓漸開線渦旋型線幾何模型的研究主要以泄漏、氣體力、動態特性等為目標,為變壁厚渦旋型線的研究方向提供了參考。

在變截面渦旋型線幾何參數研究方面:文獻[8]研究了多種漸開線的性能特點,提出了渦旋型線嚙合的計算方法;文獻[9]研究了采用三點弧近似法對變壁厚渦旋的加工;文獻[10]提出了基于泛函理論的變壁厚渦旋型線設計理論及其優化設計方法,建立了變壁厚渦旋型線優化數學模型;文獻[11]提出了包括漸開線等微分條件、基于復合網格劃分誤差和渦旋型線的嚙合間隙來定義型線的誤差靈敏度;文獻[12]提出了利用橢圓漸開線和雙包絡法設計渦旋型線,并進行了建模分析;文獻[13]建立了多種齒頭修正后的幾何模型,通過定義的幾何參數對吸氣容積進行了計算;文獻[14]提出了雙圓弧加直線單元組合型線,推導了該組合型線的工作腔容積,研究其變化規律。

目前,關于變壁厚渦旋型線的研究主要集中在變壁厚渦旋型線幾何模型的問題、數學模型的構建以及相關模型的模擬上，而關于幾何模型中各參數對型線的影響和對幾何模型的優化分析涉及較少。

本文從變壁厚渦旋膨脹機的幾何特性出發,以渦旋型線占積比(即型線面積所占盤的面積比)為優化模型,對圓漸開線、圓漸開線-高次曲線-圓漸開線、圓漸開線-圓弧-圓漸開線3種型線進行對比分析,并運用遺傳算法分別對高次曲線、圓弧組合型線的參數選取進行了優化,為今后變壁厚渦旋膨脹機的設計提供一定的參考。

組合型線示意圖如圖1所示。

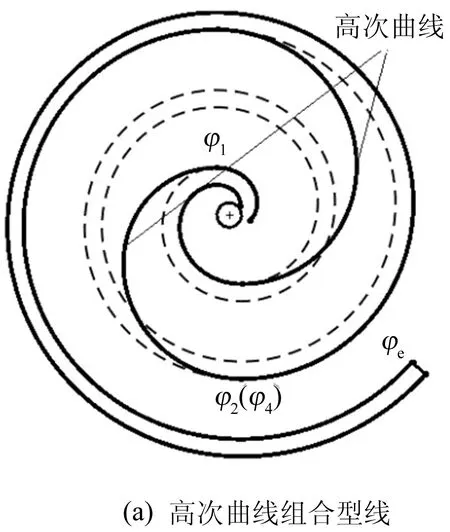
圖1 組合型線示意圖

1 渦旋型線的方程

1.1 圓漸開線-高次曲線-圓漸開線

圓漸開線-高次曲線-圓漸開線組合型線的齒的開始部分與結束部分為圓漸開線,中間連接段為冪級數形式的高次曲線,其中齒頭采用雙圓弧加直線修正,如圖1a所示,其公式[15]描述如下。

圓漸開線母線公式為:

(1)

其中:φ∈(0,φ1)∪(φ2,φ3);φ為型線的展角;Rg=a;Rs=aφ，a為基圓半徑。

高次曲線母線公式為:

(2)

其中

φ∈(φ1,φ4);

Rg2=c1+2c2(φ-π/2)+3c3(φ-π/2)2;

Rs2=c0+c1(φ-π/2)+c2(φ-π/2)2+

c3(φ-π/2)3。

根據渦旋型線的嚙合原理[16]可得:

(3)

1.2 圓漸開線-圓弧-圓漸開線

圓漸開線-圓弧-圓漸開線組合型線與高次曲線的組合曲線類似,只是齒中間段由圓弧替代了圓漸開線,如圖1b所示。但圓弧和嚙合點的確定與高次曲線有很大差別,圓弧欲滿足嚙合要求和連續性要求,需滿足一個必要條件,即

λ/2+nπ=tan(λ/2)

(4)

其中:λ為圓弧中心角;n為圓漸開線被代替的圈數。

圓漸開線的母線與高次曲線組合型線相同,不再贅述,圓弧的相關參數確定如下所述。

靜盤外壁圓弧中心O2的坐標為:

(5)

靜盤內壁圓弧中心O1的坐標為:

(6)

靜盤內、外壁圓弧半徑R、r為:

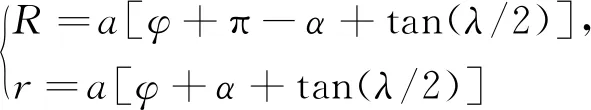
(7)

其中:a為基圓半徑;α為漸開線發生角;φ為連接處初始展角。

1.3 渦旋型線的占積比

圓漸開線渦旋型線在基圓一定、最終展角一定的情況下,型線的面積是定值,因此無法進行優化選擇,組合型線則能很好地改善這一狀況。對于組合型線的面積計算,可以以各連接段的接點為求解范圍,分別求出各段面積后進行相加求得,但這樣的計算分段過多,且內、外壁型線的類型存在不相同的情況,導致計算相對復雜。

本文提出一種新的幾何模型-渦旋型線占積比,即渦旋型線占有效盤面積的比值。由于在漸開線初始條件一定的情況下,無論是高次曲線組合型線還是圓弧組合型線,其最終嚙合所需直徑都與圓漸開線相同,在這種情況下,渦旋型線面積越小即占積比越小,有效容積越大。因此討論占積比可以間接反映各組合型線的膨脹性能。

首先整體求解外壁型線面積和內壁型線面積;然后用外壁型線面積減去內壁型線面積的方法,進行型線面積的計算。

(8)

(9)

(10)

雙圓弧加直線修正面積[17]為:

Sx=0.5(R2-r2)(τ-sinτ)

(11)

其中:τ=0.5π-γ-θ,γ為修正角,θ為連接點展開角;R為大圓弧半徑;r為小圓弧半徑。

內、外壁弧長示意圖如圖2所示。

圖2 內、外壁弧長示意圖

可得內、外弧線所圍成的面積Sn、Sw和渦旋型線的面積S為:

(12)

(13)

Sw=So+Sg

(14)

Sn=So+Sw+Sx

(15)

S=Sw-Sn

(16)

(2) 圓漸開線-圓弧-圓漸開線組合型線。該組合型線中,圓漸開線型線所圍成的面積的計算與高次曲線組合型線相同,圓弧的內、外面積Sn、Sw和渦旋型線面積S計算如下:

(17)

(18)

S=Sw-Sn

(19)

(3) 型線占積比模型的建立。型線的占積比就是型線面積與有效盤面積的比值。其中,動靜渦旋嚙合后,動渦旋以回轉半徑Ror為運動半徑進行公轉平動,有效盤面積取最終展角時弧線半徑加Ror為半徑進行計算,即

rp=a(Be-A)+Ror,

(20)

根據(16)式、(19)式可得型線的占積比為:

(21)

2 各參數的影響分析

由(8)～(21)式可知,高次曲線組合型線和圓弧組合型線的型線面積都與基圓半徑a、回轉半徑Ror、最終展角φe有關,運用控制變量法研究以上各參數對占積比的影響。

2.1 基圓半徑對占積比的影響

基圓半徑對型線面積和占積比的影響如圖3所示,其中基圓半徑從3 mm增加至5 mm,回轉半徑與最終展角保持不變。從圖3可以看出:在相同基圓半徑下,圓漸開線的型線面積遠遠大于組合型線的型線面積,而高次曲線組合型線的型線面積略低于圓弧組合型線的型線面積;圓漸開線的占積比約為其他2種組合型線占積比的2倍,高次曲線組合型線的占積比略低于圓弧組合型線的占積比。

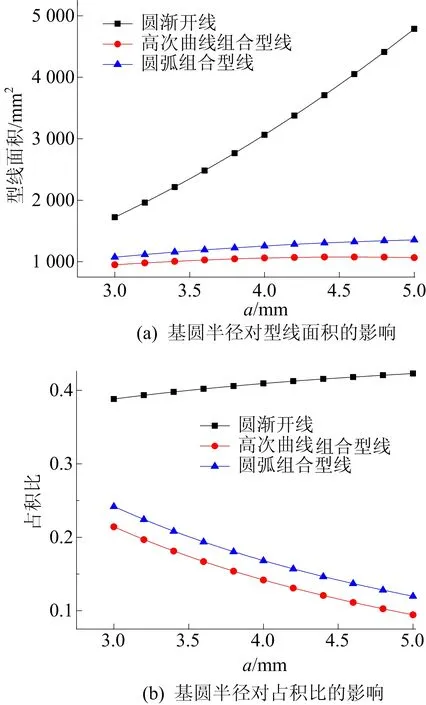
圖3 基圓半徑對型線面積和占積比的影響

由圖3可知：隨著基圓半徑的不斷增加,圓漸開線的型線面積近乎于直線上升,其型線占積比也有所升高,這是因為隨著基圓半徑的增加,型線的齒厚增加,導致型線面積大幅度增長,所以型線占積比也變大;其余2種組合型線的型線面積有小幅度增長,而型線占積比卻有所下降,這是因為當基圓半徑增加時,高次曲線與圓弧的弧長增長幅度很小,而圓漸開線部分齒厚雖然有所增長,但節距也隨之增加,在回轉半徑和最終展角保持不變的情況下,有效盤面積中的圓漸開線面積減小,所以占積比有所下降。

從圖3b還可以看出，在基圓半徑、回轉半徑、最終展角相同時,高次曲線組合型線和圓弧組合型線的占積比相差不多,且都要優于圓漸開線的占積比。

2.2 最終展角對渦旋型線的影響

最終展角對渦旋型線的影響如圖4所示,其中最終展角由12.56 rad增加至18.06 rad,基圓半徑和回轉半徑保持不變。

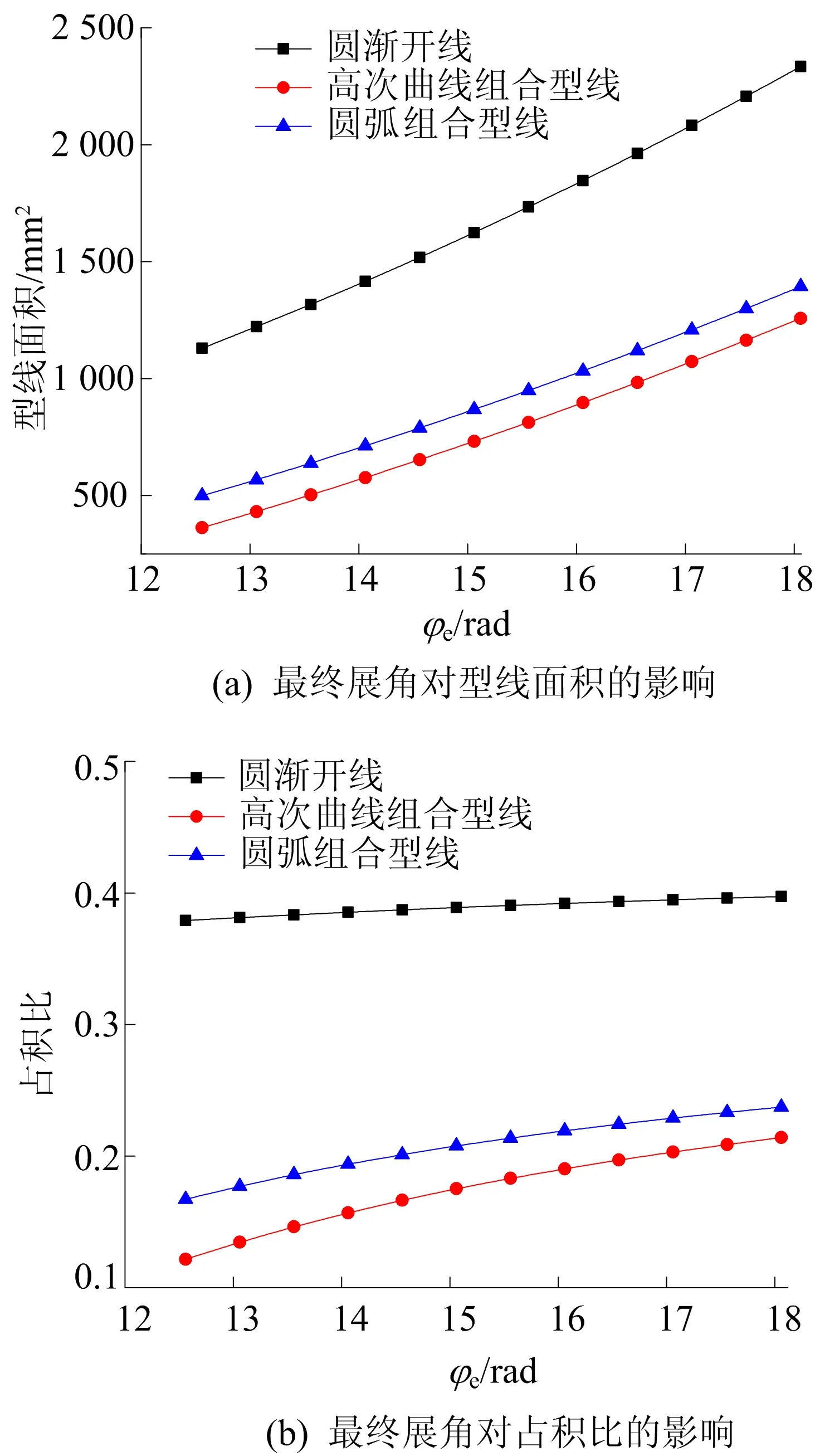
圖4 最終展角對型線面積和占積比的影響

從圖4可以看出:當最終展角增加時,圓漸開線、高次曲線組合型線、圓弧組合型線的型線面積都有明顯的增加,且趨勢也近似;但圓漸開線的占積比幾乎沒有增加,這是因為當最終展角增加時,型線齒厚增加,面積增加,同時有效盤面積也增加,且增長率近似,所以占積比沒有明顯增加;而高次曲線組合型線和圓弧組合型線的占積比有所增加,這是因為當最終展角增加時,高次曲線部分和圓弧部分皆無變化,但圓漸開線部分弧線增加,即圓漸開線型線面積所占比例增加,所以占積比有所增加。

從上述對基圓半徑、最終展角的分析可知:在相同條件下,高次曲線組合型線和圓弧組合型線的型線面積、占積比都遠遠小于圓漸開線;而2種組合型線相差不大,且變化趨勢相近。

3 高次曲線組合型線參數的優化選取

3.1 遺傳算法理論

遺傳算法是運用仿生學中基因的遺傳、變異等原理,將已知邊界條件的優化參數看作一段“基因”,通過選擇保存每一代的最小值,經過一定概率的重組變異,產生新的一代“基因”,如此循環,直至達到預設目標或者遺傳代數達到預設而終止。

遺傳算法流程如圖5所示。

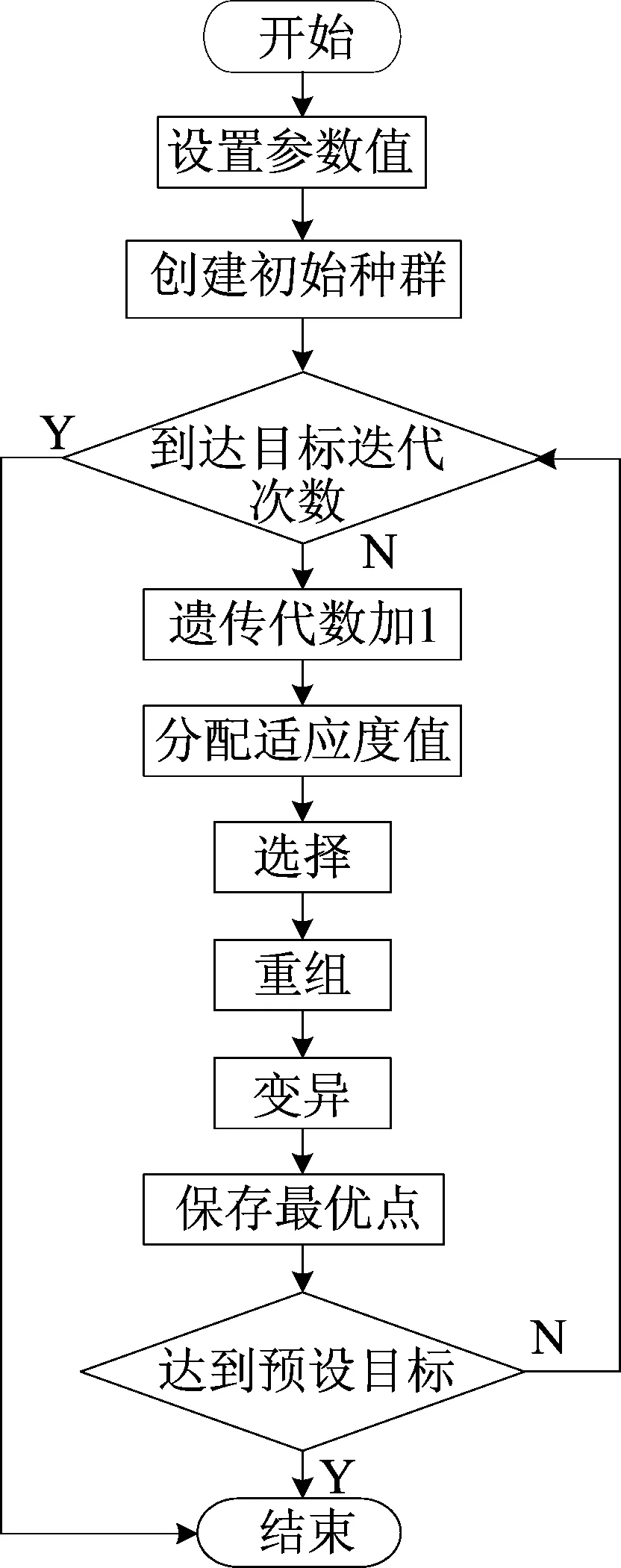
圖5 遺傳算法流程

本文主要以型線面積S和占積比δ為優化目標,其求解方式為(16)式、(19)式和(21)式。由型線面積的定義可知,S>0且S?Sp;由占積比定義可知,0<δ<1。

3.2 連接點處展角優化選取

本文以φ1、φ4為優化變量,即2對“基因”,以高次曲線的占積比為目標函數進行優化分析。參數選取為:基圓半徑a=3.2 mm;回轉半徑Ror=5.58 mm;發生角α=2π/9;最終展角φe=16.547 8;圓漸開線展角φ2滿足φ2=φ4+2π。

高次曲線占積比優化如圖6所示。通過50代的“基因”優化,得到最優解δ=0.169 332,此時φ1=2.094 0、φ4=6.283 2。

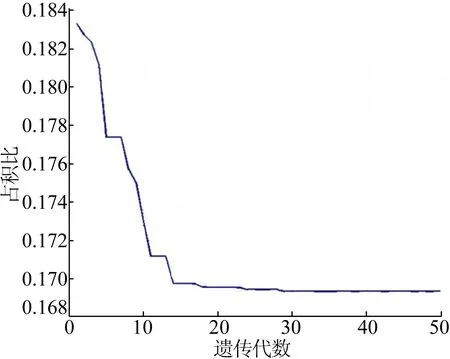
圖6 高次曲線占積比優化

從圖6可以看出,在基圓半徑、漸開線起始角、最終展角等參數不變的前提下,隨著φ1、φ4的變化,組合型線高次曲線部分的弧長發生了變化,從而對組合型線高次曲線的占積比產生了一定的影響。

因此,合理選取φ1、φ4對高次曲線組合型線的占積比有一定的優化作用。

3.3 多初始參數優化

初始參數基圓半徑a和最終展角φe同時變化時,以占積比δ為優化目標,尋求δ的極小值及取極值時各初始參數的取值,結果如圖7所示。

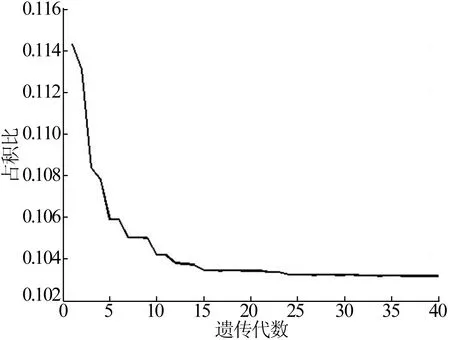
圖7 單目標優化時高次曲線組合型線的多初始參數優化

由圖7可知,在優化了約30代后,占積比取得了極小值,之后保持不變，最終取得極小值δ=0.103 180,此時的基圓半徑a=5.2 mm、最終展角φe=18.84 rad。

3.4 多優化目標下基圓半徑的優化選取

根據上節對高次曲線-圓漸開線組合型線的型線面積S和占積比δ隨基圓半徑a變化的討論可知，型線面積隨基圓半徑的增大而增大,而占積比隨著基圓半徑的增大而減小。下面討論以型線面積和占積比為共同優化目標下的基圓半徑取值。

多優化目標時高次曲線組合型線的多初始參數優化如圖8所示。

由圖8可知,由于2個優化目標隨基圓半徑的變化趨勢相反,無法求出極值。圖8中每個點都是滿足非劣條件下的基圓半徑的取值,將其中值摘選部分,見表1所列。

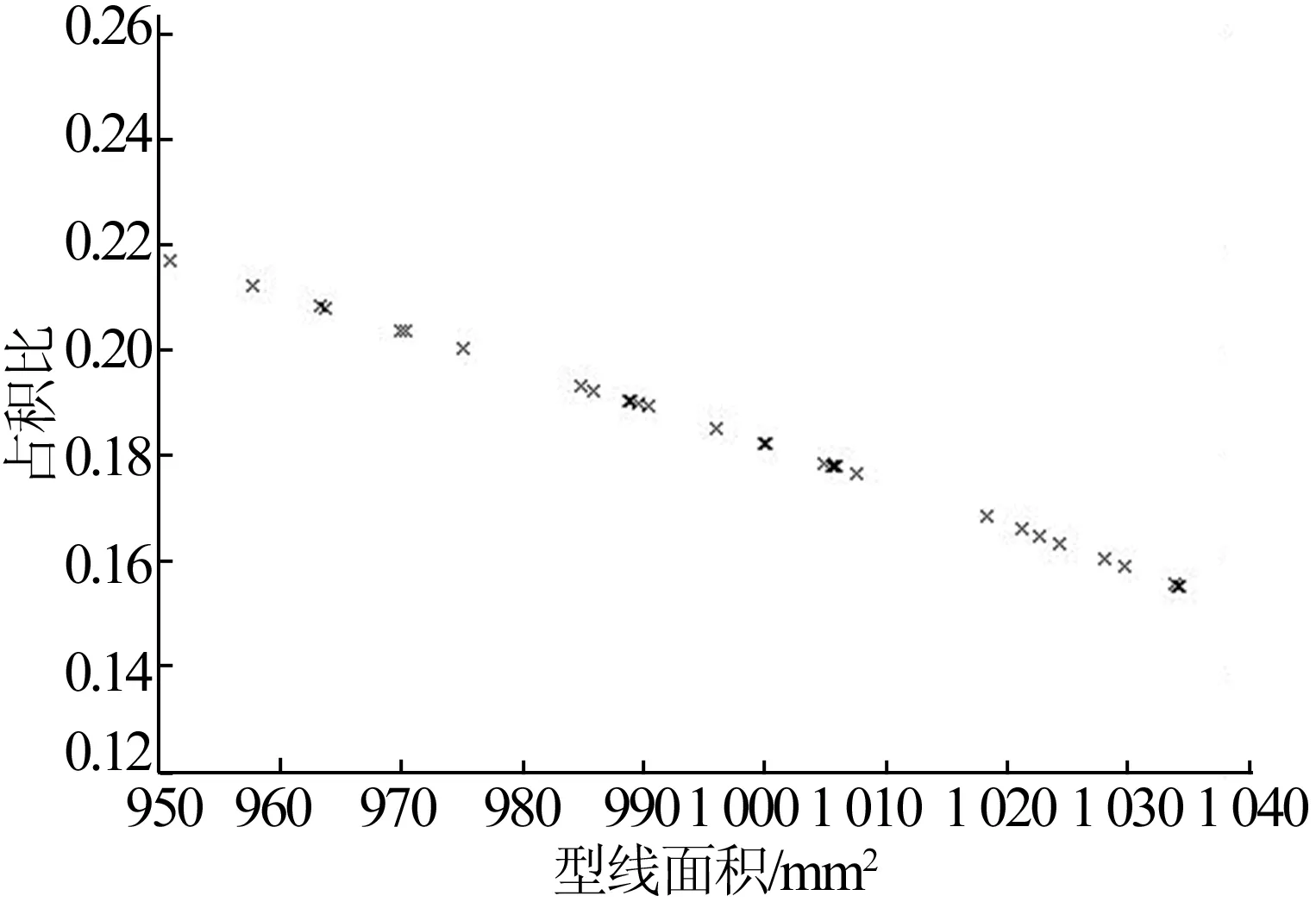
圖8 多優化目標時高次曲線組合型線的多初始參數優化

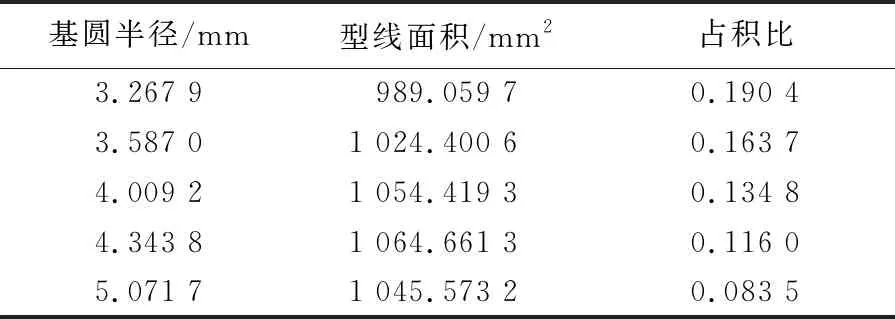
表1 多優化目標下高次曲線組合型線基圓半徑的非劣解集

從圖8可以看出,相比于圖7中多個初始參數共同作用時占積比的極值,單個初始參數變化下占積比的極小值要小于多初始參數下的極小值,即多個初始參數共同作用時會影響優化目標極值的取值。

4 圓弧組合型線的優化

4.1 以占積比為優化目標的多初始參數優化

初始參數基圓半徑a和最終展角φe同時變化時,以占積比δ為優化目標,尋求其極小值以及取極值時各初始參數的取值,結果如圖9所示。

從圖9可以看出,在最初幾代優化時,占積比迅速減小,在優化10代左右以后,變化相對平穩,在遺傳至40代左右時取得極小值δ=0.139 61,此時的基圓半徑a=3.499 3 mm、最終展角φe=12.56 rad。

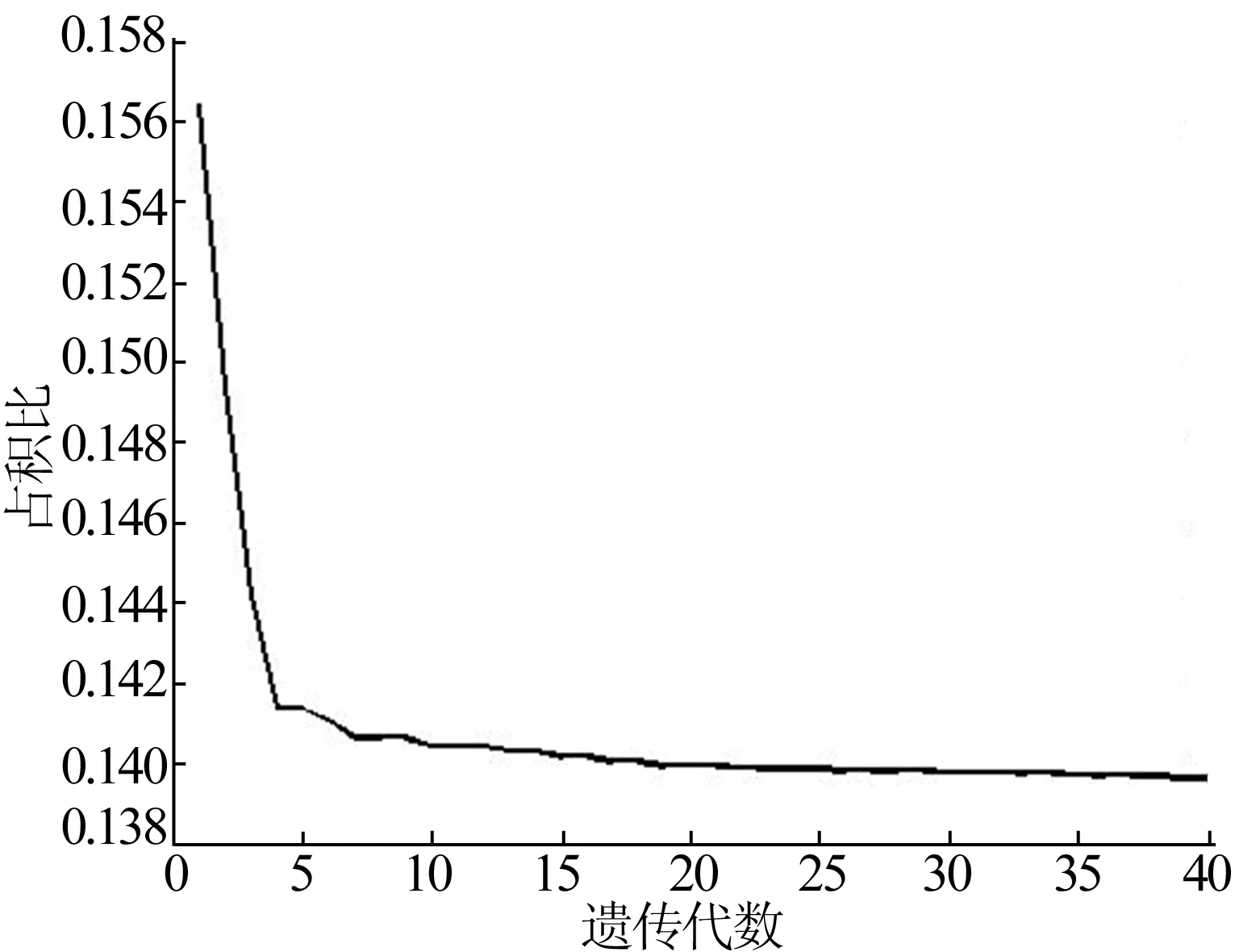
圖9 單目標優化時圓弧組合型線的多初始參數優化

4.2 多優化目標下基圓半徑的優化選取

根據上節對圓弧-圓漸開線組合型線的型線面積S和占積比δ隨基圓半徑a變化的討論可知,圓弧-圓漸開線組合型線的變化趨勢與高次曲線-圓漸開線組合型線的類似。下面討論以型線面積和占積比為共同優化目標下的基圓半徑取值。

多優化目標時圓弧組合型線的多初始參數優化如圖10所示。

由圖10可知:占積比的變化范圍為0.25～ 0.10,型線面積的變化范圍為1 050～1 350 mm;且在基圓半徑取值越大時,占積比的減小率也越大。優化取得一組非劣解集,摘選部分見表2所列。

圖10 多優化目標時圓弧組合型線的多初始參數優化

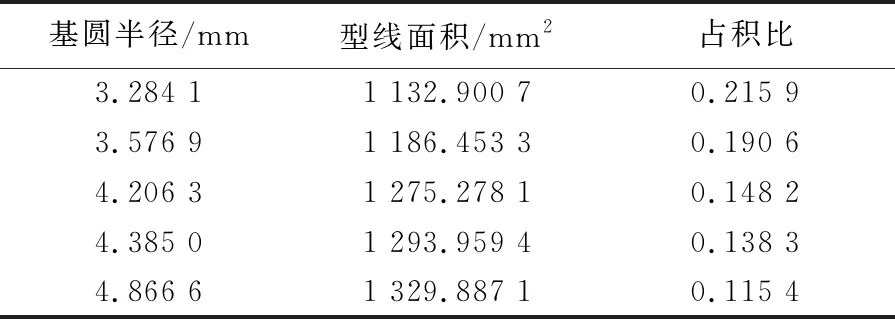
表2 多優化目標下圓弧曲線組合型線基圓半徑的非劣解集

從圖10可以看出,相比于圖9中多個初始參數共同作用時占積比的極值,單個初始參數變化下占積比的極小值要小于多初始參數下的極小值。

5 結 論

本文以高次曲線組合型線和圓弧組合型線為優化對象,以型線面積和占積比為優化目標,運用遺傳算法對其進行了優化分析。

分析得到基圓半徑與型線面積成正比、與占積比成反比,最終展角與型線面積和占積比都成正比。在單目標遺傳算法的優化下得到高次曲線組合型線占積比最優解為δ=0.169 332,此時φ1=2.094 0、φ4=6.283 2;圓弧組合型線最優解為δ=0.139 610,此時基圓半徑a=3.499 3 mm、φe=12.56 rad。以占積比和型線面積為共同優化目標,在多目標遺傳算法的優化下,得到了2個優化目標的一組非劣解集以及與之對應的基圓半徑值。

本文的研究為高次曲線組合型線和圓弧組合型線的參數選取提供了一定的參考。