地震下DMTMD對結構剛度和質量參數攝動的魯棒性

王肖東, 汪 權, 袁加偉

(1.合肥工業大學 土木與水利工程學院,安徽 合肥 230009; 2.陽光城集團,上海 200082)

魯棒性(Robustness)的概念在20世紀60年代提出后,已在系統控制等領域得到廣泛應用。魯棒性指系統在內部不確定性因素影響和外部環境干擾下仍能保持穩定工作的能力。由于在實際的建筑結構振動控制中,建筑結構的模型參數如結構的剛度和質量參數難以用數學模型來精確描述,結構的不確定性會導致系統控制的不穩定和控制性能惡化,為此研究對結構參數和外部擾動具有較好魯棒性[1]。

多重調諧質量阻尼器(multiple tuned mass dampers,MTMD)利用一組頻率分布在結構被控模態頻率周圍的單TMD 控制結構的振動行數值模擬與分析。MTMD是把一個大的TMD分成若干小的TMD。各個小的TMD的頻率以結構被控模態頻率為中心按一定頻帶寬度縱向分布。MTMD有效改善了單個TMD控制效果不穩定、適用激勵頻帶過窄、可實現性較差的特點。MTMD相比TMD有較好的控制魯棒性。文獻[1]研究了結構剛度攝動而質量不攝動與結構質量攝動而剛度不攝動2種情況,并討論了MTMD的有效性變化趨勢；文獻[2]研究了多自由度結構附加MTMD后的頻率響應特性,計算了不同頻譜特性的地震激勵下MTMD系統的時程響應；文獻[3]研究了某人行天橋的MTMD消能減振分析,經過MTMD最優參數選取后的主體結構的振動響應衰減比單個TMD更有效,而且在更寬的頻帶上仍保持有效性；文獻[4]以崖門斜拉橋為算例,分析了MTMD對橋梁顫振控制的有效性和魯棒性,并編制了多模態耦合顫振MTMD控制和參數分析程序。

盡管單調諧質量阻尼器(single tuned mass damper,STMD)及MTMD控制策略發展較為成熟[5-7],但其在實際工程中的應用[8-9]仍是結構振動控制領域的熱點問題。尤其是結構的魯棒性分析,即結構的剛度和質量攝動變化的情況,研究相對較少。

本文MTMD的控制策略分成了沿頂層布置的MTMD控制策略和沿高度分布的分布式多重調諧質量阻尼器(distributed multiple tuned mass dampers,DMTMD)控制策略。采用國際結構振動控制公共平臺中的20層Benchmark鋼結構模型并利用ANSYS分析軟件建立有限元模型。開展MTMD和TMD的結構剛度和質量參數攝動下的控制魯棒性研究,剛度、質量的單一因素變化的情況和剛度、質量同時變化的情況來分析TMD、MTMD和DMTMD的控制魯棒性。并為設計MTMD的參數設計提供參考。

1 Benchmark模型及模態分析

本文選用的Benchmark模型是國際結構振動控制公共平臺第3階段20層抗震非線性鋼框架結構模型,對其研究可以代表對典型中、高層鋼結構建筑的研究,是美國SAC機構于加利福尼亞州真實設計的結構。

(1) Benchmark模型有限元模型。20層抗震Benchmark模型詳細參數見文獻[10]。

選取整個Benchmark結構的南北方向一榀框架(結構的短方向)進行分析，利用ANSYS軟件建立其有限元分析模型。

結構均采用平面桿系模型,梁和柱等框架單元只考慮材料非線性。梁柱單元均采用雙線性隨動強化模型,以2條直線段描述材料的應力-應變關系。通過彈性模量、屈服應力和切線模量定義應力-應變關系,初始為各向同性材料的小應變問題。本模型為鋼結構模型,為金屬材料,符合初始各向同性的小應變問題。

梁柱采用具有拉壓和彎曲性能的平面彈塑性單軸單元即beam23單元進行模擬,實常數中截面類型設置采用通用截面。定義梁單元弾性模型為2.06×1011Pa,屈服強度為248 MPa,切線模量為2.06×109Pa。柱單元弾性模型為2.06×1011Pa,屈服強度為345 MPa,切線模量為2.06×109Pa(模型詳見文獻[10])。單元兩端每個節點都有3個自由度，即沿節點坐標X、Y方向的平動和繞Z軸的轉動。結構中各層梁材料的密度屬性選用每層全部質量的1/6,而每層柱材料的密度屬性則設置得很小。

在控制系統布置中采用combin14單元來模擬TMD阻尼器彈簧單元,采用mass21單元模擬阻尼器質量單元。combin14和mass21的建立都包括了節點和單元的創建以及參數的賦值,對TMD的研究是通過對combin14單元剛度系數和阻尼系數以及mass21的質量系數的賦值來實現對阻尼器參數的調整。

采用有限元分析軟件ANSYS對第3階段20層Benchmark非線性鋼框架結構抗震模型進行建模,整個模型節點個數190,單元個數284,模型如圖1所示。

(2) ANSYS模型與ASCE提出的模型模態分析比較。根據中國建筑抗震規范,模態控制的數量取決于模態質量參與系數達到90%,從ANSYS分析可知,前5階的累計質量分數達98%。通過ASYS的模態分析得到本模型前5階自振頻率與國際ASCE平臺所提出的采用Matlab仿真結果進行對比,可以看出結果基本一致,見表1所列。

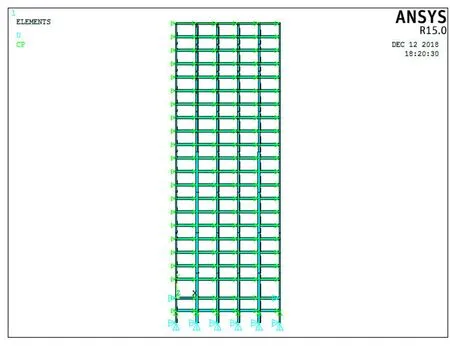
圖1 ANSYS有限元模型

表1 模型結構的固有頻率對比 Hz

2 控制策略設計與評價指標

2.1 控制策略設計

從ANSYS分析可知,前5階的累計質量分數達98%,故取前5階進行DMTMD的設計。在進行DMTMD設計時,每個TMD按前5階振型振幅最大的位置按高度依次設計。MTMD分5個小TMD安裝到最高層的位置。STMD控制質量比μ=0.05,阻尼比ξ=0.05。對于MTMD和DMTMD控制策略設計,5個小TMD的質量比和阻尼比取值相等,并且5個小TMD的質量和等于STMD單個阻尼器的質量。STMD、MTMD、DMTMD控制策略設計分別如圖2所示。

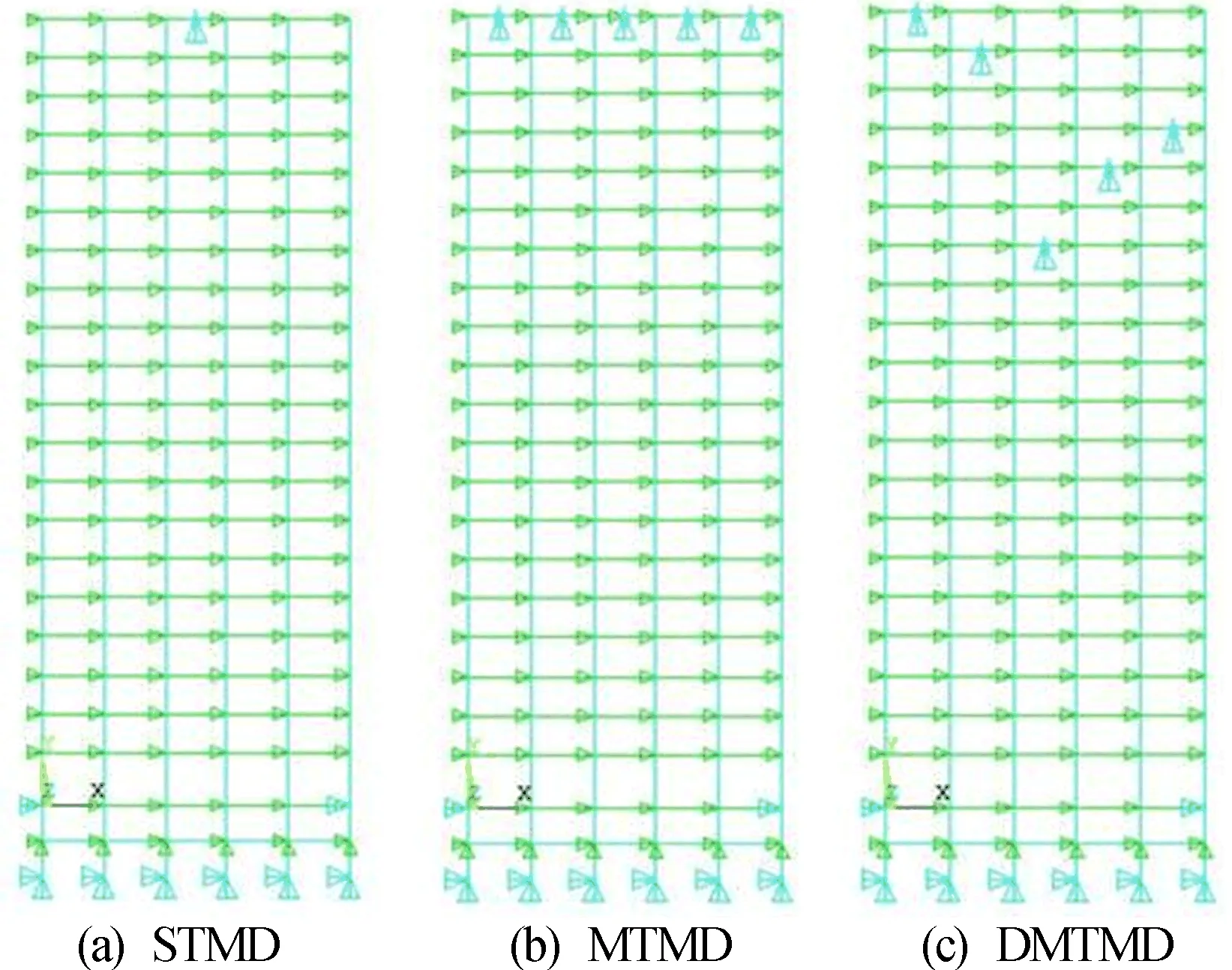
圖2 控制策略設計

2.2 評價指標

本文為了評價不同的控制策略,對不同阻尼器布置下的參數攝動結構進行時程分析。在進行時程分析過程中,引入控制性能評價指標J1、J2、J3,定義如下:

(1)

(2)

(3)

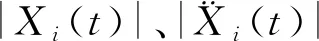
3 單因素控制魯棒性分析

建筑結構的模型參數如結構的剛度和質量參數難以用數學模型來精確描述,結構的不確定性會導致系統控制的不穩定和控制性能惡化。并且考慮到有限元模型和實際結構有一定的差距,因此考慮本結構質量和剛度參數攝動的控制魯棒性。比較當結構剛度變化+15%和-15%以及質量參數變化+15%和-15%的控制效果。本文選取Elcentro波、Taft波和天津波3條實際地震波,采用原始地震加速度記錄樣本采樣點間隔時間作為時程分析的時間步長。

3.1 剛度參數攝動控制魯棒性分析

將有限元模型剛度變化15%,即結構剛度變化+15%和-15%,保持阻尼器其余參數不變,考慮3種控制方案的控制效果魯棒性。3種控制方案的評價指標見表2、表3所列。

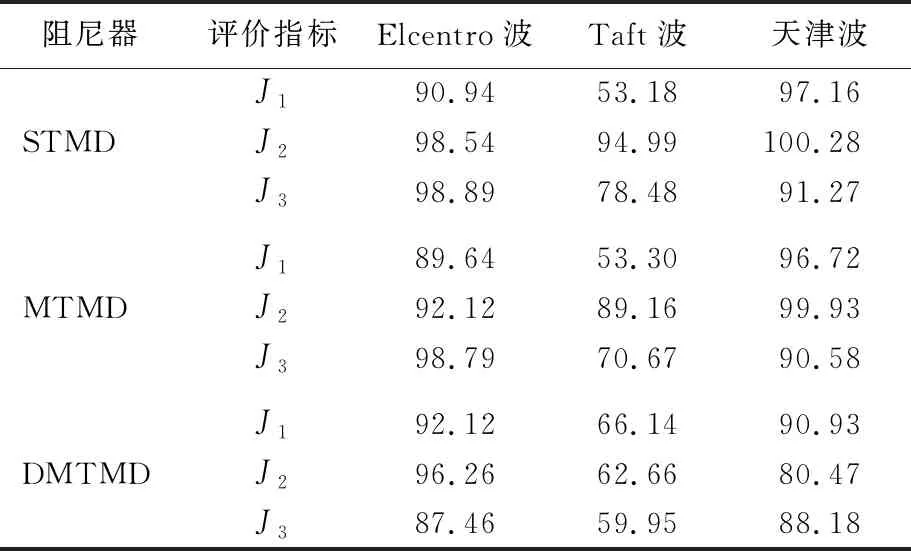
表2 ΔK=+15%K下3種控制方案比較 %

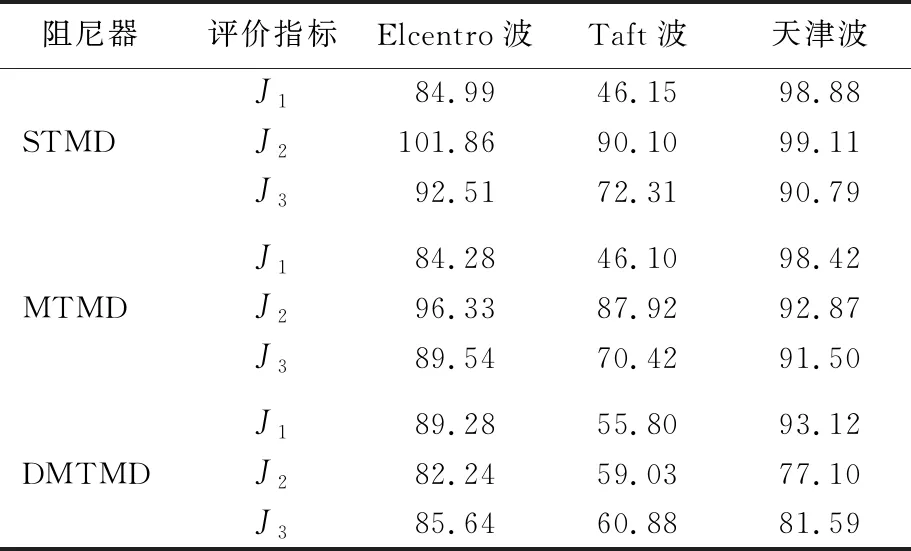
表3 ΔK=-15%K下3種控制方案比較 %

3.2 質量參數攝動控制魯棒性分析

將有限元模型質量變化15%,即結構質量變化+15%和-15%,保持阻尼器其余參數不變,考慮3種控制方案的控制效果魯棒性。3種控制方案的評價指標見表4、表5所列。

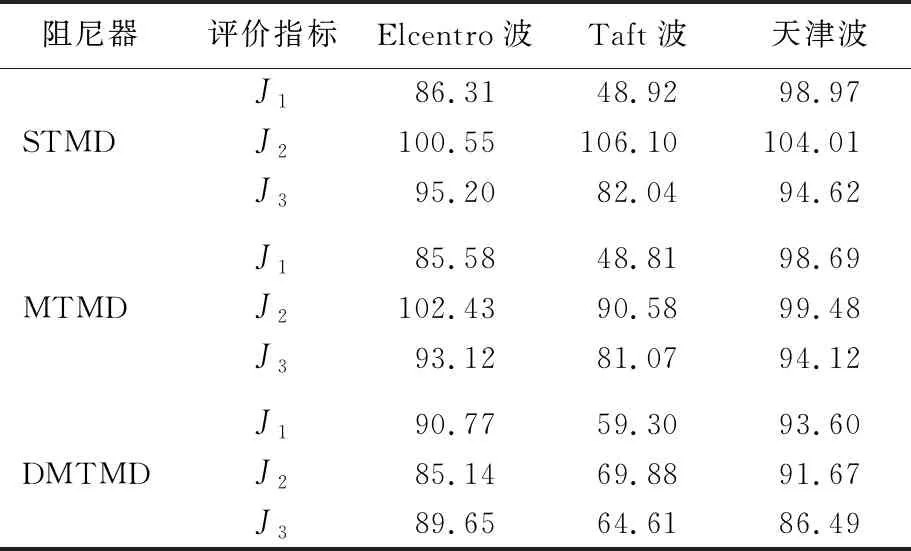
表4 ΔM=+15%M下3種控制方案比較 %

表5 ΔM=-15%M下3種控制方案比較 %

從表2～表5中可以看出,STMD控制方案的設計下,其存在參數失調而使結構振動有增大情況,在剛度或者質量變化15%時,STMD控制均存在不穩定特征,控制的頻率過窄,控制魯棒性較差。尤其是在質量參數攝動的情況下,控制效果更糟,J2(加速度)目標的控制效果均出現了增大的現象。MTMD控制相對穩定,但是仍有少部分評價指標在質量參數攝時下有大于1的情況。DMTMD的控制方案很穩定,因阻尼器的布置相對分散,故評價指標無大于1的情況,尤其在控制加速度和底層剪力方面比STMD、MTMD優越性較大。

4 多因素控制魯棒性分析

當將有限元模型剛度和質量同時變化15%,即結構剛度+15%、質量變化-15%,結構剛度-15%、質量變化+15%,結構剛度+15%、質量變化+15%,結構剛度-15%、質量變化-15%,保持阻尼器其余參數不變,考慮3種控制方案的控制效果魯棒性。

4.1 剛度和質量參數異向攝動控制魯棒性分析

剛度和質量參數異向攝動,即結構剛度+15%、質量變化-15%,結構剛度-15%、質量變化+15%。3種控制方案的評價指標見表6、表7所列。

表6 ΔK=+15%K、ΔM=-15%M下3種控制方案比較 %

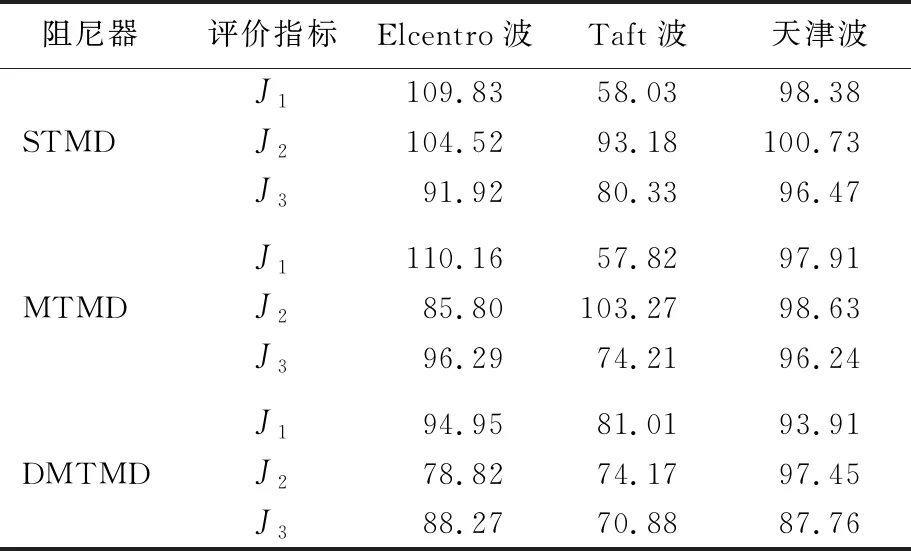
表7 ΔK=-15%K、ΔM=+15%M下3種控制方案比較 %

從表6、表7可以看出,在剛度和質量參數異向攝動時,STMD的控制魯棒性仍較差,尤其是在ΔK=-15%K、ΔM=+15%M的情況下。MTMD大于1的評價指標數目有所增加,控制魯棒性相對穩定,DMTMD的評價指標仍無大于1的情況,控制魯棒性較好。

4.2 剛度和質量參數同向攝動控制魯棒性分析

剛度和質量參數同向攝動,即結構剛度+15%、質量變化+15%,結構剛度-15%、質量變化-15%。3種控制方案的評價指標見表8、表9所列。

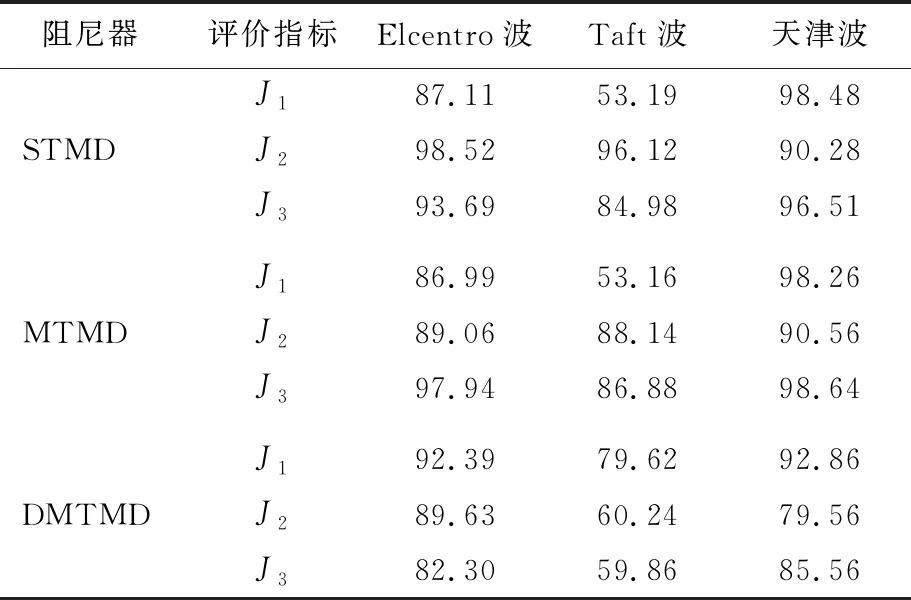
表8 ΔK=+15%K、ΔM=+15%M下3種控制方案比較 %

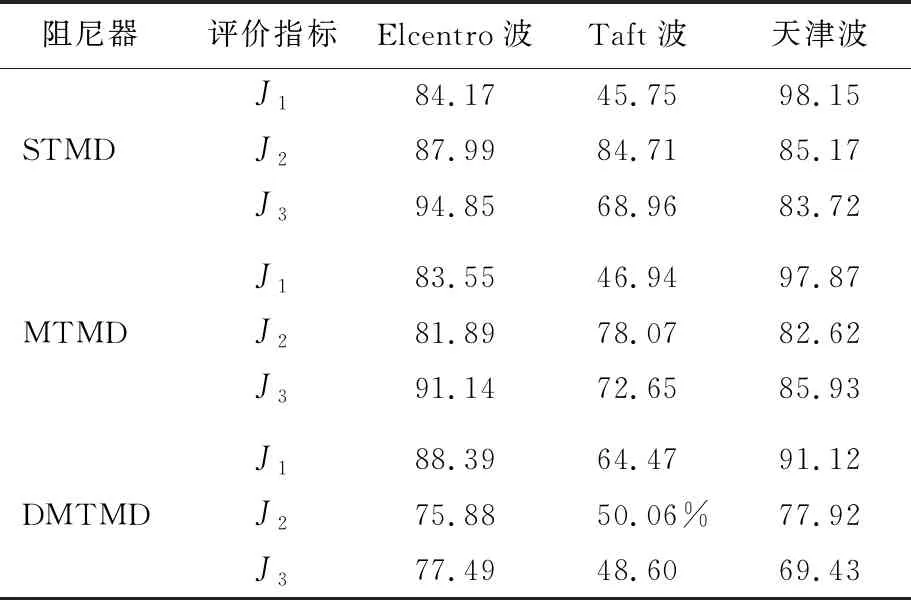
表9 ΔK=15%K、ΔM=-15%M下3種控制方案比較%

從表8、表9可以看出,STMD的評價指標雖然沒有大于1的情況,亦可以看出STMD的控制魯棒性最差,評價指標的數值大于MTMD和DMTMD。DMTMD的控制魯棒性較優越,可以用于高層建筑的地震反應控制中。

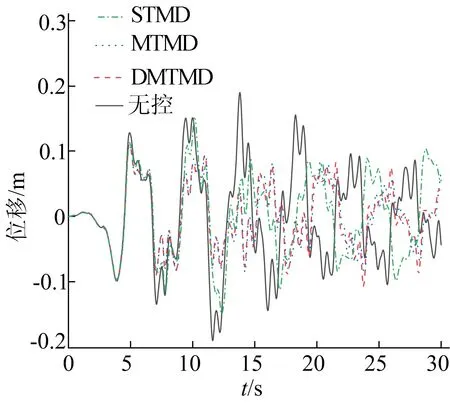
限于篇幅,本文僅給出Elcentro波、Taft波、天津波作用下,ΔK=-15%K、ΔM=+15%M攝動下3種控制策略的最大層間位移和頂層位移圖，如圖3～8所示。

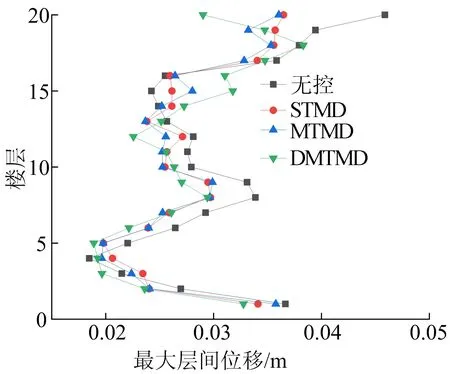
(a) Elcentro波作用下結構最大層間位移

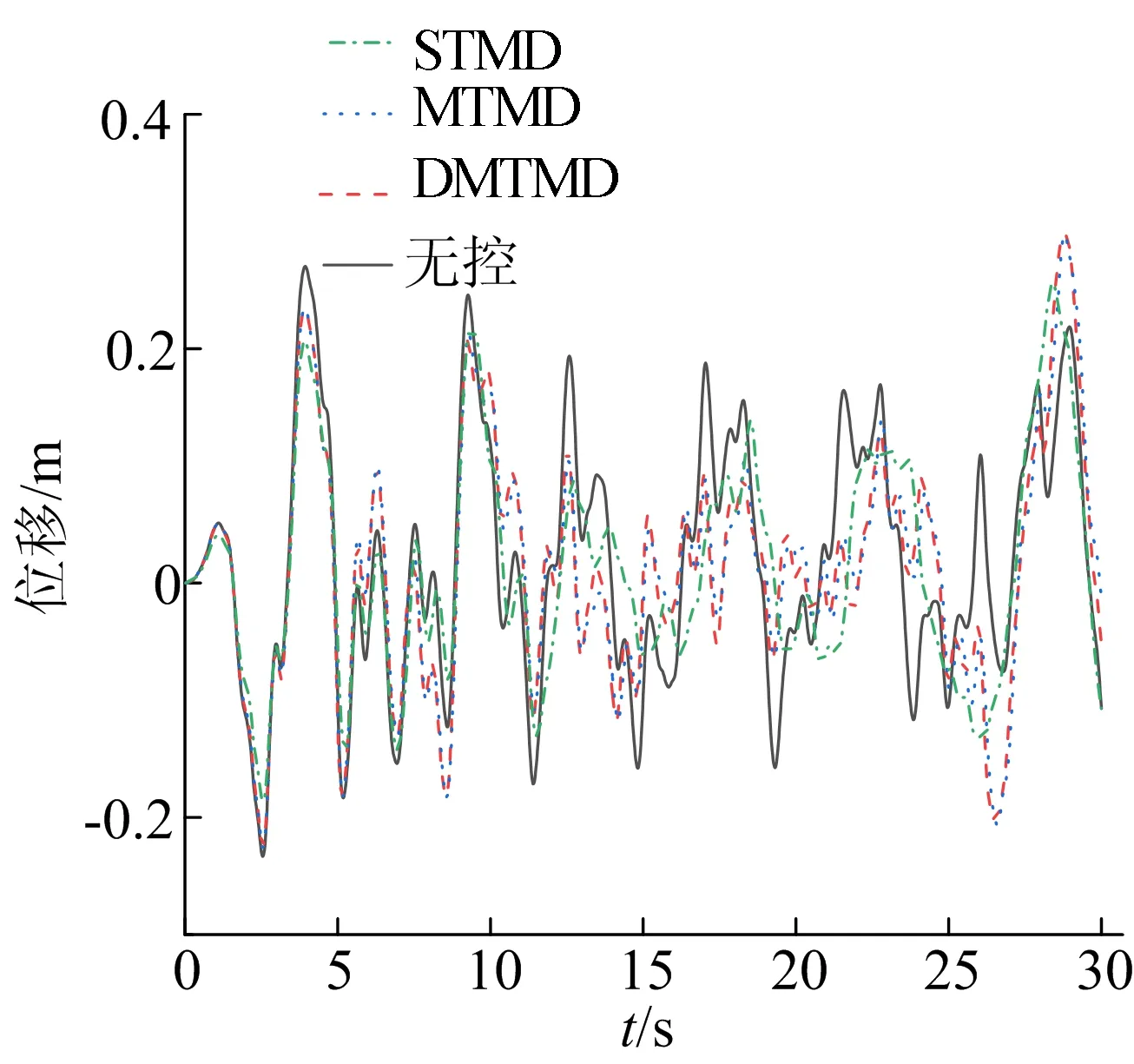
(b) Elcentro波作用下結構頂層位移時程曲線

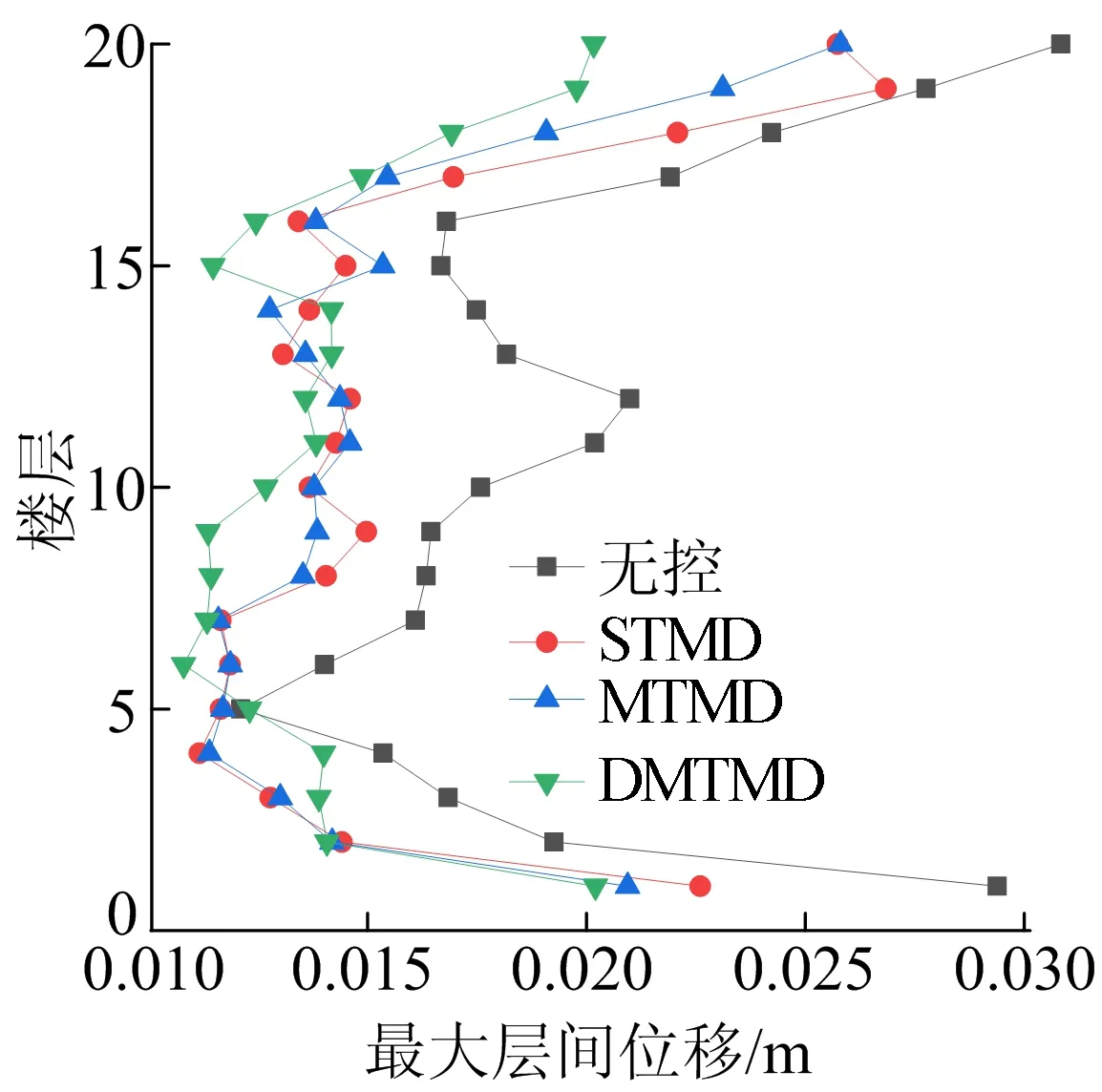
(c) Taft波作用下結構最大層間位移

(d) Taft波作用下結構頂層位移時程曲線

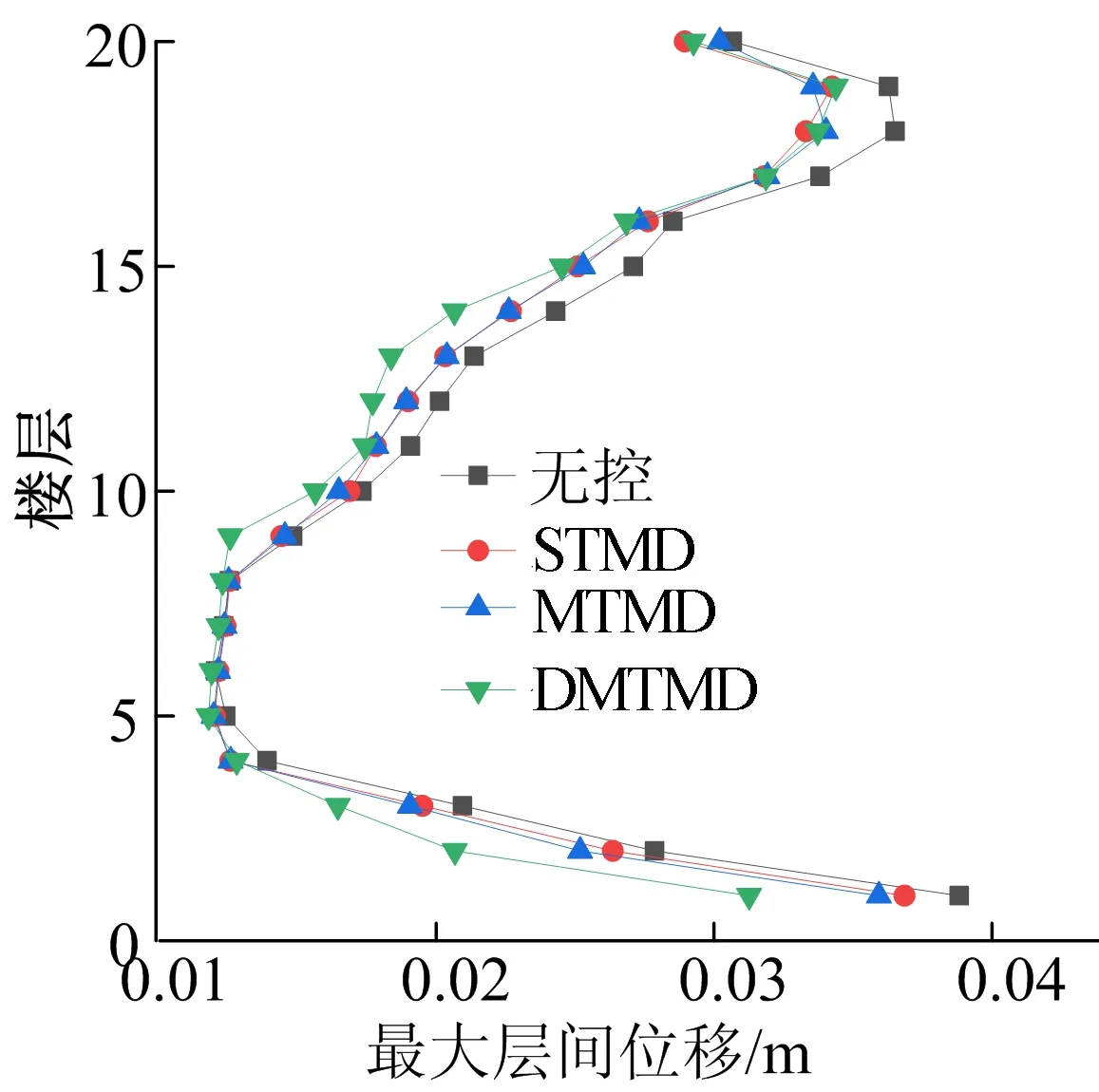
(e) 天津波作用下結構最大層間位移

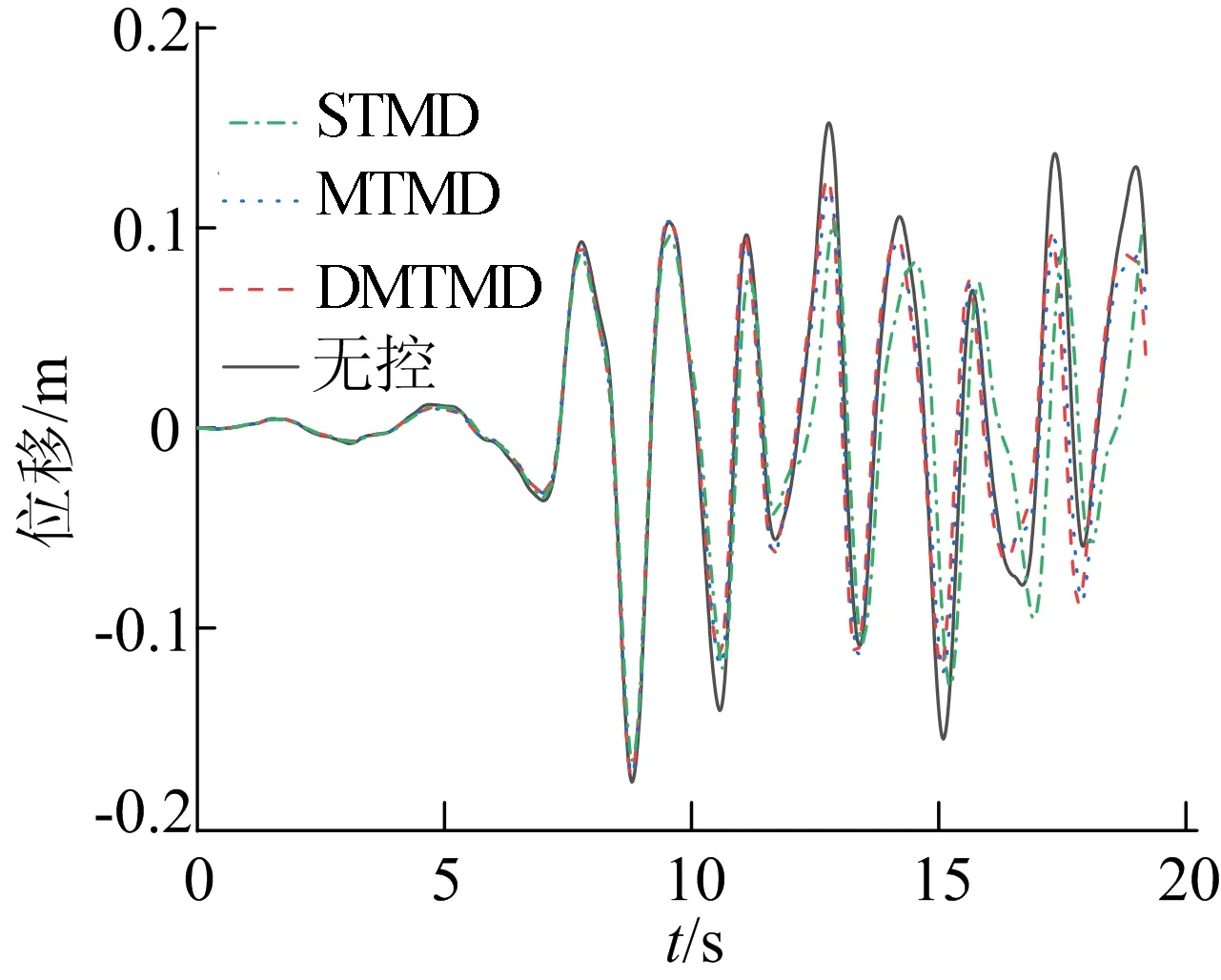
(f) 天津波作用下結構頂層位移時程曲線圖3 3種波作用下3種控制策略最大層間位移和頂層位移

5 結 論

本文從高層建筑結構振動控制的魯棒性出發,利用ANSYS軟件對MTMD建筑結構剛度和質量參數攝動的魯棒性進行研究。選取20層鋼框架Benchmark結構為模型,利用ANSYS有限元軟件對TMD阻尼器的3種不同布置方案進行魯棒性仿真分析。結果表明:剛度參數和質量參數攝動時,質量參數攝動對控制效果的影響比剛度參數的影響大;質量參數增加對控制效果的影響比質量參數減小的影響大。本文采用的將MTMD沿結構振型最大處的位置依次布置DMTMD的控制策略,具有良好的魯棒性,優于相同質量比情況下的僅在結構頂層布置STMD和僅在結構頂層布置MTMD的控制策略。