信號交叉口左轉非機動車交通沖突分析

周智文, 馬健霄, 王冠森

(南京林業大學 汽車與交通工程學院,江蘇 南京 210037)

長期以來,我國城市道路常有機動車與非機動車(簡稱“機非”)交通混合行駛的情況。城市道路一般使用隔離欄或標線以分離機非交通,因此交通沖突較少。而在交叉口,機非車流混行易導致交叉口頻發交通事故,降低通行效率。在交叉口非機動車流中,對交叉口安全通行影響最明顯的就是左轉機非車輛間的相互干擾[1-2]。針對這種矛盾,目前主要有5種非機動車左轉過街的組織方法:左轉機非同時左轉、左轉非機動車二次過街、設置左轉非機動車待轉區、左轉非機動車綠燈先亮及設置左轉非機動車單獨左轉相位[3]。但各方法適用條件模糊,難以比較其優劣。

在交叉口非機動車交通特性方面,目前研究大多通過視頻分析法得出各交通流相關參數,并研究各參數之間的相關性及其影響因素,提出假定模型,通過實際數據擬合求解參數,進行驗證[4-6]。而求解模型關鍵在于確定模型影響因素和模型的形式,相關研究主要基于機非車輛的沖突機理分析各因素與機非沖突的關系[7-8],而已有研究一方面忽略了混合非機動車與機動車的沖突研究,另一方面缺乏定量分析具體流向的非機動車交叉沖突和膨脹沖突[9]。

目前,針對機非沖突下的通行效率主要有2種研究方法:① 基于實測的飽和流率折減系數法[10],該方法計算簡單,但為了保證真實可靠,需大量實測數據;② 基于可接受穿越間隙理論,該方法適應性強,但計算復雜。對于多種非機動車左轉組織方法的系統評價以及左轉非機動車交通安全的相關研究較少。對于交叉口機非沖突的研究,大多僅考慮自行車流,缺乏對電動自行車的研究;沖突研究的重點偏向于機非沖突對交叉口通行效率或安全性的影響[11-12],缺乏綜合考慮。針對交通沖突最為劇烈的左轉非機動車,雖有多種改進組織方法,但大都缺乏合理的評價指標。

本文以左轉非機動車與機動車的交叉沖突和膨脹沖突為研究對象,分析機非沖突對機動車通行能力的影響,并構建機非沖突數模型。

1 左轉非機動車與機動車沖突分析

1.1 交叉口左轉非機動車與機動車交叉沖突

目前,主要有2種方式分析信號控制交叉口的左轉非機動車流線:方式1,采用和機動車相同的方式通過交叉口,如圖1所示;方式2,采用和行人相同的方式通過交叉口,如圖2所示。

對于左轉非機動車與機動車交叉沖突點,選擇最常見的四相位信號控制交叉口進行分析。四相位信號控制是指各進口道直行和左轉信號相位分離、右轉信號常綠的信號控制方式。四相位信號控制交叉口中,某一進口道非機動車分別采用2種左轉方式后與機動車發生沖突的沖突點示意圖如圖3所示。從圖3可以看出,在四相位信號控制交叉口中,左轉方式1共有2處機非交叉沖突點;左轉方式2通過無導流島交叉口時共有4處機非沖突點;左轉方式2通過有導流島交叉口時共有2處機非沖突點。

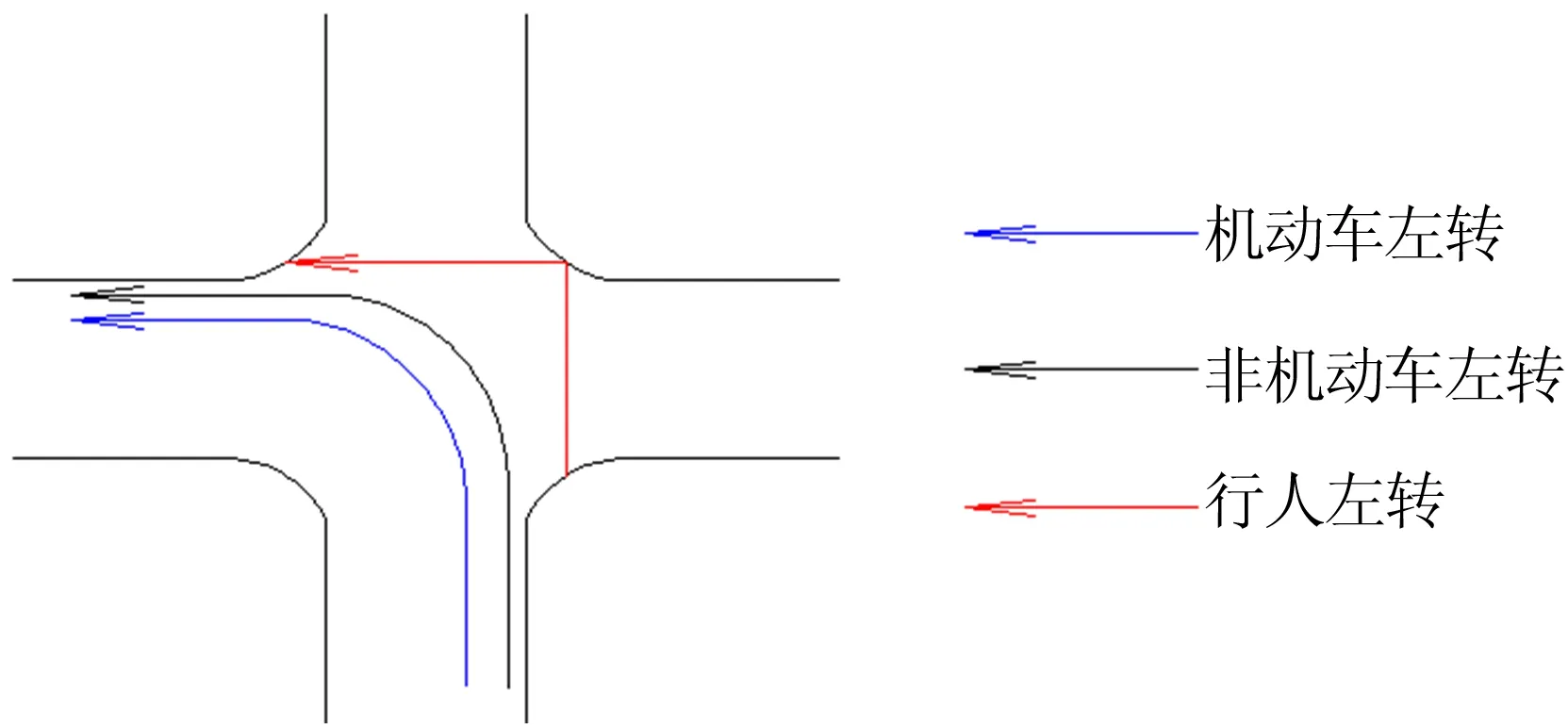
圖1 非機動車與機動車采用相同方式通過(方式1)

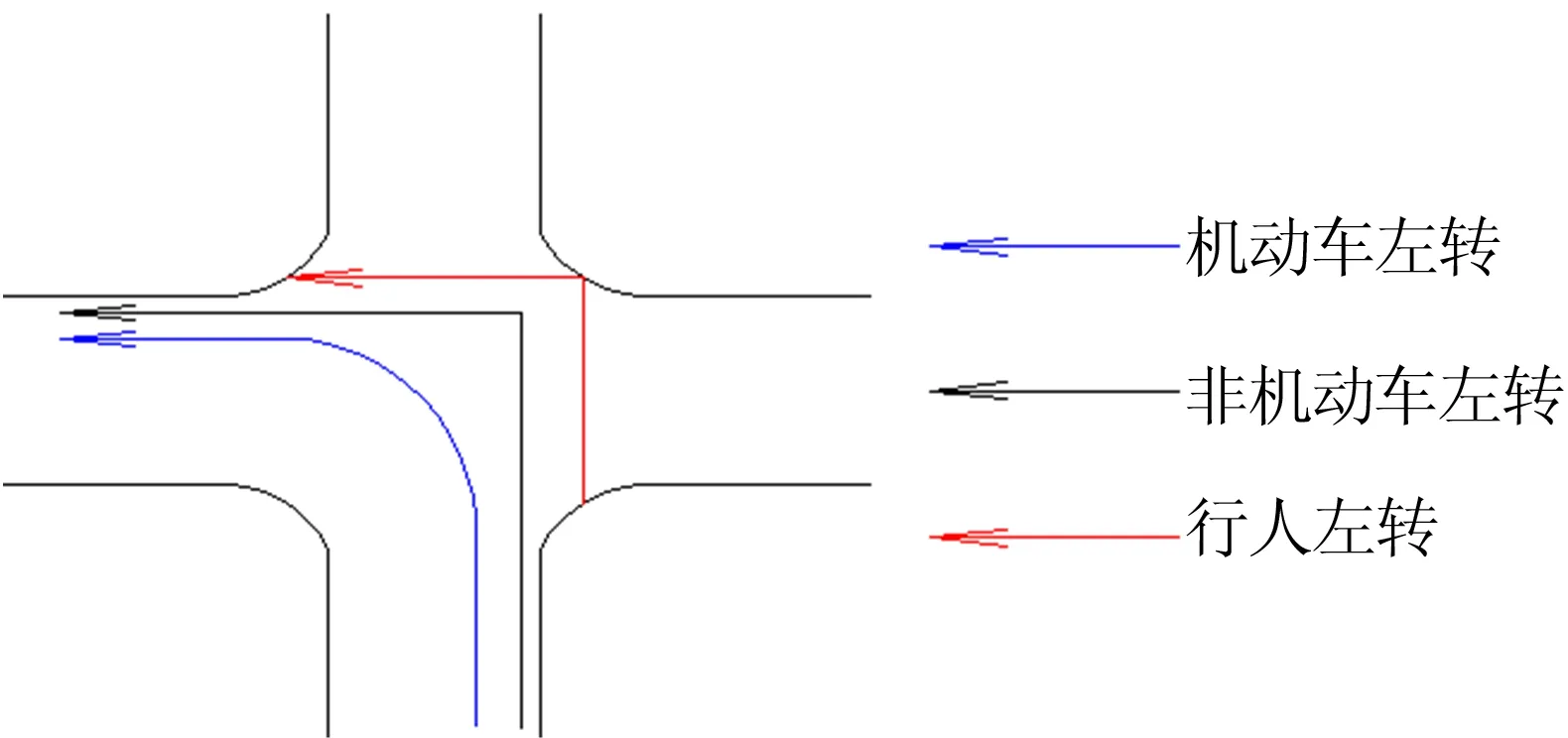
圖2 非機動車與行人采用相同方式通過(方式2)

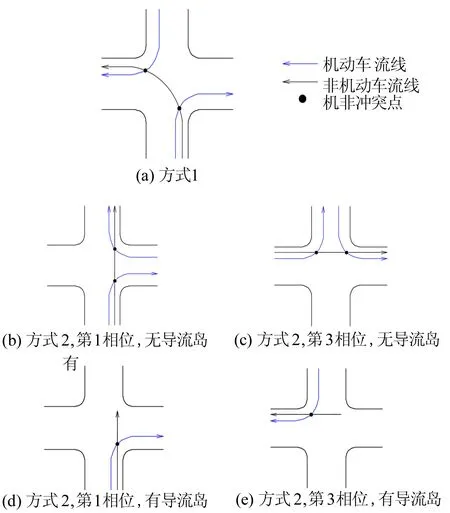
圖3 四相位信號控制交叉口機非沖突點

1.2 交叉口左轉非機動車與機動車膨脹沖突

非機動車的膨脹效應是指在信號交叉口某一進口道非機動車無通行權期間內,非機動車在停止線后排隊等候。此時非機動車較為密集,橫向占用寬度較小。當轉至綠燈信號后,非機動車加速駛入交叉口,其橫向寬度要求增大,非機動車流向兩側擴張,車流整體呈擴散狀態。

非機動車流的膨脹效應將與同向行駛的機動車產生沖突。因此,分析非機動車膨脹現象、建立非機動車膨脹模型是研究非機動車膨脹現象與同向機動車產生沖突的基礎。交叉口左轉非機動車膨脹效應如圖4所示。

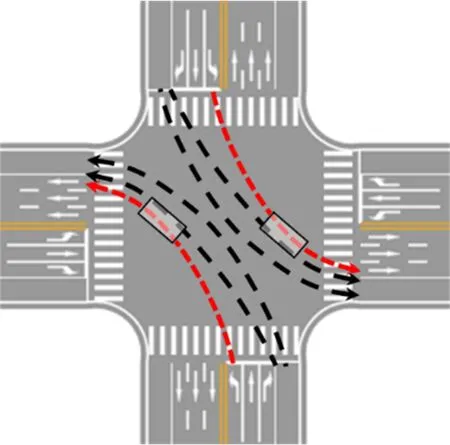
圖4 交叉口左轉非機動車膨脹效應

2 機非沖突對機動車通行能力的影響

2.1 機非交叉沖突對交叉口通行能力的影響

在四相位信號控制交叉口,機非交叉沖突過程較為復雜,其影響可歸結為以下2類:

(1) 綠燈初期非機動車占用沖突區影響。在綠燈初期,非機動車由于加速性能較好,先于機動車進入機非沖突區。該時段內,機動車無法駛入沖突區,需等待已駛入沖突區內的非機動車駛離后方可進入,實際通行能力降低。

(2) 非機動車穿越沖突區造成的影響。當機動車流占據沖突區時,非機動車將利用可接受穿越時間間隙穿越沖突區,因此,即將駛入沖突區的機動車會采取制動措施避免與前車相撞,進而降低整體機動車流速度。而當非機動車全部穿越沖突區后,機動車流將加速通過沖突區。此時段內,機動車的速度波動進一步降低其通行能力。

2.1.1 非機動車到達分布分析

城市道路交叉口非機動車的到達可用離散型分布進行描述。離散型分布主要有泊松分布、二項分布及負二項分布3種。其中,泊松分布常用于描述交通量不大且沒有交通信號干擾的車輛到達分布,而在國內的城市道路上,非機動車交通量大,且存在著交通信號及其他因素干擾,不適宜用泊松分布描述。因此,本文采用二項分布和負二項分布描述不同狀態下的自行車到達。

當非機動車流交通量大,自由行駛機會少時,可用二項分布描述該交通流,即

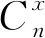
(1)

p=(m-S2)/m

(2)

n=m2/(m-S2)

(3)

其中:P(x)為非機動車道進口道周期內到達x輛非機動車的概率;x為非機動車道進口道周期內到達的非機動車數量;m為樣本均值;S2為樣本方差。

而當非機動車流波動性較大亦或計數周期包含高峰時段和非高峰時段時,負二項分布擬合觀測數據較為準確:

(4)

p=m/S2

(5)

k=m2/(S2-m)

(6)

2.1.2 綠燈初期非機動車占用沖突區影響分析

對綠燈初期非機動車占用沖突區的時間進行分析。令非機動車在綠燈初期通過沖突區所需時間為T1。密集通過沖突區的車輛是在紅燈時間Tr和T1內累積的,可以得出:

(Tr+T1)λn=NtBT1

(7)

(8)

其中:λn為非機動車到達率,非機動車整體到達分布呈二項分布或負二項分布;Nt為沖突區非機動車斷面飽和流率,建議值為0.061 3輛/(s·m)[13];B為沖突區非機動車流寬度。

在T1時段內,機動車無法通過沖突區,需等待沖突區內全部非機動車離開后方可通行[14]。假設非機動車到達分布呈負二項分布,則在某時段T2內,沖突區無非機動車到達的概率為:

(9)

令Tg為有效綠燈時間,則沖突區無非機動車的時間為P0(Tg-T1)。設機動車流以流率q0通過沖突區,則可得出周期內機動車在沖突區無非機動車時段通過的交通量為:

Qn=q0P0(Tg-T1)/3 600

(10)

2.1.3 非機動車穿越沖突區造成的影響分析

對非機動車穿越機動車流造成的影響進行分析,根據交通流理論可得出機動車車流的流率均值[15]為:

(11)

其中:v1、v2為機動車流減速前、后的平均速度;q(v)為機動車交通量關于速度v的函數。

令非機動車通過沖突區的時間為T3,則非機動車一次穿越過程中能通過的車輛數為:

z=2q12T3

(12)

沖突區有非機動車穿越的概率P1應為非機動車到達沖突區,且機動車車輛中存在非機動車可接受穿越時間間隙的概率。假設機動車與非機動車到達相互獨立,則

z=P(x>0)P(t≥tnt)=

(1-P(x=0))P(t≥tnt)

(13)

其中:t為機動車流車頭時距;tnt為非機動車可接受穿越時間間隙。

假設機動車流車頭時距t服從移位負指數分布,則可得在時段T2內P1為:

(14)

(15)

因此,機動車流在非機動車穿越影響時段內通過的車輛數Qi為:

(16)

2.1.4 機非交叉沖突區機動車通行能力研究

根據上述分析可以得出,在機非交叉沖突區的非機動車影響下,機動車通行能力為:

Qc=(Qn+Qi)(3 600/C)

(17)

其中,C為交叉口信號周期時長。

則可求得非機動車與機動車交叉沖突對機動車通行能力影響系數為:

(18)

2.2 機非膨脹沖突對交叉口通行能力的影響

在信號控制交叉口,若非機動車直接左轉通過交叉口,則控制信號轉至左轉相位時,左轉機非車輛同時放行。當左轉非機動車交通量較小時,非機動車膨脹對機動車產生的影響極小;但隨著左轉非機動車交通量的增加,車流膨脹寬度也將增大,直接降低同向進口道左轉機動車通行能力。

利用南京市“珠江路-太平北路”與“中山北路-模范中路”2個交叉口的航拍視頻進行機非膨脹沖突的影響研究,分析直接左轉非機動車最大橫向行駛寬度Bmax和左轉機動車通過交叉口時間之間的關系。研究得出,當Bmax為2.5 m及以下時,左轉機動車幾乎不受影響。但是隨著Bmax增大,機動車左轉通過交叉口的平均時間逐漸增大,此時Bmax和機動車左轉通過交叉口的時間呈正相關關系。

同向進口道左轉機動車間受左轉非機動膨脹沖突影響,通過交叉口時延誤增加,通行能力降低。經過相關交叉口實測調查,左轉機動車無左轉非機動車影響直接通過交叉口的平均時間為10.48 s,則可得出左轉非機動車不同Bmax的情況下,機動車通過交叉口時間延誤t延與左轉機動車的通行能力調整系數f膨,見表1所列。

表1 不同Bmax下的t延與f膨

左轉機動車f膨可應用于交叉口左轉機動車飽和流率及通行能力的調整。左轉非機動車Bmax增加將不斷降低左轉機動車通行能力,但由于交叉口空間資源有限,交叉口左轉非機動車Bmax有極限值。通過多次觀測調查,左轉非機動車Bmax約為7.0 m。在左轉非機動車橫向行駛寬度達到6.5 m以上時,左轉非機動車流會占據交叉口核心區域,并截斷左轉機動車流。

3 交叉口機非沖突數模型構建

本文通過對南京市“珠江路-太平北路”與“中山北路-模范中路”2個交叉口的實地調查,獲取機動車交通量、非機動車交通量、機非交叉沖突數等相關數據,構建機非交叉沖突數模型。

文獻[16]構建了交叉口3種類型機非交通沖突的沖突數預測模型,機非交通沖突的3種類型分別為:

類型1同向進口道右轉機動車與直行非機動車交通沖突。

類型2相鄰進口道右轉機動車與直行非機動車交通沖突。

類型3對向進口道左轉機動車與直行非機動車交通沖突。

3種類型機非交通沖突的沖突數預測模型[16]為:

(19)

(20)

(21)

其中:ui為3種類型機非交通沖突數的預測值(i=1,2,3);X機動車i為3種類型機非交通沖突的機動車交通量(i=1,2,3);X非機動車i為3種類型機非交通沖突的非機動車交通量(i=1,2,3)。

文獻[16]通過構建機動車與非機動車交通量的廣義線性機非交通沖突模型,預測3種機非交通沖突數,但該模型中非機動車的影響因素只考慮總體交通量,未考慮自行車和電動自行車的差異性。

3.1 交叉口機非交叉沖突數模型構建

針對四相位信號控制交叉口構建左轉非機動車與機動車交叉沖突數模型,分析左轉非機動車與機動車交叉沖突點,主要有2處:① 左轉非機動車與同向進口道右轉機動車交叉沖突(沖突點1);② 左轉非機動車與對向進口道右轉機動車交叉沖突(沖突點2)。

構建沖突點1的交叉沖突數模型為:

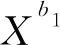
(22)

其中:C1為沖突點1的交叉沖突數;X同右機為同向進口道右轉機動車交通量;X自為左轉自行車交通量;X電為左轉電動自行車交通量;a1、b1、d1、e1為相關系數。

以15 min為時間間隔獲取沖突點1的C1、X同右機、X自、X電數據,見表2所列。

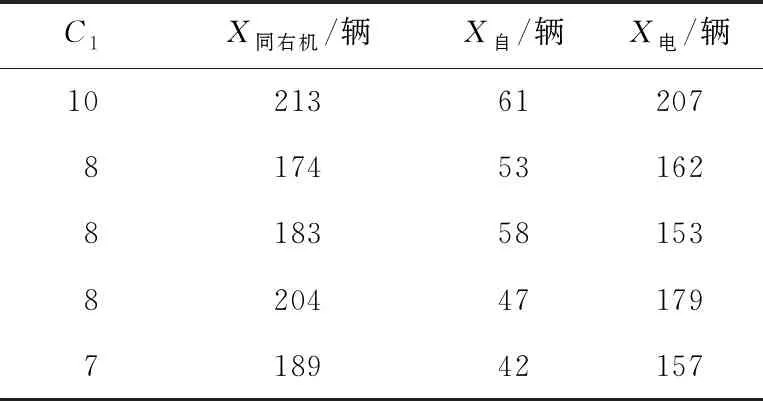
表2 沖突點1的交叉沖突數模型數據

將表2數據代入(22)式,得到模型為:

(23)

為檢驗該模型的預測能力,利用2組相關數據進行模型校核,相關數據和由(23)式預測的沖突數見表3所列。

表3 沖突點1的交叉沖突數模型校核結果

從表3可以看出,該交叉口沖突點1的交叉沖突數模型(23)式預測能力較好,能夠反映此沖突的實際狀況,可應用于沖突預測和交叉口安全評價。

建立沖突點2的交叉沖突數模型為:

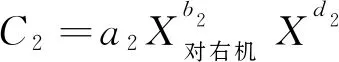
(24)

其中:C2為沖突點2的交叉沖突數;X對右機為對向進口道右轉機動車交通量;a2、b2、d2、e2為相關系數。

以15 min為時間間隔獲取沖突點2的C2、X對右機、X自、X電數據,見表4所列。

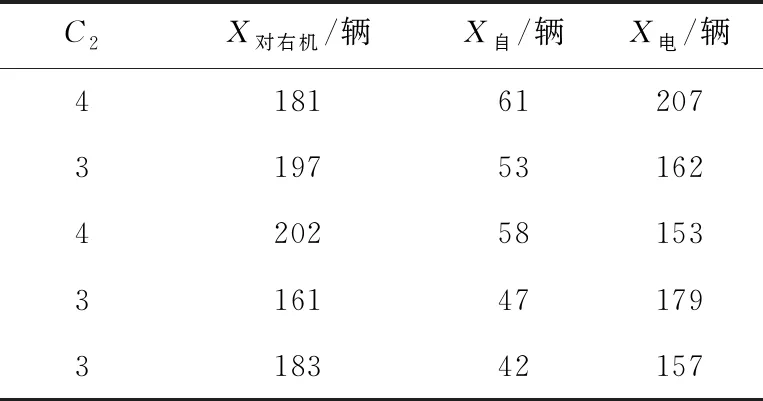
表4 沖突點2的交叉沖突數模型數據

將表4數據代入(24)式,得到模型為:

(25)

為檢驗該模型的預測能力,利用2組相關數據進行模型校核,相關數據和由(25)式預測的沖突數見表5所列。

表5 沖突點2的交叉沖突數模型校核結果

從表5可以看出,該交叉口沖突點2的交叉沖突數模型(25)式預測能力較好,能夠反映此沖突的實際狀況,可應用于沖突預測和交叉口安全評價。

3.2 交叉口機非膨脹沖突數模型構建

通過分析機非膨脹沖突的產生機理,得到影響交叉口左轉機動車與非機動車膨脹沖突的3個最直接因素,分別為機動車交通量、非機動車交通量及交叉口渠化狀況。

建立交叉口左轉非機動車與同向進口道左轉機動車膨脹(簡稱“左轉膨脹點”)沖突數模型為:

(26)

其中:C3為左轉膨脹點的沖突數;X同左機為同向進口道左轉機動車道交通量;D1為交叉口進口道最外側左轉機動車道外側邊線至非機動車道內側邊線的距離;a3、b3、d3、e3為相關系數。

以1 h為時間間隔獲取左轉膨脹點的C3、X同左機、X自、X電、D1數據,見表6所列。

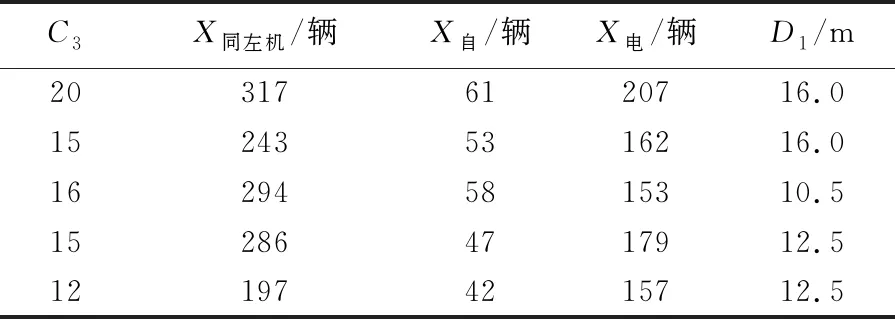
表6 左轉膨脹點沖突數模型數據

將表6數據代入(26)式,得到模型為:

(27)

為檢驗該模型的預測能力,利用2組相關數據進行模型校核,相關數據和由(27)式預測的沖突數見表7所列。

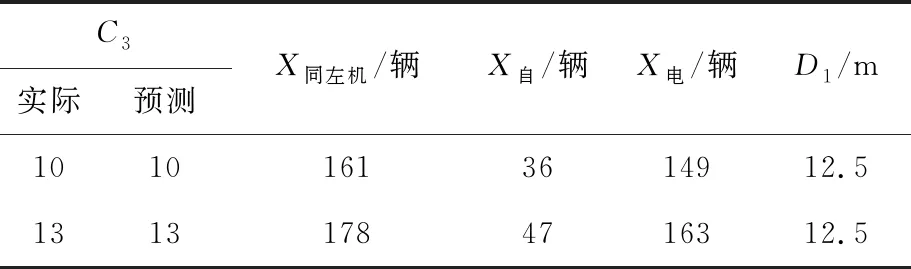
表7 左轉膨脹點沖突數模型校核結果

從表7可以看出,該交叉口左轉膨脹點沖突數模型(27)式預測能力較好,能夠反映此沖突的實際狀況,可應用于沖突預測和交叉口安全評價。

4 結 論

本文從交通沖突的角度出發,研究交叉口左轉非機動車與機動車沖突原理,將非機動車對機動車通行能力的影響細分為綠燈初期非機動車占用沖突區影響與非機動車穿越沖突區造成的影響;進一步構建機非交叉沖突和膨脹沖突的沖突數模型,通過實測數據進行擬合,得出不同沖突下交叉口左轉機動車通行能力影響系數。

相關沖突和各優化方法對非機動車通行效率的影響對于交叉口的整體優化同樣具有重要的意義,下一步研究將綜合考慮這些影響因素,使得優化方法能令交叉口整體優化度最好。