基于事件驅動的隨機多智能體系統的一致性
馬文周, 柏曉明
(合肥工業大學 數學學院,安徽 合肥 230601)
0 引 言
多智能體系統通常是指由大量具有通信連接的智能體所組成的系統。借助智能體間的信息交換,系統在整體上可以呈現出單一智能體所不具備的行為,這種系統在生物、工程和社會等領域廣泛存在。多智能體系統的一個基本問題就是趨同問題;趨同問題就是設計合適的分布式協議,最終使多智能體系統的每個智能體的狀態達到一致。文獻[1-8]中的控制協議大都建立在多智能體之間的連續通訊的基礎上,這將消耗大量的通訊資源。為了達到節省通訊資源的目的,事件驅動方法被引入了網絡控制系統中,即只有在滿足事件驅動觸發條件時,多智能體之間才互相通訊。
基于事件驅動的控制是現在網絡控制系統中的一個熱門話題[9-18]。文獻[9]證明了經典事件驅動策略控制下,控制系統無芝諾行為發生,可有效節省通訊資源。文獻[10-16]分別探討了在無噪聲假設下不同類型有效的事件驅動觸發方案以及事件驅動控制協議,其中文獻[11]提出了一種區別于以往的集中事件觸發方案,能更有效地降低智能體間通訊頻率,且避免了芝諾行為的發生。文獻[17-18]探討了在有乘性系統噪聲存在下的帶事件驅動的多智能體系統一致性問題,并且分別給出了在有噪聲假設下的有效的事件觸發方案以及事件驅動控制協議,其中文獻[17]通過隨機變量期望的上下界函數以及引入的一個內部動態變量在保證系統的均方一致性的同時避免了芝諾行為的發生;文獻[18]通過隨機變量的期望以及引入一個內部變量的方法保證系統的均方一致性與無芝諾行為發生。
本文參考文獻[17-18]方法,采用文獻[11]的事件驅動控制協議證明了在該事件驅動控制下帶領導者的線性隨機多智能體系統可以達到均方一致,且無芝諾行為發生;最后通過數值模擬,驗證了理論分析的正確性。
本文中‖·‖表示向量2范數與矩陣的2誘導范數。(Ω,F,{Ft}t≥0,P)為完備概率空間,其中,Ω為樣本空間;F為σ-域;{Ft}t≥0為濾子;P為概率測度。
1 問題描述
1.1 預備知識
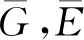
A=[aij]∈RN×N為圖G的鄰接矩陣,當且僅當(i,j)∈E時,aij=1,aii=0,其余aij=0。定義對角矩陣D=diag{d1,d2,…,dN},當且僅當頂點i可以從領導者處獲取信息時,di=1,其余di=0。定義拉普拉斯矩陣為:
記H=L+D。
考慮帶N個跟隨者的多智能體趨同控制系統:
(1)
其中:i=1,2,…,N;xi(t)∈Rn表示多智能體狀態;x0(t)表示領導者狀態;ui(t)∈Rn表示智能體i的控制輸入;A∈Rn×n、B∈Rn×m、C∈Rn×n都為多常數矩陣;wi(t)表示定義在概率空間(Ω,F,{Ft}t≥0,P)上的一維布朗運動。
1.2 集中事件驅動控制
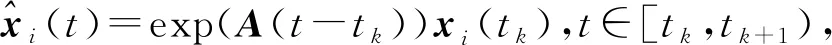
定義測量誤差為:
(2)
本文使用事件驅動控制協議為:
(3)
其中,K=BTP,P為滿足假設條件的正定矩陣。跟隨者i的控制輸入由上一次事件驅動時跟隨者與領導者的狀態以及時間間隔t-tk計算得來。
用δi(t)=xi(t)-x0(t)表示跟隨者i逼近領導者狀態的程度。
dδ(t)=(IN×N?A)δ(t)-(H?BK)(δ(t)+
e(t))dt+(IN×N?C)δ(t)dw(t)
(4)
事件觸發時間序列{tk}定義如下:
tk+1=inf{t>tk|E‖(IN?N?K)e(t)‖2-
βE(‖H?K)δ(t)‖2)-λ(t)>0}
(5)
其中
E‖(IN×N?K)e(t)‖2)-σλ(t)
(6)
且β,σ>0;λN>0為矩陣H的最大特征值。領導者的所有跟隨者共享同一個事件觸發時間序列。
假設1 代數黎卡提不等式
CTPC+I<0
(7)
有正定解。其中,λ1、λN分別為矩陣H的最小、最大特征值。
本文使用文獻[11]中事件驅動控制策略,參考文獻[17-18],在其事件觸發機制中引入隨機變量的期望以及一個內部動態變量,使該事件驅動控制策略在有乘性噪聲的環境中依舊能有效地避免芝諾行為,且文章事件觸發機制中考慮了增益矩陣K,這與文獻[17-18]均不相同。
2 引理及定理
引理1[19]當且僅當圖G是連通圖時,由圖G決定的矩陣H正定。
顯然,若圖G中存在m個連通分量,且每一個連通分量都可以從領導者處獲取信息,各連通分量間互相不通訊。單獨每個連通分量與領導者決定的矩陣Hi正定,由圖G決定的矩陣:
也為正定矩陣。
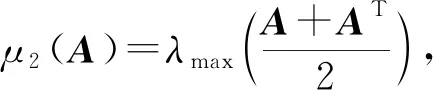
(8)
若μ2(A)<0,則
μ2(A)≥-(‖A-1‖)-1≥-‖A‖
(9)

引理4[22](Gronwall不等式) 設r(t)、h(t)、y(t)是定義在[a,b]上的連續函數,r(t)≥0,h(t)≥0,且對?t∈[a,b],都有:
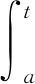
則
若h(t)為常數h,則
引理5系統(1)中,對于?t∈[tk,tk+1),E(‖(IN?N?K)e(t)‖2)與E(‖(H?K)δ(t)‖2)分別存在如下上界函數、下界函數:
Γ1(δ(tk),t-tk)≥E(‖(IN×N?K)e(t)‖2)
(10)
Γ2(δ(tk),t-tk)≤E(‖(H?K)δ(t)‖2)
(11)
其中
Γ1(δ(tk),t-tk)=
(exp{2μ2(A)(t-tk)}-exp{a(t-tk)});
Γ2(δ(tk),t-tk)=
(exp{-b(t-tk)}-exp{2μ2(A)(t-tk)})+
E‖H?Kδ(tk)‖2exp{-b(t-tk)};
λmin(KTK)為矩陣KTK的最小非0特征值。
證明設
Γ(t)=‖(IN×N?K)e(t)‖2,t∈[tk,tk+1)。
由Dynkin公式得:
E(‖(IN×N?K)e(t+ε)‖2|Ft)=
‖(IN×N?K)e(t)‖2+
eT(s)(IN×N?CTKTKC)e(s))ds|Ft]
由ε的任意性以及富比尼定理可知:
D+EΓ(t)=2EeT(t)(IN×N?KTKA)e(t)+
EeT(t)(IN×N?CTKTKC)e(t)≤
‖KKT‖)E‖(IN×N?K)e(t)‖2+
由(8)式得:
E‖(H?K)δ(tk)‖2exp{2μ2(A)(t-tk)},
其中,λmin(HH?KTK)為矩陣HH?KTK的最小非0特征值。
由(8)式、(9)式易知a-2μ2(A)>0。由引理3及
Γ(tk)=E(‖(IN?N?K)e(tk)‖2)=0,
即得(10)式。
同理,可設
Φ(t)=-E‖(H?K)δ(t)‖2,
得
D+(EΦ(t))≤
E‖(H?K)δ(tk)‖2exp{2μ2(A)(t-tk)}。
由比較法則以及Φ(tk)=-E‖(H?K)δ(tk)‖2即得(11)式。
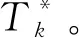
證明設
顯然有S1>0,S2>0。
等式Γ1(δ(tk),T)=βΓ2(δ(tk),T)兩邊同時除以exp{2μ2(A)T},則有:
S1(exp{(a-2μ2(A))T}-1)=
βS2(exp{(-b-2μ2(A))T}-1)+
βexp{(-b-2μ2(A))T}。
設
f(T)=S1(exp{(a-2μ2(A))T}-1)-
βS2(exp{(-b-2μ2(A))T}-1)-
βexp{(-b-2μ2(A))T}
(12)
而
f(0)=-1<0
(13)

(14)
f′(T)=(a-2μ2(A))S1exp{(a-2μ2(A))T}+
(b+2μ2(A))βS2exp{(-b-2μ2(A))T}+
(b+2μ2(A))βexp{(-b-2μ2(A))T}>0
(15)
故f(T)在T∈(0,+∞)上單調遞增。由(13)式、(14)式可知,方程f(T)=0存在唯一大于0的解T*。
當a≥b,μ2(A)>0時,設
g(T)=S1(exp((a+2μ2(A))T)-1)-
βS2(exp((-a-2μ2(A))T)-1)-
βexp((-a-2μ2(A))T),
顯然g(T)也是單調遞增函數,且f(T)≤g(T)。
同上易證,存在T*,使得0=g(T*)≥f(T*)。
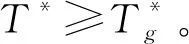
記y=exp{(a+2μ2(A))T},令g(T)=0,即
S1y2+(βS2-S1)y-βS2-β=0。
解上述方程,舍去負值,解得:

同理,
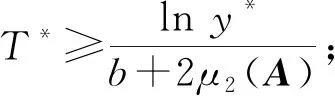
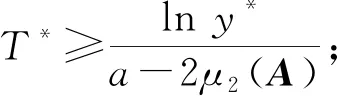
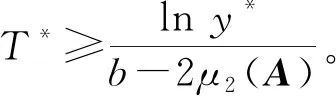
因為S3>0且y*>1,所以有T*>0。
易知,T*由僅與系統參數矩陣、增益矩陣、由拓撲確定的矩陣H、常數β有關。
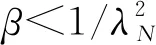
證明設
(16)
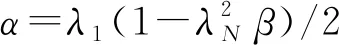

dV(t)=LV(t)dt+
ej(t)-ei(t)]-di(δi(t)+ei(t))}+
δT(t)(IN×N?(ATP+PA+CTPC)-
H?2PBBTP)δ(t)-
δT(t)(H?2PBTBP)e(t)≤
δT(t)(IN×N?(ATP+PA+CTPC)-
H?2PBBTP)δ(t)+
δT(t)(H?PBBTP)δ(t)+
eT(t)(H?PBBTP)e(t)≤
δT(t)(IN×N?(ATP+PA+CTPC)-
H?PBBTP))δ(t)+
λNeT(t)(IN×N?PBBTP)e(t)
(17)
由(5)式、(6)式與引理1易知λ(t)≥0。
設S(t)=V(t)+λ(t),由(6)式、(7)式、(17)式可得:
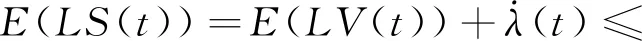
E(δT(t)(IN×N?(ATP+PA+CTPC)-
H?PBBTP))δ(t)+
βλNδT(t)(HH?PBBTP)δ(t)-σλ(t)≤
E(δT(t)(IN×N?(ATP+PA+CTPC)-
H?PBBTP))δ(t)+
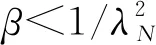
E(LS(t))≤E(δT(t)|IN×N?
CTPC)δ(t))-σλ(t)≤
-E(δT(t)δ(t))-σλ(t)≤
-E(δT(t)δ(t))
(18)
而
對?t∈[t0,+∞),有
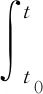
(19)
由引理4可得:
(20)
顯然
且帶領導者的系統可達均方一致。
由引理6及(5)式、(6)式、(10)式、(11)式可知,對?t∈[tk,+∞),若
E(‖(IN×N?K)e(t)‖2)-
βE(‖(H?K)δ(t)‖2)-λ(t)=0
存在解t1,則有t1-tk≥T*。
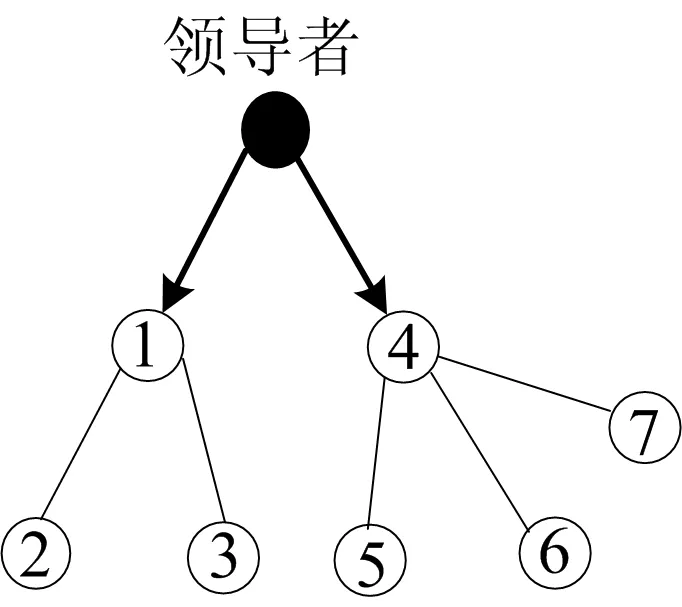
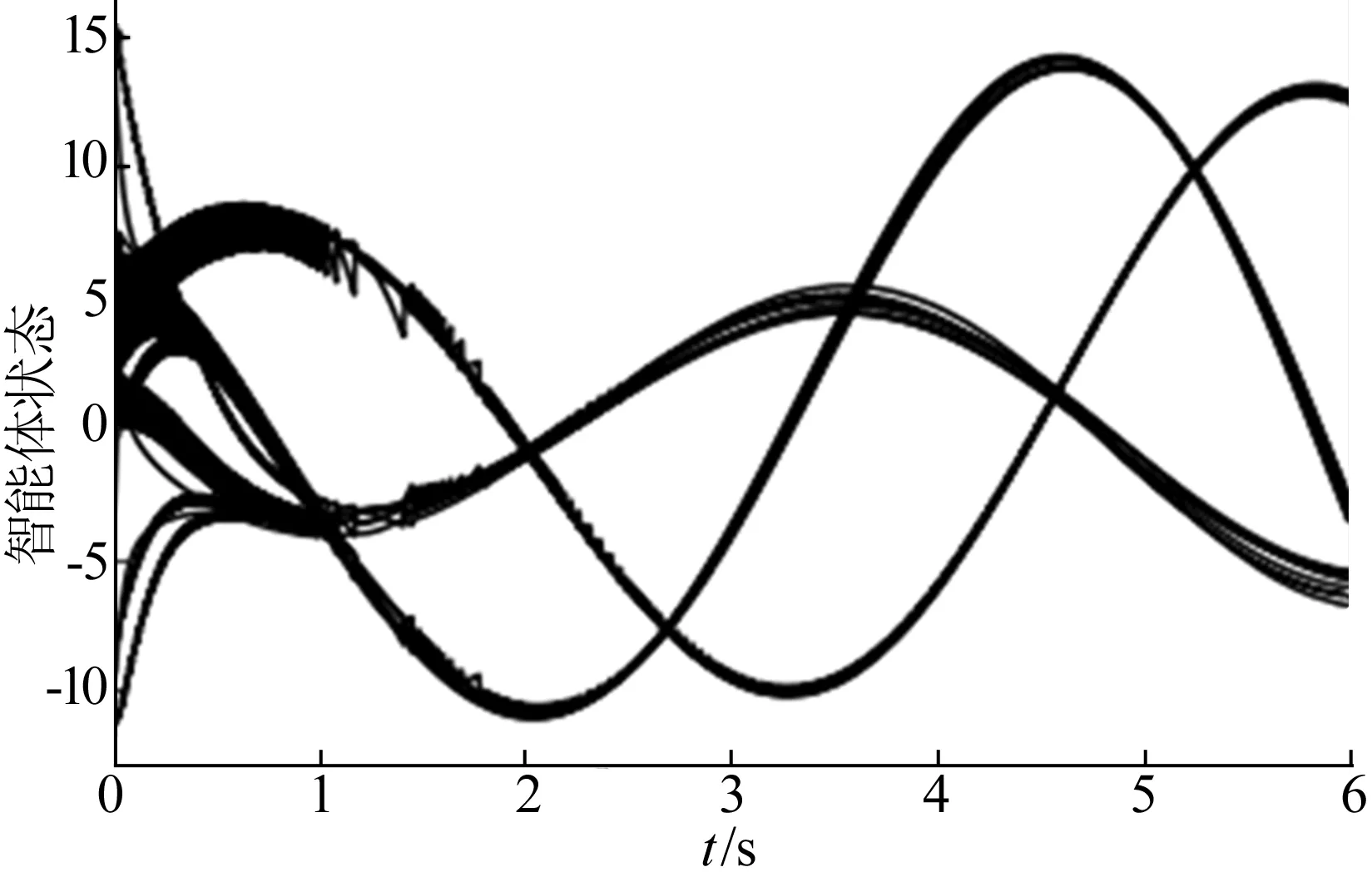
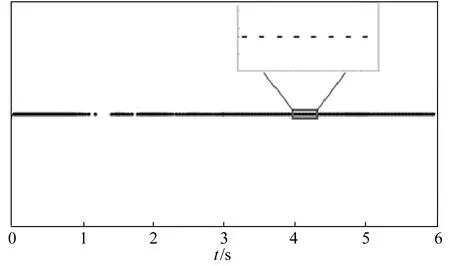
假設在上述事件驅動下,存在k,使得tk+1-tk=τk 由(15)式可知,f(T)為單調遞增函數且f(T*)=0,因此 Γ1(δ(tk),τk)-βΓ2(δ(tk),τk)<0。 若事件驅動在tk+1時觸發,λ(tk+1)>0,則 0=E(‖(IN×N?K)e(tk+1)‖2)- βE(‖(H?K)δ(tk+1)‖2)- λ(tk+1)≤Γ1(δ(tk),τk)- βΓ2(δ(tk),τk)-λ(tk+1) ≤ Γ1(δ(tk),τk)-βΓ2(δ(tk),τk)<0。 矛盾! 因此在上述事件驅動控制下,任意2個時間驅動觸發時刻間的時間間隔不會小于T*,故系統無芝諾行為發生。 考慮帶領導者的多智能體系統如下: 考慮有1個領導者7個跟隨者的有向圖,將領導者的所有跟隨者分屬于2個聯通子圖,如圖1所示。 每個聯通子圖可自領導者處獲取信息。 圖1 有領導者及2個聯通子圖的有向圖 取β=0.03,求得滿足定理1要求的增益矩陣為: 取σ=1,做仿真模擬,如圖2、圖3所示。可見系統趨同效果良好。 事件驅動觸發時刻圖如圖4所示。在該事件驅動下,系統多智能體間通訊次數為545次,較之連續通訊600 00次,可節省大量通訊資源,且最小事件間隔為0.002 8,無芝諾行為發生,見表1所列。 圖2 智能體狀態趨同效果圖 圖4 事件觸發時刻圖 表1 事件觸發次數與時間間隔 本文基于事件驅動方法對有乘性噪聲的線性對多智能體系統的均方一致性進行了研究,利用隨機分析和微分方程穩定性理論方法證明了帶領導者的線性隨機多智能體系統在該控制策略下可達均方一致,并證明了該事件觸發方案能夠避免芝諾行為的發生。最后通過仿真,驗證了該事件觸發方案可有效減少多智能體間通訊次數,避免芝諾行為。3 數值模擬
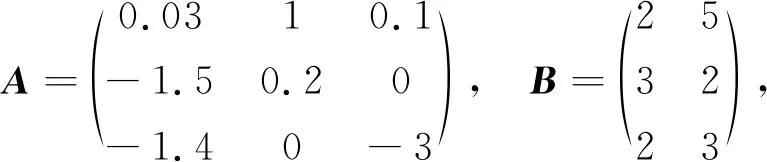

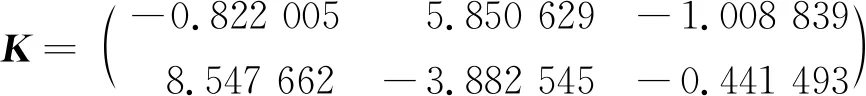

4 結 論

