霍爾天平材料的多場調控*

張靜言 竇鵬偉 趙云馳 張石磊 劉佳強 祁杰 呂浩昌劉若洋 于廣華 姜勇 沈保根 王守國?

1) (北京科技大學材料科學與工程學院, 北京材料基因工程高精尖創新中心, 北京 100083)

2) (中國科學院物理研究所, 磁學國家重點實驗室, 北京 100190)

3) (上海科技大學物質科學與技術學院, 上海 201210)

霍爾天平材料中層間耦合作用易于調控, 基于此可以實現多組態磁存儲模式, 其區別于當前基于自旋閥或者磁性隧道結的傳統二組態磁存儲原理.與此同時, 還可以在存儲單元中實現信息的邏輯運算從而提高器件整體的運算效率.這一設計有利于自旋電子學器件的微型化、集成化, 有望從物理原理上解決當前基于自旋閥或者磁性隧道結的傳統二組態自旋電子學材料器件的技術瓶頸, 進一步提高磁存儲密度, 為推動新型自旋電子學材料的研究開辟了一條新的研究思路.首先, 本綜述將介紹基于霍爾天平材料的磁存儲器件的研究背景; 其次, 重點介紹霍爾天平存儲邏輯器件一體化設計的提出與發展歷程; 再次, 介紹霍爾天平材料關鍵指標—霍爾電阻比值的界面調控及物理機理探索; 隨后詳細闡述霍爾天平體系中磁性斯格明子的產生與多場調控等動態行為.最后, 簡單介紹霍爾天平結構在其他相關材料中的擴展、應用, 并展望其在未來器件應用中的前景.

1 引 言

20 世紀中葉, 以操控電子電荷屬性為基礎的傳統微電子技術取得了飛速發展, 為人類的生活帶來了極大便利.隨著人類對產品性能的要求越來越高, 對于微電子產品而言, 由于晶體管數量的不斷增加而帶來的散熱、兼容等一系列的問題, 使得微電子技術的發展受到了嚴重的制約[1].為了解決上述瓶頸和挑戰, 科學家們始終孜孜不倦地探索新材料、新原理和新技術, 在嘗試優化結構和改進工藝的同時也在尋求利用新材料中的新奇物理效應來實現信息技術的革新.

自旋電子學作為凝聚態物理學與材料科學及微電子技術的新興交叉學科, 伴隨著巨磁電阻效應(GMR)的發現成為近代磁學的里程碑, 揭開了人類利用電子自旋這一電子所具有的另一個本征屬性來進行信息存儲和讀寫的序幕[2].隨著材料制備和微納米加工技術的日益成熟, 更多新型功能材料及器件被設計和制備出來, 為科學家們深入研究其中的物理機理提供了良好的基礎.過去20 多年中, 自旋電子學材料、物理及相關器件的研究得到了突飛猛進的發展, 極大地推動了信息產業的變革式發展, 尤其是磁存儲密度的量級提升[3?5].以信息存儲產業需求為先導, 進一步降低器件尺寸和提高磁信息存儲密度是科學家們普遍關注的熱點問題之一.科學家們首先利用兩組態的GMR[6]、隧穿磁電阻(TMR)[7]自旋電子學材料, 通過降低其單元尺寸和減少薄膜厚度來提高這類器件的存儲密度等物理性能指標.經過十余年的基礎研究, 基于TMR 的磁性隧道結(MTJ)作為磁隨機存儲器單元得到了迅速發展.特別是, 利用自旋轉移矩[8]可以實現MTJ 磁化翻轉, 加速其作為磁隨機存儲器單元的實用化進程, 解決磁場誘導MTJ 磁化翻轉中磁場難以微型化的技術瓶頸.隨著研究的不斷深入, 科學家們也逐步嘗試利用新的物理效應[9](例如自旋軌道矩(SOT))推動TMR 存儲器件的繼續發展.與此同時, 隨著TMR 材料制備工藝的不斷成熟, 基于TMR 的自旋電子學器件也逐步進入大規模信息存儲產業中并得到實際應用.需要指出的是, 科學家們發現當磁性器件的尺寸降低到一定程度時(如納米級別), 量子尺寸效應和熱效應使得存儲單元無法長時間正常工作甚至失效, 這讓數據保存的時間大幅度縮短, 數據穩定性也隨之降低.隨著對自旋電子學器件微型化、集成化的需求不斷提高, 以GMR 和TMR 效應為基礎的二組態自旋電子學材料遇到了前所未有的技術瓶頸, 受到了摩爾定律和超順磁極限的嚴重制約.與此同時, 過去數十年中科學家們為了優化提高磁存儲單元的核心指標—磁電阻比值而嘔心瀝血, 但是在磁電阻比值經歷了一段快速提升過程, 室溫下達到604%之后, 便無法進一步提升.此外, TMR 的最高比值仍未達到理論預期值[10?12], 且與半導體二極管的開關比存在一定程度的差距, 這也為磁信息存儲的進一步發展蒙上一層陰影.

從應用的角度來看, 國家集成電路長遠規劃(2019—2026 年)的藍圖中, 高集成密度(3D (three dimensional)存儲模式)、低能耗和高運算效率的電路模式將占據最高的優先級并成為產業化和商業化的首選.雖然科學家們也在不斷探索利用多場調控等手段提高信息磁存儲關鍵性指標, 優化原有的二組態磁存儲構架[13?17], 但是仍無法完美地彌補二組態的固有短板.為了從根本上突破這一技術瓶頸, 適應未來信息產業發展的需要, 人們將研究的重點集中在新型自旋電子學材料的設計和基礎物理問題的探索上.目前, 主要的研究方向集中在兩條主線上: 1)繼續探索新型磁性功能材料和具有新自旋結構的材料體系(例如基于疇壁運動的賽道存儲器[18]、磁性斯格明子[19]等), 優化二組態存儲模式, 提高存儲密度; 2)突破傳統二組態存儲模式, 尋找具有空間多組態存儲的新結構、新材料從而實現3D 存儲模式[20].基于這兩大主要研究方向, 科學家們做出了大量原創性的理論和實驗工作, 并在物理原理、材料設計和器件加工等多方面取得了重要性突破, 一系列研究成果將進一步促進自旋電子學的蓬勃發展, 同時為實現高密度新型信息磁存儲奠定堅實基礎.其中, 霍爾天平是利用垂直磁性多層膜材料的反常霍爾效應所設計的新型自旋電子學材料, 其核心為垂直鐵磁層/隔離層/垂直鐵磁層所構成的三明治結構.接下來, 本文將重點介紹近期霍爾天平材料在新型信息存儲器件中的現狀、應用和未來可能的發展方向.

2 基于霍爾天平結構的信息磁存儲邏輯器件的提出

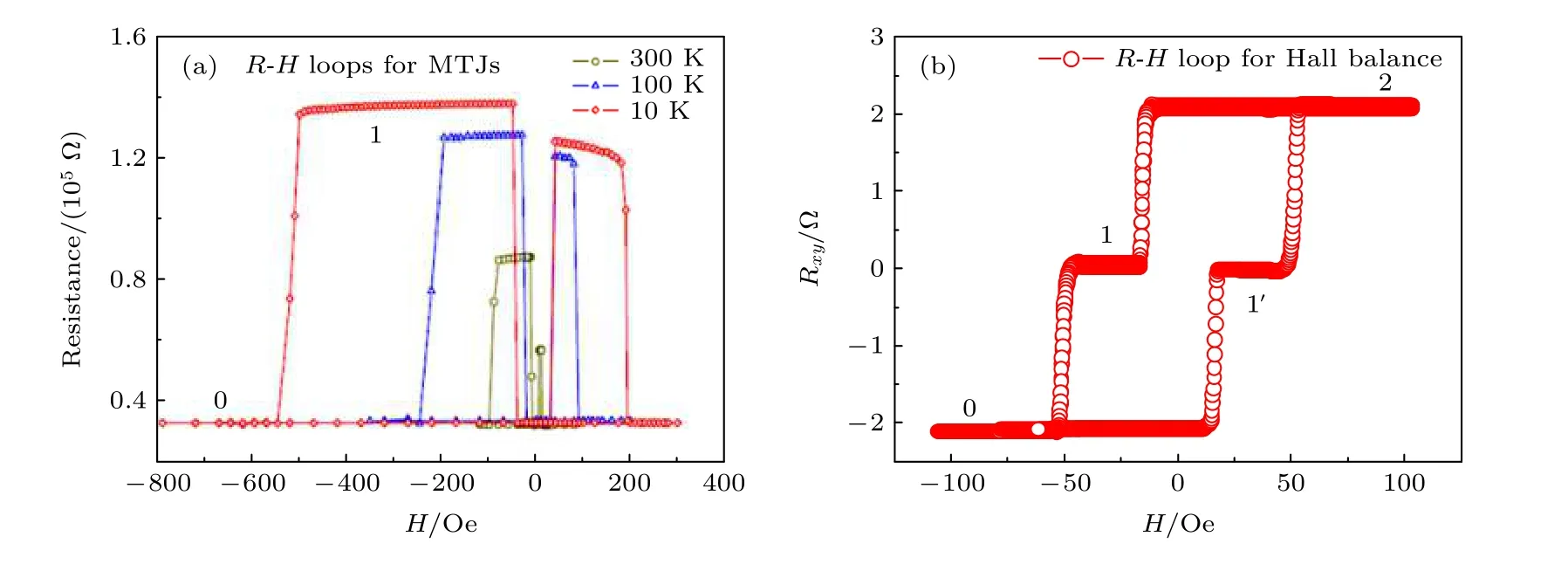
圖1 (a)磁性隧道結Fe(25)/MgO(3)/Fe(10)/IrMn(10) (厚度單位均為納米)中的R-H 輸出曲線[21]; (b)霍爾天平CoO(10)/[Co(0.3)/Pt(1)]3/NiO(1.1)/Pt(0.6)/[Co(0.3)/Pt(1)]3/CoO(10) (厚度單位均為納米)中的R-H 輸出曲線Fig.1.(a) R-H loops for the magnetic tunnel junction with the structure of Fe(25)/MgO(3)/Fe(10)/IrMn(10) (in nm)[21]; (b) R-H loop for Hall balance with the structure of CoO(10)/[Co(0.3)/Pt(1)]3/NiO(1.1)/Pt(0.6)/[Co(0.3)/Pt(1)]3/CoO(10) (in nm).

傳統磁信息存儲主要利用GMR 和TMR 效應等實現高、低二組態存儲模式(即“1”和“0”), 其核心單元是一個由兩層鐵磁薄膜和中間隔離層所組成的三明治結構.當隔離層為金屬薄膜時, 如Cu 和Cr, 體系具有GMR 效應; 而當隔離層為絕緣體時, 如Al2O3和MgO, 體系具有TMR 效應.通常兩種鐵磁性薄膜的矯頑力不同, 其中矯頑力低、容易翻轉的那一層稱為自由層; 另外一個磁性層的矯頑力較大, 在器件中常利用反鐵磁薄膜通過交換耦合原理對其進行釘扎來提高矯頑力, 被稱為釘扎層.上述三明治結構工作的物理原理是采用外加磁場、外加電流產生的奧斯特磁場、自旋極化電流等手段來控制磁性多層膜結構中自由層和釘扎層磁矩的相對取向.例如, 當兩層處于平行排列時,體系處于低電阻狀態; 當兩層處于反平行排列時,體系處于高電阻狀態.高低電阻狀態對應于信息存儲的“1”和“0”兩態, 如圖1(a)所示[21].從器件架構設計的角度來看, 如果要在基于GMR 和TMR 的信息存儲器件中實現多組態信息存儲, 那么一種可行的方法是增加鐵磁層的個數.基于這一思路, 人們嘗試通過設計雙勢壘隧道結器件以求實現多組態信息存儲[22].但是, 雙勢壘隧道結對磁性多層膜材料的制備和器件微納加工工藝提出了更高的要求, 特別是超薄鐵磁層的脫耦合和磁性層矯頑力的精確控制十分具有挑戰性.因此, 這方面的研究工作仍然任重而道遠.與此同時, 人們也在嘗試利用磁性功能薄膜中的新奇物理效應設計具有不同功能的高密度存儲材料及原理型器件.其中, 利用磁性多層膜中的反常霍爾效應制備具有高存儲密度的新型磁性存儲材料逐步受到了人們的關注, 其典型輸出曲線如圖1(b)所示.

反常霍爾效應是磁性材料所特有的一種超大霍爾效應, 由美國實驗物理學家Edwin Hall 于19世紀末在鐵磁金屬中首次觀測到.與圖2(a)所示的正常霍爾效應不同的是, 反常霍爾效應是一種自旋相關的物理效應, 具有不同自旋方向的載流子在自旋軌道耦合作用下向著相反的方向運動, 從而在垂直于外加電流方向的兩端積累并形成電勢差.圖2(b)是反常霍爾效應原理圖, 它是磁性材料所特有的不需要外加磁場就可以觀測的霍爾效應.但是, 利用外磁場等手段可以改變磁性材料的磁矩方向, 從而可以調控反常霍爾電壓的方向, 即磁矩向上(下)對應于反常霍爾電壓為正(負), 這就為利用反常霍爾效應來設計信息存儲器件提供了可能.

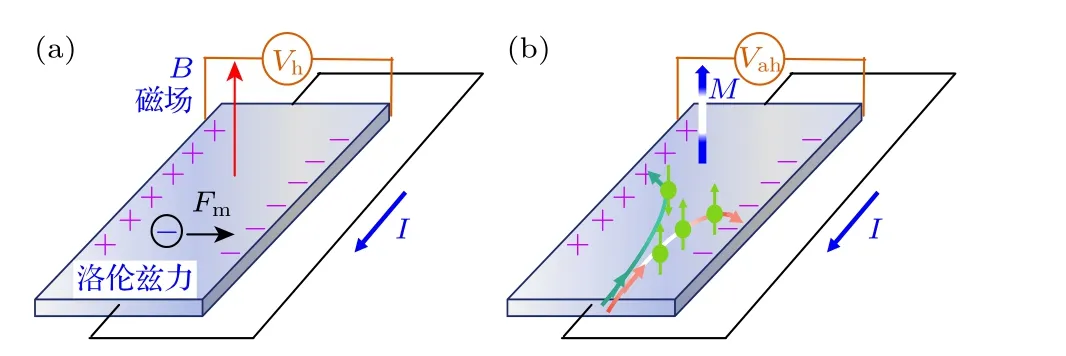
圖2 (a)正常霍爾效應和(b)反常霍爾效應原理圖Fig.2.Schematic of (a) ordinary Hall effect and (b) anomalous Hall effect.

通常情況下, 反常霍爾效應的大小不僅與磁性材料的磁化強度成正比, 還和磁性多層膜中的界面狀態息息相關, 這也為后續調控基于反常霍爾效應的自旋電子學器件性能提供了一條有效的途徑.早期的關于反常霍爾效應的研究主要集中在揭示其物理起源和內在機制上, 研究體系也相對單一, 主要發現了與自旋軌道耦合作用相關的內稟機制以及與雜質散射相關的外稟機制[23?26].近些年來, 隨著材料制備工藝的發展、微觀結構的精細表征以及理論計算方法的完善, 關于反常霍爾效應的研究體系也逐漸從單一鐵磁金屬體系擴展到稀磁半導體、稀土過渡金屬合金、鐵磁合金和磁性復合多層膜結構等[27?30].多元、復合的納米結構使得反常霍爾效應中不同的物理機理相互競爭, 其反常霍爾信號也受到了納米薄膜材料本身晶體結構、組分、微觀缺陷、界面結構等一系列因素的影響[31?38].隨著研究的進一步深入, 人們對于磁性多層膜中反常霍爾效應的物理起源和調控機理有了更加清晰的認知,這也為后續設計不同功能性的反常霍爾器件奠定了物理和材料基礎.基于前期大量的研究工作, 國內多個團隊先后利用超薄復合多層膜結構設計開發了具有高靈敏度的反常霍爾線性磁傳感器材料[39?41],為反常霍爾效應材料及器件設計拉開了帷幕.

近期, 一種新型多組態磁存儲材料概念—霍爾天平[42]被國內學者首次提出.霍爾天平的核心結構為鐵磁層1/隔離層/鐵磁層2 的三明治結構,其中鐵磁層1 和鐵磁層2 均具有垂直磁各向異性,且兩個鐵磁層之間具有較強的層間交換耦合作用.隔離層可以為絕緣材料(例如氧化鎳NiO, 氧化鎂MgO 等), 也可以為金屬材料(例如釕Ru, 鉑Pt,銅Cu, 鉭Ta 等).霍爾天平可以具有多種狀態: 反向平行、反平行和正向平行, 如圖1(b)中所示的“0”, “1”, “1′”和“2”狀態.與基于GMR 和TMR效應的二組態信息存儲器件不同的是, 霍爾天平可以有效地區分磁矩平行的兩種狀態, 即正向平行態和反向平行態.以圖3(a)中基于NiO 隔離層的霍爾天平為例[42], 該體系的霍爾電阻輸出曲線顯示了三個穩定的狀態: 1)兩個磁性層的磁矩處于正向平行時, 反常霍爾電壓等于他們各自的反常霍爾電壓之和, 稱為高阻態; 2)兩個磁性層的磁矩在低場下處于反平行狀態, 體系的反常霍爾電壓等于兩者反常霍爾電壓之差, 如果兩個磁性層的反常霍爾效應大小完全相同, 那么此時的總霍爾電壓為零,即中間阻態; 3)當兩個磁性層的磁矩處于反向平行時, 反常霍爾電壓等于兩者的反常霍爾電壓之和, 大小與正向平行時的數值相同, 卻具有相反的方向, 此時為低阻態.利用霍爾天平設計的新型自旋電子學器件可以實現三組態甚至多組態, 進而實現高密度3D 信息存儲陣列, 如圖3(b)所示[42].這就為新型高密度3D 存儲模式提供了有效的途徑,為后續的多功能磁存儲材料及相關器件設計提供了可能的發展方向.

利用霍爾天平進行信息存儲的同時, 科研工作者也嘗試在單一霍爾天平存儲單元內實現信息布爾邏輯運算, 從根本上解決信息存儲和邏輯運算分離的限制, 從而實現可編程的存算一體化器件設計.對于大多數可編程的邏輯運算而言, 邏輯操作均需要在實際運算發生前對基本的布爾邏輯進行預選擇, 這將極大地限制信息運算處理的速度.為了實現可編程的邏輯門計算操作, 研究者首先設計了一種結構簡單的霍爾天平存儲器件[42], 其核心結構為兩層具有垂直磁各向異性的[Co/Pt]n多層膜, 中間用超薄的NiO 隔離層隔開, 通過材料結構的優化, 最終實現了具有穩定三組態的對稱霍爾電壓輸出曲線.在此基礎上進行了可編程的邏輯門運算操作.

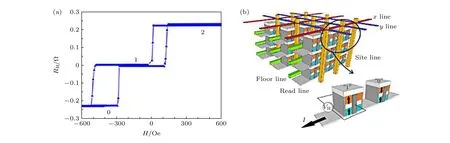
圖3 (a)基于NiO 的霍爾天平R-H 曲線; (b)基于霍爾天平的3D 存儲陣列示意圖[42]Fig.3.(a) R-H loop for Hall balance based on NiO spacer; (b) schematic of 3D storage based on Hall balance[42].

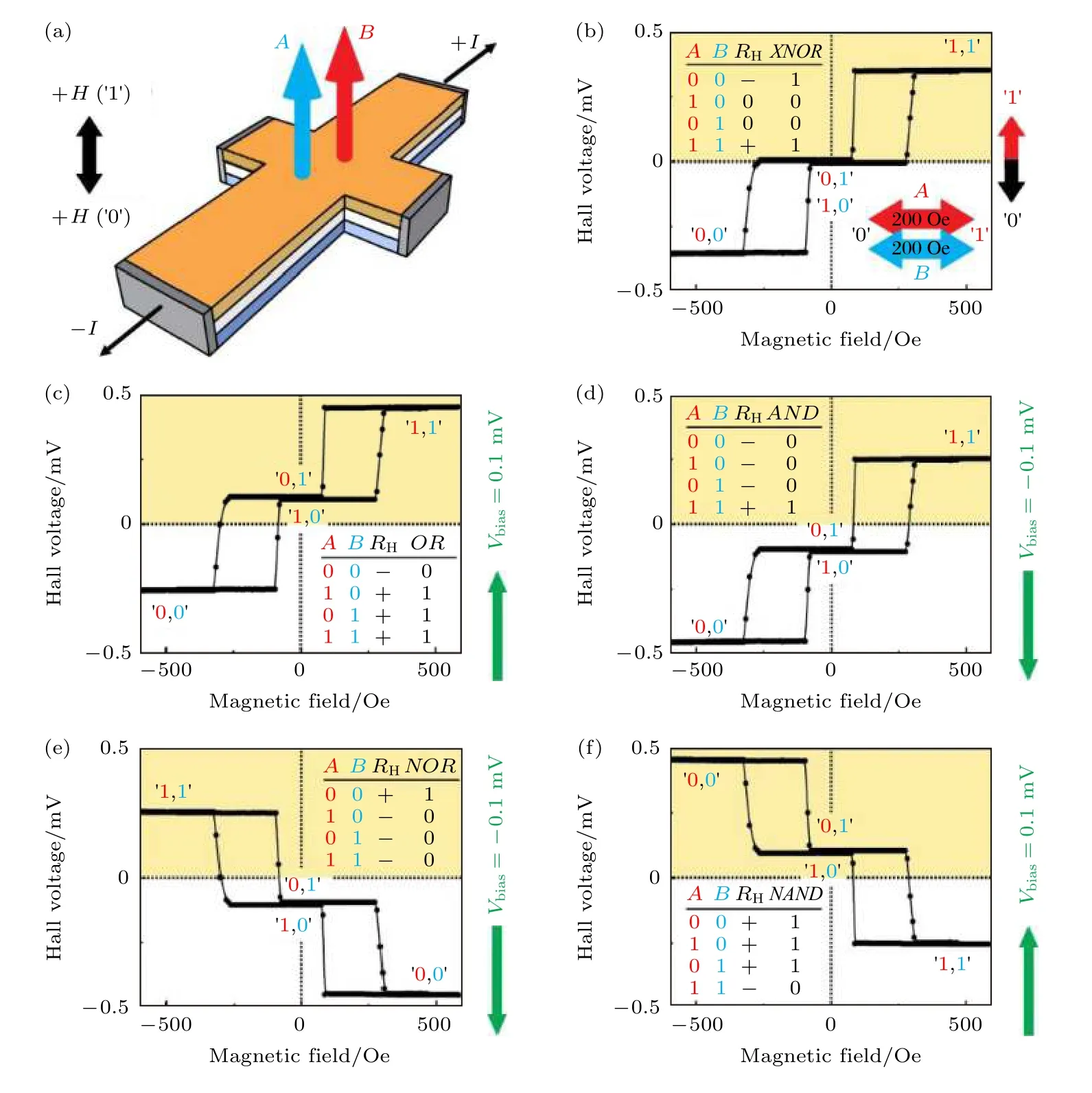
圖4 基于霍爾天平存儲單元的基本布爾邏輯運算輸出曲線及真值表[42]Fig.4.Boolean logic operation in storage cell based on Hall balance and truth table [42].

圖4 給出了單一霍爾天平存儲單元進行可編程布爾邏輯門運算操作[42].對于一個具有三組態的霍爾天平器件單元而言, 經過簡單操作輸出三元代碼就可以實現所有的布爾邏輯運算.為了實現多種可編程的基本布爾邏輯運算, 選取兩個垂直于薄膜表面的磁場A 和B (也可以采用兩個電流IA和IB產生的磁場)作為輸入值, 反常霍爾電壓(V)作為輸出值, 如圖4(a)所示.對于輸入值磁場A 和B而言, 預先設定正向磁場(負向磁場)為邏輯輸入值1(0).需要注意的是, 磁場A 和B 幅值相等, 且單個磁場(A 或者B)無法實現薄膜磁矩的翻轉.例如, 對于結構優化后的三組態霍爾天平而言, 磁場A 和B 幅值均為200 Oe; 同時設定霍爾電壓作為輸出值.只有當磁場A 和B 同向時, 才能實現薄膜磁矩的翻轉, 即A, B = (0, 0), (1, 1)分別對應于霍爾天平中的“↓↓”, “↑↑”狀態, 電壓絕對值為最大值, 即輸出值記為1.對于磁場A 和B 反向時, 其輸入值為(0, 1)和(1, 0), 對應霍爾天平中的“↓↑”或“↑↓”狀態, 即霍爾電壓絕對值接近零, 即輸出值記為0.基于上述的操作關系, 單一霍爾天平存儲單元中可以實現XNOR 邏輯門運算,即當輸入值A 和B 相同對應輸出值為1, 反之輸出值為0, 具體真值表如圖4(b)所示.

為了在同一霍爾天平單元內實現可編程的邏輯門運算, 可以引入兩個輔助操作變量, 即霍爾天平器件中的縱向電流方向(沿著霍爾條的方向)和橫向偏置電壓方向(膜面內沿著垂直于縱向電流方向), 如圖4(c)—圖4(f)所示.在圖4(b)的霍爾電壓輸出曲線基礎上, 橫向偏置電壓的引入使得霍爾電壓輸出曲線將偏離X 軸, 如圖4(c)和圖4(d)所示.此時, 霍爾電壓為正(負)值對應于邏輯門輸出值的1(0).圖4(c)給出了利用霍爾天平結構實現OR 邏輯門運算.當磁場A 和B 均為負值(輸入值為(0, 0)), 此時對應于霍爾電壓為負值(輸出值為0);當磁場A 和B 不同號(輸入值為(1, 0)或者(0, 1)),由于正的橫向偏置電壓的存在, 對應于霍爾電壓為正值(輸出值為1); 當磁場A 和B 均為正值(輸入值為(1, 1)), 對應于霍爾電壓為正值(輸出值為1).因此, 利用霍爾天平就可以實現OR 邏輯門運算操作.此外, 利用負的橫向偏置電壓可以在同一霍爾天平單元中實現AND 邏輯門運算操作, 如圖4(d)所示.接下來在圖4(c)和圖4(d)的基礎上, 可以將縱向電流的方向從正向變為負向, 同時改變橫向偏置電壓的方向, 那么霍爾天平的輸出響應曲線分別如圖4(e)和圖4(f)所示.圖4(e)和圖4(f)中的真值表顯示該器件還可以分別實現NOR 和NAND邏輯門運算操作.根據上述結果可知, 利用單一霍爾天平存儲單元可以進行基本的布爾邏輯運算, 進而實現可編程的邏輯操作.

因此, 利用霍爾天平單元不僅實現了多組態信息磁存儲, 還可以完成存算一體化設計.基于霍爾天平結構的磁存儲邏輯計算一體化器件突破了當前自旋電子學領域的技術瓶頸, 給出了一種解決當前磁隨機存儲器所面臨問題的有效途徑, 符合未來3D 存儲模式的發展需求[42,43].此外, 基于這種具有兩個鐵磁層的霍爾天平器件的設計理念, 一種多組態存儲材料—自旋算盤[44]也被科研工作者提出, 并且相應的原理型器件也被成功制備出來.科研工作者受到中國古代算盤技術思想的啟發, 設計了一種多磁性層的薄膜材料, 利用材料中各個磁性層磁矩逐層翻轉, 從而實現了多進制計數的功能, 如圖5所示[44].隨后, 科研人員通過對NiO 和[Co/Pt]n多層膜之間的界面耦合和層間耦合作用的精確調控, 實現了外磁場驅動下磁性層磁矩逐層翻轉, 從而實現了多組態信息磁存儲, 極大地拓展了存儲器件的單位存儲密度.

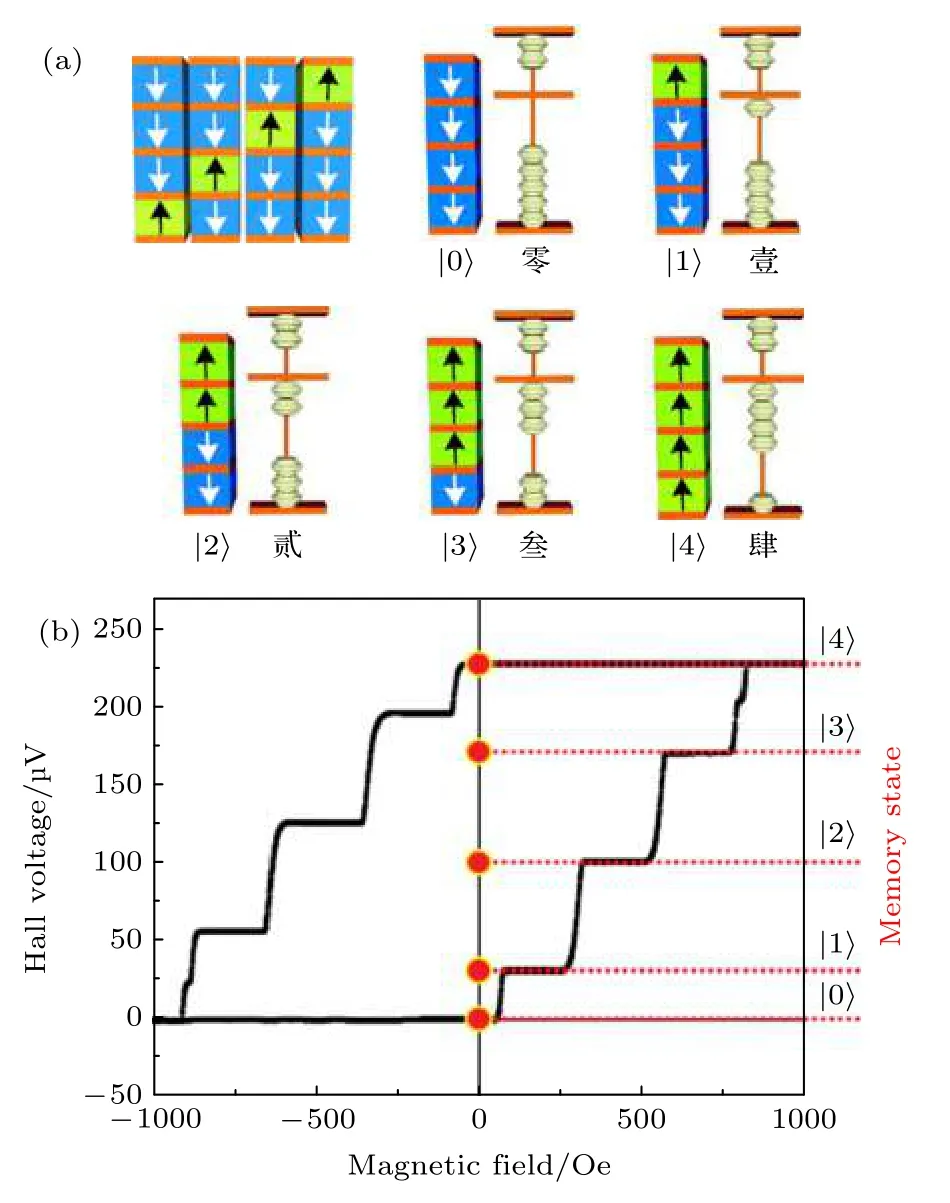
圖5 (a)自旋算盤設計示意圖; (b)基于NiO 隔離層的自旋算盤霍爾輸出曲線[44]Fig.5.(a) Schematic of magnetic abacus memory; (b) Hall loop for the magnetic abacus based on NiO spacer[44].

3 霍爾天平中霍爾電阻比值的調控

正如前文所述, GMR 和TMR 比值分別是自旋閥和磁性隧道結的核心指標, 其數值大小影響著以自旋閥或者隧道結為信息存儲單元的綜合性能,尤其是靈敏度和信噪比.以TMR 效應為例, 目前室溫下MR 比值(如CoFeB/MgO/CoFeB 磁性隧道結)最高值可達604%, 低溫下高達1144%[10], 且近十余年來該比值沒有進一步提高.受限于材料制備技術和物理原理的內在限制, 隧道結中TMR 比值的量級仍無法與半導體二極管的開關比相媲美.鑒于這一現狀, 科學家們在霍爾天平結構的磁性多層膜中提出了霍爾電阻比值這一指標[42].霍爾電阻比值(Hall resistance ratio, HRR)是霍爾天平材料及器件的核心關鍵指標, 代表了霍爾天平結構中的磁電阻開關比, 其表達式為

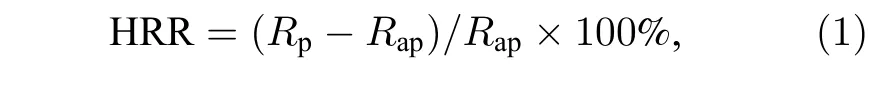
其中Rp和Rap分別代表正向平行態霍爾電阻和反平行態霍爾電阻.

通常情況下, HRR 主要受到兩方面因素的影響: 1)霍爾天平的組態數; 2)霍爾天平中各組態電阻的大小.對于一個僅具有兩組態的霍爾天平磁性多層膜而言, 體系不具備HRR 值; 只有當霍爾天平具有多組態時, 衡量體系的HRR 比值才具有物理涵義.此外, HRR 值的大小由Rp和Rap兩部分決定, 其中Rp和Rap取決于霍爾天平中兩個鐵磁層的反常霍爾效應的大小.通常情況下, 為了獲得更高的HRR 值, 可以采用降低Rap同時提高Rp的方法來實現.研究發現: 磁性多層膜中的自旋輸運性質不僅與鐵磁層本身的磁化強度有關, 同時還受到磁性層間耦合作用、界面化學狀態、界面粗糙度、鐵磁層的晶化程度以及界面缺陷濃度等多方面的影響[41,45?47].因此, 深入研究并澄清磁性多層膜材料設計對霍爾天平HRR 效應調控內在機理, 實現高HRR 值的霍爾天平材料及器件制備是當前亟待解決的熱點問題之一.

首先, 采用超高真空多靶磁控濺射鍍膜系統制備了以鐵磁層/氧化物/鐵磁層([Co/Pt]n/oxide spacer/[Co/Pt]n)為核心結構的霍爾天平材料.核心鐵磁層選用[Co/Pt]n多層膜, 主要是由于[Co/Pt]n多層膜具有較強的自旋軌道耦合作用和易于調控的垂直磁各向異性(PMA); 氧化物選擇磁性隧道結中常用的MgO 作為隔離層, 其具有一定的晶體結構, 易于調控磁性薄膜的層間耦合.圖6(a)給出了樣品[Co/Pt]n/MgO/[Co/Pt]n的霍爾輸出曲線[42].從霍爾輸出曲線不難看出, 該樣品的兩個垂直磁性層的磁化方向是分步翻轉的, 具有明顯的多組態特性.樣品的Rp和Rap分別為650 和70 mΩ, 其HRR值達到850%, 該數值高出了目前報道的TMR 室溫下最高值[10].在此基礎上, 科學家嘗試利用NiO作為隔離層, 經過材料結構優化, 成功制備出結構為NiO/[Co/Pt]n/NiO/[Co/Pt]n的霍爾天平, Rp和Rap分別為630 和2 mΩ, 其HRR 值達到31400%,如圖6(b)所示[42].

圖6 (a)樣 品NiO(20)/[Co(0.4)/Pt(1.2)]/MgO/[Co(0.4)/Pt(1.2)]/NiO(1) (nm)的霍爾輸出曲線; (b)樣品NiO(50)/Pt(0.6)/[Co(0.3)/Pt(1)]/NiO/[Co(0.4)/Pt(1.2)] (單位: nm)的霍爾輸出曲線[42]Fig.6.(a) Hall loop for the sample NiO(20)/[Co(0.4)/Pt(1.2)]/MgO/[Co(0.4)/Pt(1.2)]/NiO(1) (in nm); (b) Hall loop for the sample NiO(50)/Pt(0.6)/[Co(0.3)/Pt(1)]/NiO/[Co(0.4)/Pt(1.2)] (in nm) [42].

以NiO 作為隔離層的霍爾天平為基礎, 科學家們進一步對材料進行結構優化, 重點研究了鐵磁層、隔離層對HRR 的調控作用.圖7(a)—圖7(c)給出了不同NiO 厚度(tNiO)的霍爾天平Pt(0.6)/[Co(0.4)/Pt(1)]3/Co(0.4)/Pt(0.3)/NiO(tNiO)/Pt(0.3)/[Co(0.4)/Pt(1)]4(厚度單位為納米)的霍爾輸出曲線[48].從圖中可以看出, 兩個[Co/Pt]n多層膜的耦合狀態強烈地依賴于NiO 層厚度, 例如, 當tNiO=1 nm 或者1.1 nm 時, 霍爾天平中的鐵磁層處于反鐵磁耦合狀態.此時, 霍爾天平具有多個組態: 1)鐵磁層的磁矩方向反平行排列對應于中間阻態(如圖中狀態“1”或者“1'”), 狀態“1”或者“1'”的出現是由反鐵磁耦合作用強度和鐵磁層/氧化物界面結構共同決定的; 2)鐵磁層的磁矩方向正向平行和反向平行分別對應于高阻態和低阻態(如圖中狀態“2”和“0”).根據前面的霍爾天平中HRR 值的計算公式可知, 圖7(a)和圖7(b)中霍爾天平HRR值分別為1122%和1089%.繼續增加NiO 層厚度至1.2 nm 時, 霍爾天平的兩個鐵磁層變成鐵磁耦合狀態, 如圖7(c)所示.對于鐵磁耦合的霍爾天平而言, 兩個鐵磁層的磁矩將一致翻轉, 那么就沒有中間狀態, 因此就沒有HRR 值.在圖7(d)的基礎上改變上層鐵磁多層膜[Co/Pt]n中Pt 的厚度(tPt),制備出結構為Pt(0.6)/[Co(0.4)/Pt(1)]3/Co(0.4)/Pt(0.3)/NiO(1.1)/Pt(0.3)/[Co(0.4)/Pt(tPt)]4(厚度單位均為納米)的樣品, 其霍爾輸出曲線如圖7(d)—圖7(f)所示.隨著上層[Co/Pt]n多層膜中tPt降低, 該結構的霍爾天平中兩個鐵磁層始終保持著反鐵磁耦合狀態.當tPt= 0.8 nm 時, 霍爾天平中的“1”或者“1'”對應的電阻值基本相同, 所以霍爾天平形成穩定的三組態.此時, 霍爾天平的Rp和Rap分別為1050 和6 mΩ, 其HRR 值達到17400%.上述結果表明, 改變霍爾天平中的鐵磁層和隔離層的厚度可以有效地調控阻態的個數和HRR 比值, 這主要是由霍爾天平的耦合狀態強烈依賴于材料結構所導致的.

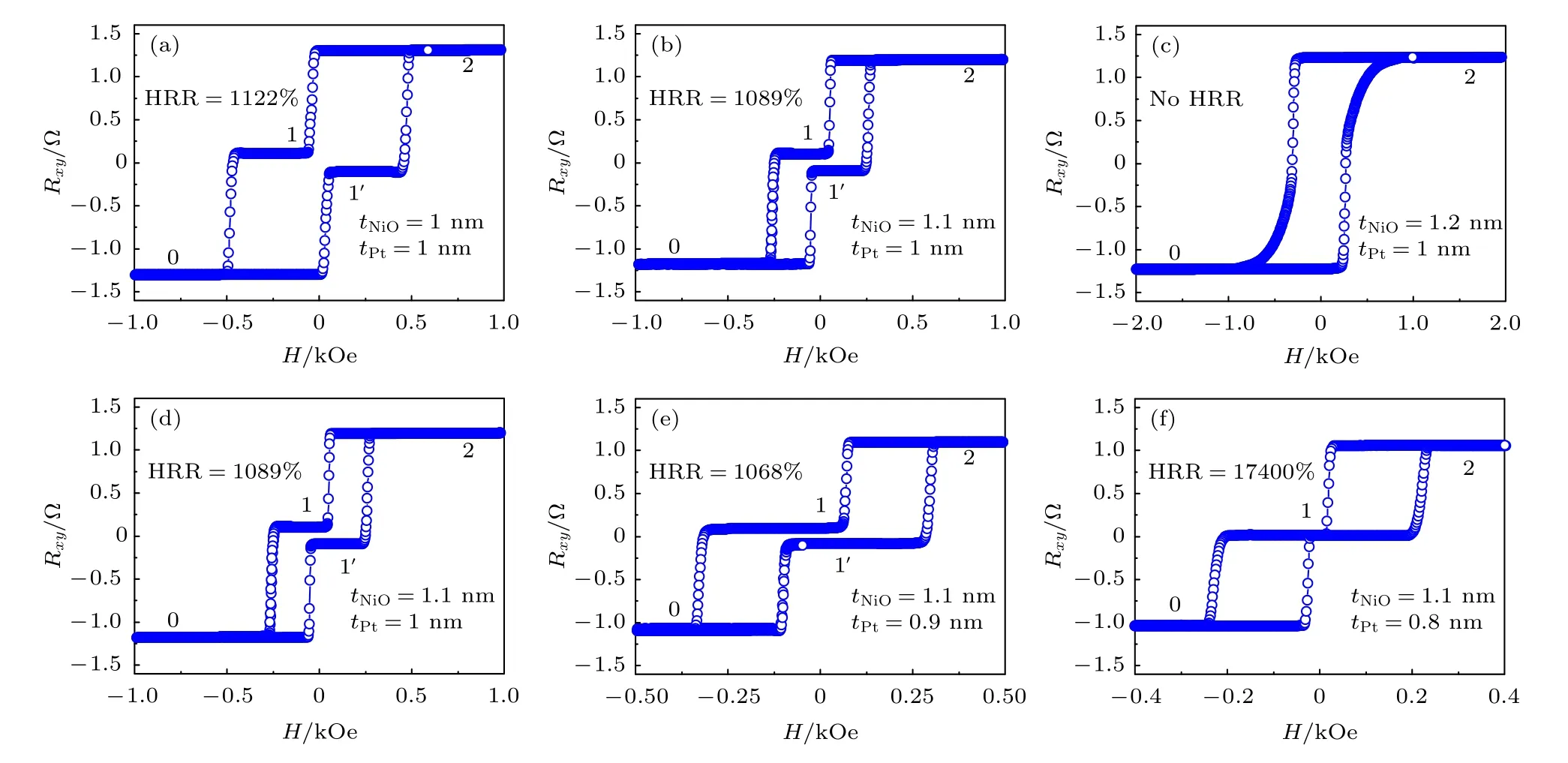
圖7 (a)?(c)樣品Pt(0.6)/[Co(0.4)/Pt(1)]3/Co(0.4)/Pt(0.3)/NiO(tNiO)/Pt(0.3)/[Co(0.4)/Pt(1)]4 (厚度單位為納米)的霍爾曲線;(d)?(f)樣品Pt(0.6)/[Co(0.4)/Pt(1)]3/Co(0.4)/Pt(0.3)/NiO(1.1)/Pt(0.3)/[Co(0.4)/Pt(tPt)]4 (厚度單位均為納米)樣品的霍爾輸出曲線[48]Fig.7.(a)?(c) Hall loops for the sample Pt(0.6)/[Co(0.4)/Pt(1)]3/Co(0.4)/Pt(0.3)/NiO(tNiO)/Pt(0.3)/[Co(0.4)/Pt(1)]4 (in nm);(d)?(f) Hall loops for the sample Pt(0.6)/[Co(0.4)/Pt(1)]3/Co(0.4)/Pt(0.3)/NiO(1.1)/Pt(0.3)/[Co(0.4)/Pt(tPt)]4 (in nm)[48].

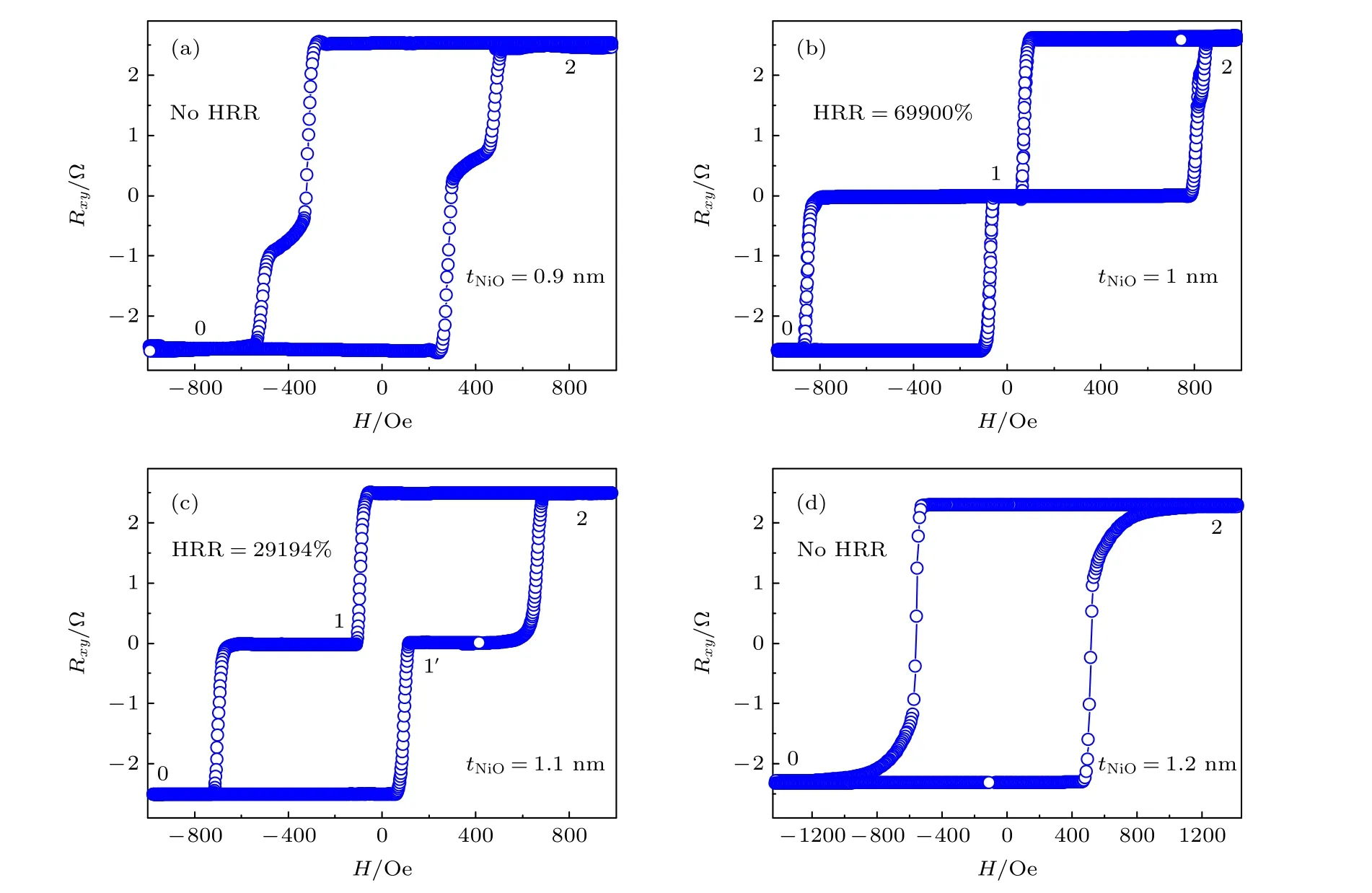
圖8 (a)?(d)樣品CoO(3)/[Pt(0.6)/Co(0.4)]4/Pt(0.3)/NiO(tNiO)/[Co(0.4)/Pt(0.6)]4/CoO(3)(厚度單位為納米)的霍爾回線[48]Fig.8.(a)?(d) Hall loops for the sample CoO(3)/[Pt(0.6)/Co(0.4)]4/Pt(0.3)/NiO(tNiO)/[Co(0.4)/Pt(0.6)]4/CoO(3) (in nm)[48].

利用金屬/氧化物界面工程設計可以提高載流子的自旋相關散射進而提高Rp值, 為進一步優化霍爾天平的HRR 比值提供了一條有效的途徑.以上述樣品結構為基礎, 在霍爾天平核心結構的兩側引入CoO/[Co/Pt]n和[Co/Pt]n/CoO 界面, 研究其相關物性.這里需要特別說明的是: 考慮到CoO層的引入會提高CoO 和[Co/Pt]n之間的界面耦合作用, 從而會影響到霍爾天平的磁性層間耦合狀態.因此, 在引入CoO 的同時還需要對[Co/Pt]n多層膜的厚度進行細微調制.圖8(a)—圖8(d)是結構為CoO(3)/[Pt(0.6)/Co(0.4)]4/Pt(0.3)/NiO(tNiO)/[Co(0.4)/Pt(0.6)]4/CoO(3)(厚度單位為納米)霍爾天平的霍爾輸出回線[48].從圖中可以看出, 隨著NiO 層厚度的增加, 霍爾天平的耦合狀態和阻態個數也發生了明顯的變化.這就導致了該霍爾天平結構中HRR 值隨著NiO 厚度變化呈現非線性變化.例如, 當tNiO= 1 nm 時, 霍爾天平的Rp和Rap分別為2590 和3.7 mΩ, 其對應的HRR 比值達到69900%,這是目前報道的室溫下最高的霍爾電阻比值, 和沒有CoO 包覆的霍爾天平(圖7(f))結構相比較, HRR比值提高了302%.

為了闡明CoO 層調控霍爾天平HRR 比值的內在原因, 研究者們選取了HRR 比值為69900%的樣品進行微結構表征.圖9 給出了該樣品的低倍明場像透射電鏡照片和選區電子衍射照片[48], 其中圖9(a)中的低倍明場像透射電鏡照片表明了該霍爾天平結構的磁性多層膜具有良好的連續平整的層狀結構.選區電子衍射照片中的衍射環(如圖9(b)所示)表明, [Co/Pt]n多層膜為多晶結構.同時, 圖9(b)也顯示了NiO 和CoO 的(111)取向的電子衍射環.進一步對該樣品進行高分辨透射電鏡表征, 如圖10 所示[48].通過高分辨透射電鏡照片可以看出,霍爾天平材料整體呈現晶化狀態, 其中面間距0.242,0.22 和0.245 nm 分別對應于CoO(111), CoPt(111)和NiO(111)晶面, 說明了霍爾天平具有{111}CoO//{111}CoPt//{111}NiO//{111}CoPt//{111}CoO局部的外延生長關系.正是由于這種較好的晶體結構和局部外延關系的存在, 使得金屬/氧化物界面上的電子自旋相關散射得到增強, 因此通過界面調控在霍爾天平中實現了超高的HRR 比值.

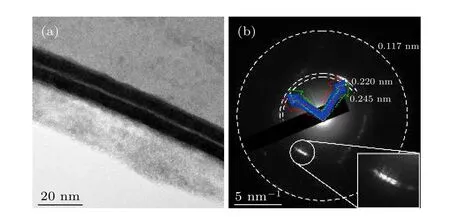
圖9 (a)樣品CoO(3)/[Pt(0.6)/Co(0.4)]4/Pt(0.3)/NiO(1)/[Co(0.4)/Pt(0.6)]4/CoO(3)(厚度單位均為納米)低倍透射電鏡照片; (b)上述樣品的選區電子衍射花樣照片[48]Fig.9.(a) Transmission electron microscope (TEM) image and (b) electron diffraction pattern for the sample CoO(3)/[Pt(0.6)/Co(0.4)]4/Pt(0.3)/NiO(1)/[Co(0.4)/Pt(0.6)]4/CoO(3)(in nm)[48].

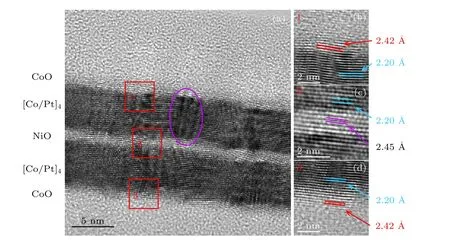
圖10 樣品CoO(3)/[Pt(0.6)/Co(0.4)]4/Pt(0.3)/NiO(1)/[Co(0.4)/Pt(0.6)]4/CoO(3)(厚度單位均為納米)高分辨透射電鏡照片[48]Fig.10.High resolution TEM image for the sample CoO(3)/[Pt(0.6)/Co(0.4)]4/Pt(0.3)/NiO(1)/[Co(0.4)/Pt(0.6)]4/CoO(3) (in nm)[48].

圖11 (a)?(d)樣品CoO/[Co/Pt]3/Co/Pt(tB)/NiO(1.1)/[Co/Pt]4/CoO(厚度單位為納米)的霍爾回線[49]Fig.11.(a)?(d) Hall loops for sample CoO/[Co/Pt]3/Co/Pt(tB)/NiO(1.1)/[Co/Pt]4/CoO (in nm)[49].

此外, 關于NiO 與[Co/Pt]n之間的界面氧遷移調控霍爾天平HRR 比值的相關研究也相繼展開.為了分別研究[Co/Pt]n/NiO 界面和NiO/[Co/Pt]n界面對霍爾天平HRR 比值的調控作用, 研究者設計并利用超高真空多靶磁控濺射鍍膜系統制備了兩組磁性多層膜樣品: S1: CoO/[Co/Pt]3/Co/Pt(tB)/NiO(1.1)/[Co/Pt]4/CoO;S2: CoO/[Co/Pt]4/NiO(1.1)/Pt(tT)/[Co/Pt]4/CoO(厚度單位為納米).圖11 是系列樣品S1 的霍爾輸出回線[49],可以看出, 當tB= 0 時, 霍爾天平呈現標準的鐵磁耦合狀態, 即二組態, 此時沒有HRR 比值.當tB=0.3 nm 時, 霍爾天平結構呈現明顯的反鐵磁耦合狀態, 即多組態, 此時霍爾天平的Rp和Rap分別為2480 和8 mΩ, 對應的HRR 比值達到30900%.繼續增加tB到0.6 nm 時, 霍爾天平保持了反鐵磁耦合狀態, 但Rp和Rap分別為2325 和139 mΩ,對應的HRR 比值降低到1570%.進一步增加tB到0.9 nm 時, 隨著中間狀態的消失, 霍爾天平的HRR 比值也隨之消失.圖12 是系列樣品S2 的霍爾輸出回線[49], 可以看出, 隨著tT的增加, 霍爾天平的HRR 比值呈現了非線性的變化規律.具體而言,tT= 0 時, 霍爾天平的HRR 比值達到1570% (Rp和Rap分別為2325 和139 mΩ); tT= 0.3 nm時,霍爾天平HRR 比值提高至18700% (Rp和Rap分別為2257 和12 mΩ); tT= 0.6 nm 時, 霍爾天平HRR 比值變化至5410% (Rp和Rap分別為2094和38 mΩ); tT= 0.9 nm 時, 霍爾天平沒有HRR比值.從上述結果不難看出的是, 隨著NiO 兩側Pt厚度的變化, 霍爾天平的阻態個數和HRR 比值得到顯著的調控, 這主要是由中間狀態和Rap變化所導致, 也說明界面處的Pt 層可以有效地調控霍爾天平的耦合狀態和HRR 比值.

為了進一步探索界面調控氧遷移對霍爾天平HRR 比值的調控機制, 可以利用X 射線光電子能譜(X-ray photoelectron spectroscopy, XPS)來精確探測界面原子狀態, 對上述兩個系列樣品S1 和S2 進行界面元素電子結構表征.關于XPS 表征技術原理及相關實驗細節, 可以參考之前的相關文獻[30,50].為更直觀地表征界面元素狀態、氧遷移行為等, 通常利用界面氧含量比率來標定.界面氧含量比率(ε)是根據XPS 能譜中元素各種價態的峰面積比值定義的, 計算公式為

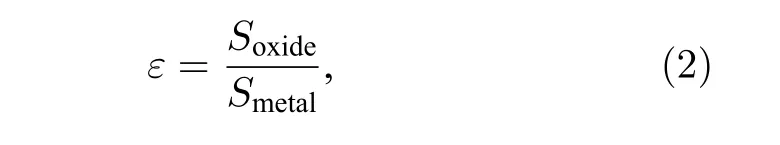
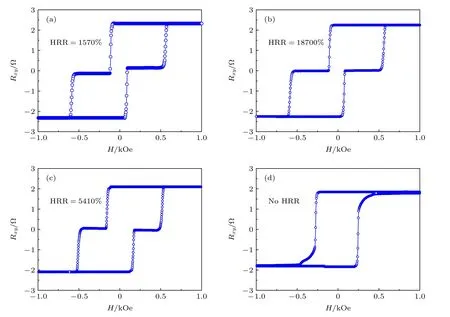
圖12 (a)?(d)樣品CoO/[Co/Pt]4/NiO(1.1)/Pt(tT)/[Co/Pt]4/CoO(厚度單位為納米)的霍爾回線[49]Fig.12.(a)?(d) Hall loops for the sample CoO/[Co/Pt]4/NiO(1.1)/Pt(tT)/[Co/Pt]4/CoO (in nm)[49].

其中Soxide和Smetal分別代表元素氧化態和金屬態XPS 峰面積值.圖13(a)和圖13(b)分別是霍爾天平中Co/NiO 界面和NiO/Co 界面的高分辨Co 2p3/2XPS 譜圖[49].當Co/NiO 界面沒有Pt 插層時, XPS 能譜中峰位位于777.8, 779.1 和781.3 eV,分別對應于Co0, Co2+和Co3+價態, 該結果說明在Co/NiO 界面處存在Co 的氧化物或者說Co—O鍵的形成.隨著Pt 插層厚度的不斷增加, Co 2p3/2的峰位并沒有發生改變, 但是峰面積比率發生了顯著的變化.當Pt 的厚度為0, 0.3, 0.6 和0.9 nm 時, ε值分別為1.7∶1, 2.2∶1, 2.9∶1 和1.5∶1, 如圖13(c)所示[49].與此同時, 界面Pt 插層的Pt 4f7/2XPS 峰位隨著Pt 層厚度的增加向著低結合能方向移動并始終高于塊材Pt 中的Pt 4f7/2XPS 峰位(70.8 eV),如圖13(d)所示[49].類似的情況也發生在NiO/Co界面上, 如圖13(b)所示[49].對于NiO/Co 界面而言, 無論是否有Pt 插層的引入, Co 2p3/2XPS 峰始終位于777.8, 779.1 和781.3 eV.當Pt 的厚度為0, 0.3, 0.6 和0.9 nm 時, ε 值 分 別 為3.3∶1,2.3∶1, 2.9∶1 和0.81∶1, 如圖13(c)所示[49].與之相對應的Pt 4f7/2峰也隨著Pt 厚度的增加而進一步向著低結合能移動, 如圖13(d)所示[49].根據上述結果可知, 界面超薄的Pt 插層可以有效地改變界面處的氧遷移狀態.這是因為Pt 插層的厚度都在亞納米量級, 與納米顆粒的性質相類似, 其表面具有較多的活性位點, 有利于界面處的電子軌道雜化和原子成鍵.例如, 在Co/NiO界面上引入厚度為0.3 nm 的Pt 層時, 非連續的Pt 具有十分高的活性能, 將促進Pt—O—Co 鍵的增加; 進一步增加Pt 層厚度至0.6 nm 時, 會導致Pt—O—Co 鍵的進一步增加; 當Pt 層厚度達到0.9 nm 時, Pt 層已經逐漸形成連續的層狀結構, 這時Pt 將會阻隔Co 和O 之間鍵合的形成, 從而導致Pt—O—Co鍵的顯著降低.界面上Pt—O—Co 鍵的多少反映了界面氧遷移的情況.需要特別說明的是, Co/NiO界面和NiO/Co 界面的調控作用還是有一些不同的, 這主要是鐵磁層和氧化物層的生長順序不同所導致的.從霍爾天平HRR 值的調控結果來看, 只有當Pt 層為0.3 nm時, 其HRR 比值為極大值.此時, 其界面處的氧含量比率約為2.3∶1, 這就說明了只有適度氧遷移下界面Pt—O—Co 鍵形成時才有利于超高HRR 比值的獲取.過度氧化或者欠氧化的狀態(氧含量比率過高或者過低)都會導致霍爾天平中的HRR 比值顯著降低.

4 霍爾天平中的磁性斯格明子多場調控

過去一段時間, 科學家們利用磁性多層膜中的均一化磁化狀態作為信息存儲的基礎進行新材料、新結構和新原理型器件的設計開發.近些年來, 非共線的自旋結構(局域磁化狀態)由于具有拓撲保護等諸多物理特性而逐步得到了人們廣泛的關注.磁性斯格明子是一種具有拓撲保護特性非共線手性自旋結構, 由材料體系中多種能量相互競爭所導致, 具有豐富的物理內涵[51].特別是, 磁性斯格明子的尺寸通常為納米尺度, 且具有較低的臨界翻轉驅動電流密度(約 102A/cm2)遠低于當前磁性隧道結的臨界翻轉電流密度[19], 這一系列的物理特性使其在磁性隨機存儲器件設計中展現了巨大的潛在應用前景.因此, 磁性材料中磁性斯格明子的多場調控及相關原理型器件研究是近年來自旋電子學領域的研究熱點之一.

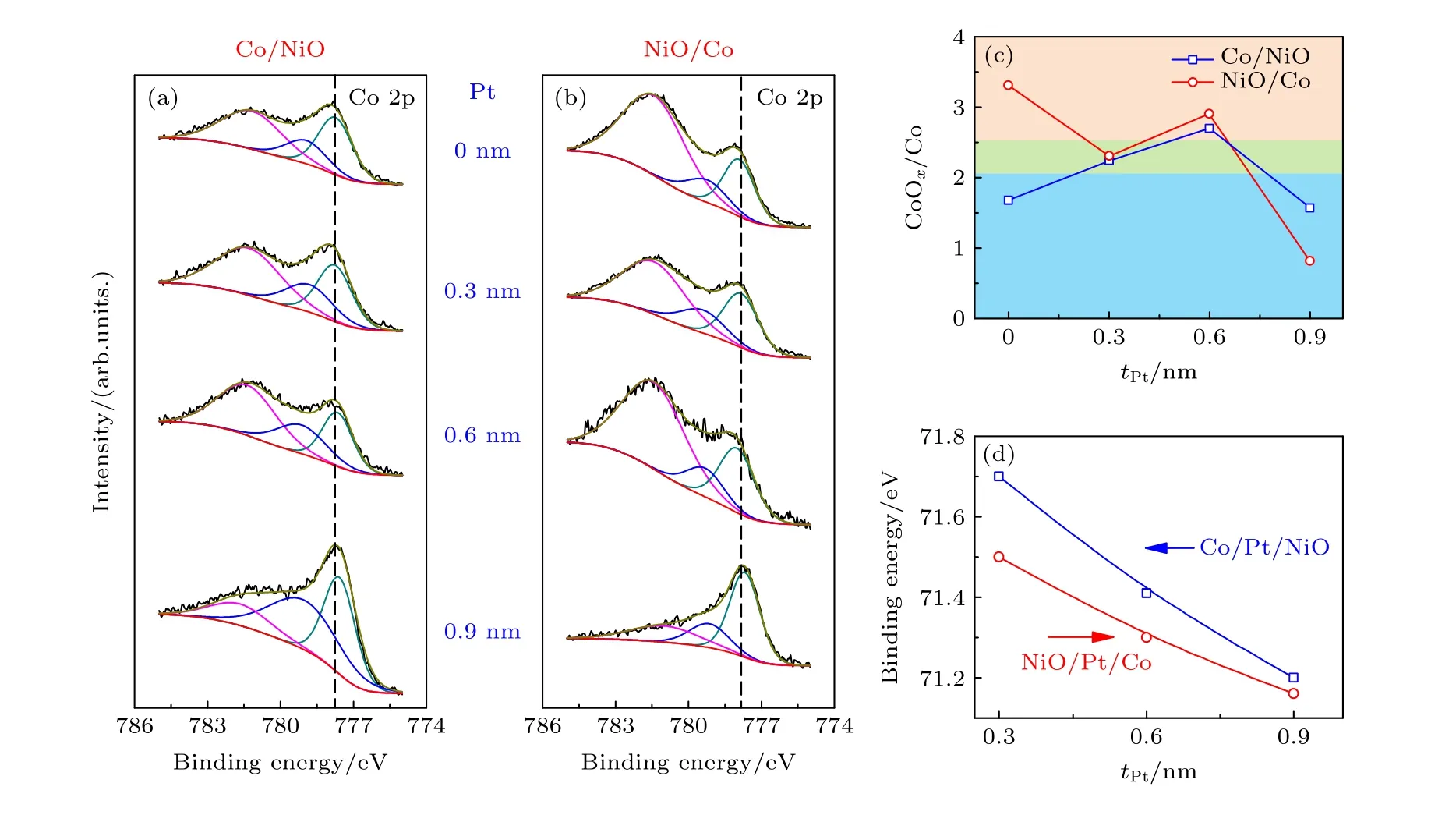
圖13 (a), (b)Co/NiO 界面和NiO/Co 界面上高分辨Co 2p XPS 圖譜; (c)界面CoOx/Co 比率隨Pt 厚度變化規律; (d)界面Pt 4f 結合能隨界面Pt 厚度變化規律[49]Fig.13.(a), (b) High resolution XPS Co 2p spectra at Co/NiO interface and NiO/Co interface; (c) interfacial CoOx/Co content and(d) Pt 4f binding energy as a function of the Pt thickness at interfaces[49].

近期的研究結果顯示最近鄰交換作用、Dzyaloshinskii-Moriya interaction(DMI)作用、磁偶極能和磁各向異性對磁性斯格明子的形成具有重要影響[52].其中, 磁性材料中由空間對稱性破缺引入的手性相互作用(例如DMI 作用)促使自旋傾向于非平行排列, 是形成非共線自旋結構的重要起因之一.通常情況下, 磁性斯格明子分為兩大類: 布洛赫型磁性斯格明子和奈爾型磁性斯格明子.關于磁性斯格明子的研究也逐漸從二元合金、復雜氧化物單晶擴展到多元合金、磁性納米復合結構、磁性多層膜體系等, 從低于室溫向室溫發展.多元、復合納米結構使得磁性斯格明子中不同的物理機理相互競爭, 其形成和動力學過程也受到了納米薄膜材料本身結構、組分、界面等一系列因素的影響[53?59],而針對上述內容, 科學家們相繼開展了一系列的研究工作[60?63].目前, 觀察磁性斯格明子的技術手段主要包括洛倫茲透射電鏡(Lorentz TEM, L-TEM)、自旋極化掃描隧道顯微鏡(SP-STM)、磁力顯微鏡(MFM)、磁光克爾顯微鏡(MOKE)和光發射電子顯微鏡(PEEM)等.其中, L-TEM 技術的發展為磁性斯格明子的實空間表征提供了快速和有效的實驗平臺.例如, Yu 等[64]利用L-TEM 首次在Fe0.5Co0.5Si 單晶體系中觀察到二維磁性斯格明子拓撲自旋結構, 為磁性斯格明子的實空間觀察提供了一條有效途徑.隨后, 磁性斯格明子相繼在FeGe[65], Cu2OSeO3[66]等多個體系中被觀察到.對于磁性斯格明子新物態的調控也逐步得到人們的重視[67?69].與此同時, 國內外的專家學者們將目光轉向磁性薄膜中的斯格明子探索, 并在理論和實驗上取得了許多可喜的研究成果[70?74].大量的研究使得人們對于鐵磁材料中的磁性斯格明子觀察和調控有了一定程度的認識, 但是利用磁性斯格明子薄膜材料設計新型的磁信息存儲器件的研究仍有大量工作需要開展.關于磁性斯格明子的研究進展可以參考相關綜述文章[75?80].

隨著磁性斯格明子相關研究的逐步開展, 人們在理論和實驗上均發現鐵磁多層膜中的斯格明子在外部激勵(電流或者電壓)下沿著電流方向運動的同時, 還會向橫向漂移并在側向發生積累和湮滅.這一物理現象和大家熟知的霍爾效應相類似,因此被命名為斯格明子霍爾效應(Skyrmion Hall effect, SkHE)[81].由于SkHE 的存在, 磁性斯格明子作為存儲單元的賽道存儲器件無法有效地進行信息存儲和傳遞, 這使得肩負著未來希望的基于斯格明子賽道存儲器件的進一步實用化蒙上了一層陰影.

為了突破當前鐵磁薄膜中磁性斯格明子所面臨的困境, 人們也在不斷尋找能夠降低或者完全消除SkHE 的新材料.隨著研究的不斷深入, 具有兩套自旋晶格的亞鐵磁和反鐵磁材料逐步得到了人們的關注.2017 年, Zhang 等[82]利用微磁學模擬研究了人工反鐵磁體中斯格明子的動力學過程, 模擬結果顯示上下兩鐵磁層中出現一對磁性斯格明子, 且它們受到大小相等、方向相反的馬格努斯力,可以實現電流驅動下的直線運動.2018 年, Akosa等[83]從理論上提出了反鐵磁體中的斯格明子在電流驅動下可以完全消除SkHE, 這主要是由于反鐵磁體中兩套完全相反的自旋晶格受到的馬格努斯力完全抵消所導致的.隨后不久, 一些相關的理論工作也相繼被報道[84,85], 這些研究成果為科學家們在實驗上尋找新的斯格明子材料指明了一條極具希望之路.但是, 相關實驗工作并不順利, 探索道路十分坎坷.

眾所周知, 反鐵磁體中的兩套自旋結構在嚴格意義上是成反平行排列的, 宏觀凈磁矩為零, 這就導致反鐵磁體的自旋結構觀察和探測極具挑戰性,這也是當前自旋電子學領域的一大難題.而亞鐵磁體中兩套自旋晶格部分補償抵消, 宏觀上具有較弱的凈磁矩, 這就為自旋狀態和磁疇結構的觀察提供了可能.隨后, 一系列的理論和實驗研究成果顯示SkHE 在亞鐵磁多層膜材料中可以被有效地抑制,同時斯格明子的動力學過程也可以得到調制[86,87].但是, 如何在反鐵磁體中實現斯格明子的觀察和多場調控仍然是人們普遍關注的熱點問題之一.

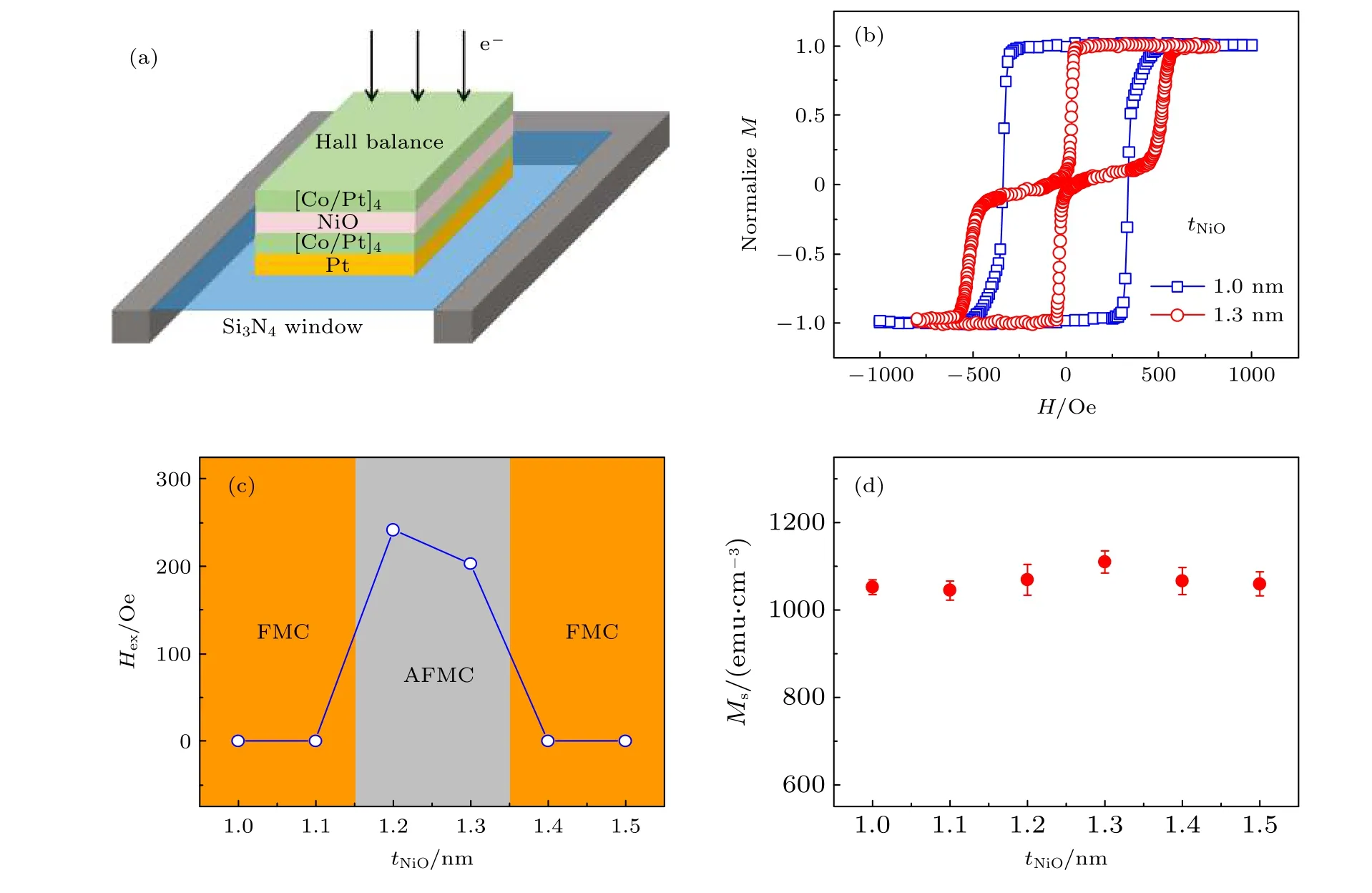
圖14 (a)霍爾天平的結構示意圖; (b)具有鐵磁耦合和反鐵磁耦合霍爾天平的垂直膜面方向的磁滯回線; (c)霍爾天平的交換耦合場和(d)飽和磁化強度隨NiO 厚度變化規律[88]Fig.14.(a) Schematic of Hall balance in L-TEM measurement; (b) normalized M-H loops for the sample with ferromagnetic coupling and antiferromagnetic coupling, respectively; (c) shifted field and (d) saturation magnetization as a function of NiO thickness[88].

鑒于目前磁性斯格明子研究所遇到的挑戰, 我國科學家利用洛倫茲透射電鏡技術在具有反鐵磁耦合的霍爾天平結構中首次發現了高密度的磁性斯格明子并實現了對磁性斯格明子的多場調控.圖14(a)給出了霍爾天平的結構示意圖[88].這里選擇的霍爾天平與前文所述的在結構上稍微有所不同, 主要是Pt 底層為后續調控霍爾天平的磁疇狀態提供了自旋流.圖14(b)給出了兩種典型的具有鐵磁耦合(tNiO= 1 nm)和反鐵磁耦合(tNiO=1.3 nm)霍爾天平結構的磁滯回線[88].從磁滯回線可以看出, 霍爾天平結構中的反鐵磁耦合狀態下剩余磁矩接近于0, 主要是因為霍爾天平中兩個鐵磁層的磁矩反平行排列且大小幾乎相等.圖14(c)給出了霍爾天平結構中交換耦合場隨隔離層NiO 厚度的變化規律曲線.隨著NiO 厚度的增加, 霍爾天平的耦合狀態在鐵磁耦合和反鐵磁耦合間呈現振蕩變化規律.但是, 霍爾天平的飽和磁化強度并不隨著NiO 厚度的改變而變化, 如圖14(d)所示.

圖15(a)和圖15(b)分別是鐵磁耦合和反鐵磁耦合狀態下霍爾天平結構在基態時的洛倫茲透射電鏡照片[88].這里的基態是指對霍爾天平材料施加垂直于膜面磁場至正向飽和后再撤掉磁場的狀態.洛倫茲透射電鏡照片表明: 基態下霍爾天平結構無論是在鐵磁耦合或反鐵磁耦合狀態下, 視野中基本上看不到明顯的磁疇結構.在此基礎上, 對霍爾天平施加外部激勵(垂直磁場和面內脈沖電流),然后撤掉外部激勵, 再利用洛倫茲透射電鏡對霍爾天平進行觀察, 如圖15(c)和圖15(d)所示[88].可以看出, 具有鐵磁耦合和反鐵磁耦合的霍爾天平結構中均發現了高密度的磁性斯格明子, 其密度約為7.5 μm–2.

圖15 (a), (b)鐵磁耦合和反鐵磁耦合霍爾天平基態下的洛倫茲透射電鏡照片; (c), (d)鐵磁耦合和反鐵磁耦合霍爾天平激勵后的洛倫茲透射電鏡照片[88]Fig.15.L-TEM images for Hall balance at ground state with (a) ferromagnetic coupling and (b) antiferromagnetic coupling, respectively.High density of skyrmions in a Hall balance after drawing excitation with (c) ferromagnetic coupling and (d) antiferromagnetic coupling, respectively[88].

隨后, 研究者們利用洛倫茲透射電鏡的樣品與電子束角度可調功能進一步研究霍爾天平中磁性斯格明子的性質.圖16(a)—圖16(c)分別是不同角度下的霍爾天平中的斯格明子磁結構[88].當角度為0°時, 無法觀察到磁性斯格明子; 當角度為±15°時, 霍爾天平中的磁性斯格明子的黑白襯度發生翻轉, 這一研究結果也說明了霍爾天平中的磁性斯格明子為奈爾型斯格明子.研究人員選取其中一個斯格明子在角度為 ± 15°下的圖像, 進行了斯格明子尺寸的標定, 顯示霍爾天平中的磁性斯格明子大小為180 nm 左右.綜上所述, 室溫下霍爾天平結構可以形成零場下的高密度奈爾型磁性斯格明子, 這為后續基于霍爾天平磁性斯格明子的存儲器件提供了材料基礎.

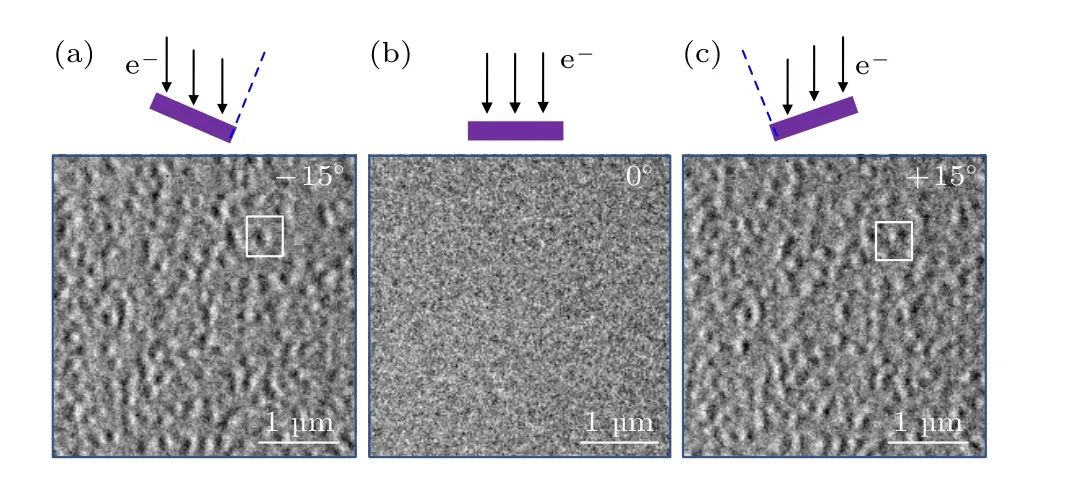
圖16 (a), (b)和(c)分別是不同角度下的霍爾天平中的磁性斯格明子[88]Fig.16.(a), (b), (c) Magnetic skyrmions in a Hall balance with various tilting angle[88].

為了進一步闡明霍爾天平中磁性斯格明子形成和調控機制, 對霍爾天平磁結構進行精確表征就顯得尤為重要.幸運的是中國散裂中子源(CSNS)在近期投入運行, 它是國家“十一五”期間重點建設的國家大科學裝置, 是發展中國家擁有的第一臺散裂中子源, 是國際前沿的高科技多學科應用的大型研究平臺, 與正在運行的美國、日本和英國散裂中子源一起構成世界四大散裂中子源.該實驗平臺為我國在物理學、化學、生命科學、材料科學、納米科學、醫藥、國防科研和新型核能開發等學科前沿領域的研究提供了一個先進、功能強大的科研平臺.特別指出的是, 中子散射技術在確定磁性材料的原子結構和磁結構方面具有得天獨厚的優勢, 可以為材料結構優化和物理機理研究提供強有力的微結構表征技術支持.

針對磁性多層膜樣品而言, 國內科學家們相互合作, 利用極化中子反射技術(polarized neutron reflectometry, PNR)對面內磁矩的高敏感特性,從而定量分析磁性多層膜中的磁矩分布情況.當具有不同極化方向的中子束流入射到磁性多層膜樣品表面時, 通過收集測量不同極化方向的反射中子束流強度隨動量轉移矢量Q 的變化關系, 可獲得磁性多層膜中磁性深度分布信息.通常情況下, PNR技術具有無損穿透的特性的同時, 還可實現超高的空間分辨率和極低的磁性探測.因此, PNR 技術在磁性多層膜中磁結構深度分布的精準測量具有獨特的技術優勢, 為研究非共線磁結構等復雜自旋結構提供了有效途徑.PNR 技術的應用已在解決自旋電子學領域熱點問題中發揮了重要作用.關于中子散射技術在磁性材料中的應用可以參考朱濤研究員撰寫的綜述及相關文章, 這里不再贅述[89?91].

圖17(a)和圖17(b)分別是低場下和高場下具有反鐵磁耦合霍爾天平的極化中子反射譜圖[88].當施加外磁場(9000 Oe, 如圖17(b)所示)遠大于霍爾天平飽和場時, 薄膜樣品的磁矩均在面內方向, 不同極化方向的中子反射曲線呈現明顯的差別;當施加外磁場接近零(20 Oe, 如圖17(a)所示)時,薄膜樣品的磁矩基本為剩余磁化狀態, 不同極化方向的中子反射曲線基本重合.通過對自旋不對稱(spin asymmetry, SA)曲線的擬合, 研究者們發現低場下具有反鐵磁耦合的霍爾天平呈現了一個非常小的面內磁矩分量.根據擬合結果可知, 具有反鐵磁耦合的霍爾天平具有傾斜的界面磁結構, 靠近NiO 隔離層的Co 層呈現7°的傾斜角, 如圖17(c)所示[88].根據相同的方法, 研究者們發現具有鐵磁耦合的霍爾天平也具有4°的傾斜角, 中子結果和磁結構解析如圖17(d)—圖17(f)所示.界面傾斜磁矩的實驗驗證有助于人們更加深入地理解霍爾天平結構中斯格明子的形成機制, 同時為多場調控霍爾天平中的磁性斯格明子提供了一條思路.

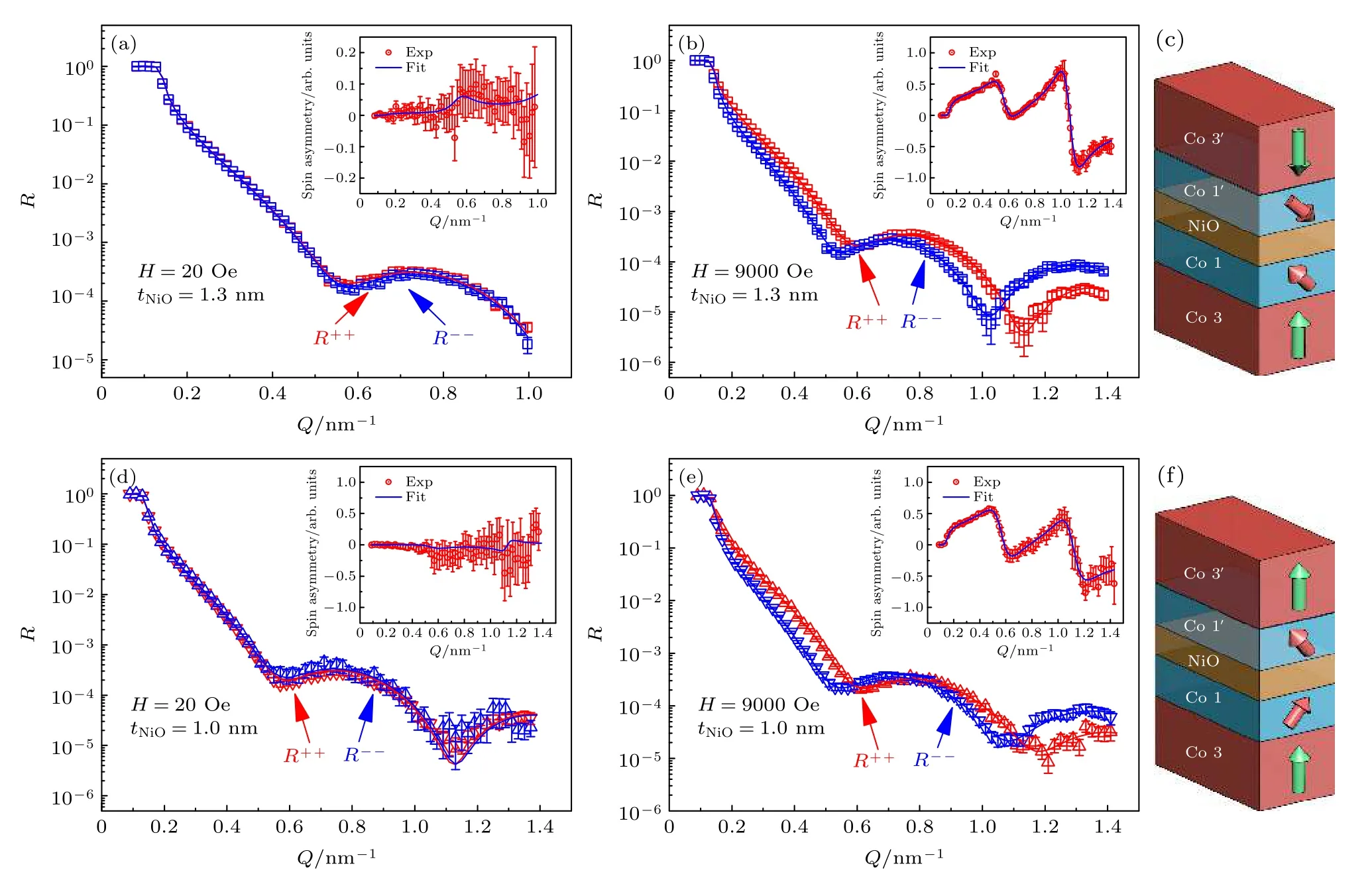
圖17 (a)和(b)分別是低場下和高場下具有反鐵磁耦合霍爾天平的極化中子反射譜圖; (c)具有反鐵磁耦合的霍爾天平自旋結構示意圖; (d)和(e)分別是低場下和高場下具有鐵磁耦合霍爾天平的極化中子反射譜圖; (f)具有鐵磁耦合的霍爾天平自旋結構示意圖[88]Fig.17.PNR spectra as a function of Q measured with in-plane (a) low and (b) high magnetic fields for the Hall balance with antiferromagnetic coupling; (c) schematic of the magnetic structure of the Hall balance with antiferromagnetic coupling; PNR spectra as a function of Q measured with in-plane (d) low and (e) high magnetic fields for the Hall balance with ferromagnetic coupling;(f) schematic of the magnetic structure of the Hall balance with ferromagnetic coupling[88].

微磁學模擬有助于加深對霍爾天平中磁性斯格明子形成與調控機制的理解, 相關的研究工作圍繞霍爾天平中的耦合強度(EIEC)和易磁化軸方向(θ)與磁性斯格明子之間的內在關系展開.首先,研究者設定易磁化軸為90°, 同時改變耦合強度.圖18(a)是基態下具有不同反鐵磁耦合強度的霍爾天平中的磁性斯格明子[88].因為霍爾天平中的磁性斯格明子是成對出現的, 這里只給出了下層[Co/Pt]n多層膜中的磁結構信息.當EIEC<–1.4 mJ/m2時, 霍爾天平結構無法形成穩定的磁性斯格明子; 當EIEC= –1.5 mJ/m2時, 霍爾天平中的磁性斯格明子密度達到100 μm–2; 繼續增加EIEC至–2.4 mJ/m2時, 磁性斯格明子的密度顯著降低.圖18(b)給出了霍爾天平中磁性斯格明子密度隨EIEC和θ 變化的相圖[88].從相圖可知, 只有當反鐵磁耦合強度達到一定值時, 霍爾天平中才會形成穩定的磁性斯格明子.同時, 對不同的易磁化軸角度θ 而言, 形成磁性斯格明子的耦合強度閾值呈現明顯的變化.當反鐵磁耦合強度在–1.5 mJ/m2附近時, 磁性斯格明子密度達到極大值.即使在反鐵磁耦合強度較大的情況下, 霍爾天平中的磁性斯格明子的密度仍然可以保持較高的水平(25 μm–2).圖18(c)和圖18(d)是在霍爾天平基態的基礎上施加外部激勵并撤除后不同耦合強度下的霍爾天平中磁結構信息[88].不難看出的是, 外部激勵施加過后霍爾天平中的斯格明子的個數明顯增加.即使在耦合強度很低的情況下, 霍爾天平中仍然存在著數目相當的磁性斯格明子.這也說明了外部激勵促使出現磁性斯格明子對應的耦合強度能量范圍變寬了.外部激勵的施加對霍爾天平中磁疇結構產生了顯著的影響, 并且脈沖電流在Pt 底層中產生了自旋流注入到霍爾天平核心結構中, 上下兩層[Co/Pt]n多層膜受到自旋流影響并不相同, 從而導致了上下鐵磁層中不同的磁疇結構.上述微磁學模擬結合實驗結果可以讓人們更好地理解霍爾天平中的拓撲磁性及調控機制, 為后續的原理型器件的設計打下堅實的基礎.

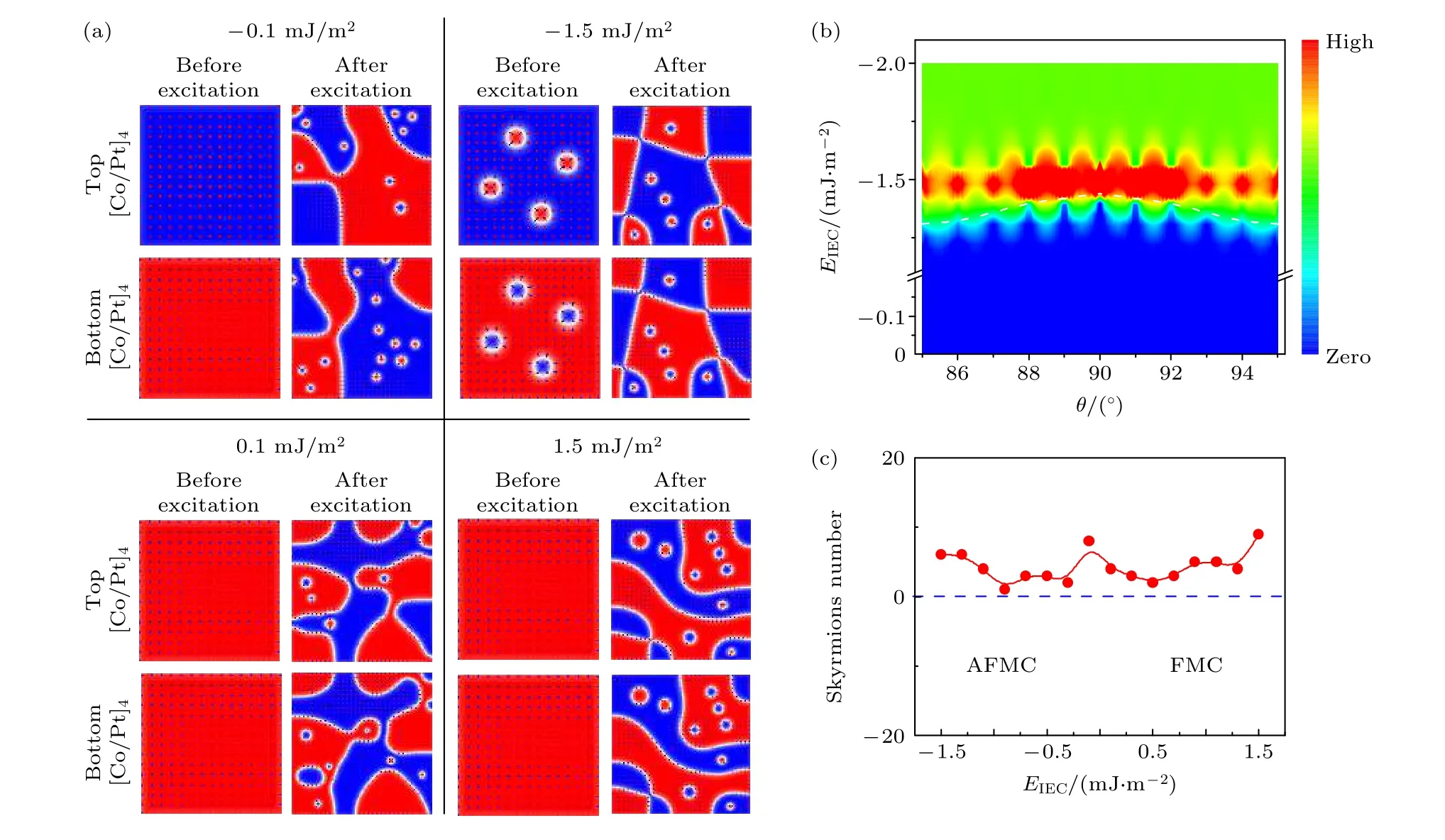
圖18 (a)具有不同層間耦合強度的霍爾天平中的基態和激勵后的磁性斯格明子; (b)基態下霍爾天平中磁性斯格明子密度隨EIEC 和θ 變化的相圖; (c)外部激勵撤除后霍爾天平中磁性斯格明子個數隨層間耦合強度的變化規律曲線[88]Fig.18.(a) Simulated skyrmions in a Hall balance with various EIEC; (b) contour map of the skyrmion density as a function of EIEC and θ without external excitation; (c) the skyrmion number as a function of EIEC in Hall balance with drawing excitation[88].

與此同時, 研究者們也開展了電流驅動霍爾天平中斯格明子運動的動力學研究.鑒于該結構的霍爾天平中磁性斯格明子尺寸較小以及較強的釘扎作用, 利用電流驅動斯格明子的實驗十分具有挑戰性.為了更好地理解霍爾天平中磁性斯格明子的動力學過程, 研究者利用微磁學模擬的方法對其進行了系統研究.結果發現, 具有鐵磁耦合的霍爾天平中磁性斯格明子在電流驅動作用下向前運動的同時發生顯著偏轉.然而, 具有反鐵磁耦合霍爾天平中的磁性斯格明子會在電流驅動作用下沿著直線向前運動, 展現了較強的器件實用性.因此, 對于霍爾天平中磁性斯格明子動力學的相關實驗仍然在進行中.

5 霍爾天平在其他材料體系中的擴展與應用

隨著霍爾天平材料及相關器件設計的研究不斷深入, 基于霍爾天平的高密度存儲邏輯器件逐步受到了人們的普遍關注[92?98].基于霍爾天平材料的概念, 人們也將這一理念推廣到其他材料體系中, 并且獲得了一系列可喜的研究進展.

荷蘭代爾夫特理工大學Caviglia 團隊[97]利用脈沖激光沉積技術制備了一種全氧化物的霍爾天平材料, 其核心結構為SrRuO3/SrTiO3/SrRuO3(SRO/STO/SRO)三明治結構.該團隊利用原子級厚度控制可以實現霍爾天平中兩個磁性層的霍爾輸出信號的調控, 進而實現霍爾天平多組態的功能化.與此同時, 研究還發現SRO/STO/SRO 霍爾天平中的反常霍爾效應具有很強的溫度依賴特性.圖19 給出了不同溫度下SRO/STO/SRO 霍爾天平的反常霍爾輸出曲線, 并對霍爾天平中雙鐵磁層的反常霍爾信號進行解析[97].研究結果表明,隨著測試溫度的不斷提高, 霍爾天平的反常霍爾信號在特定溫度區間發生符號翻轉, 這主要是由STO層反常霍爾效應的內稟貢獻與相轉變溫度息息相關所導致的.對于具有不同厚度的STO 層的磁相變溫度并不相同.因此, 利用對不同厚度的STO層的溫度調控可以實現其反常霍爾效應的調控, 從而實現霍爾天平多組態功能.

近期, 德國科隆大學的Vrejoiu 研究團隊[98]利用脈沖激光沉積技術制備了霍爾天平SrRuO3/SrIrO3/SrRuO3(SRO/SIO/SRO)多層膜, 并利用磁電輸運性質測試對該材料體系中拓撲霍爾效應和反常霍爾效應進行深入研究并探討異常的霍爾回線形成機理, 澄清了拓撲霍爾效應與磁性斯格明子探測之間的內在關系.雖然近期的多數工作都是利用磁性多層膜中的拓撲霍爾效應來表征并探測磁性斯格明子的形成[99,100], 但該研究結果表明霍爾天平SRO/SIO/SRO 中反常霍爾輸出曲線是鐵磁層反常霍爾電壓符號的不同所導致的.該材料體系中的反常霍爾效應與磁性層厚度、溫度和界面化學勢等諸多因素相關.因此, 該研究結果表明不能只利用反常霍爾回線來探測并表征磁性斯格明子的存在.

6 結論與展望

鑒于豐富的物理內涵以及在信息磁存儲器件設計中巨大的潛在應用前景, 霍爾天平自提出之后就受到了人們的廣泛關注.以霍爾天平結構為核心的磁存儲原理型器件的提出, 突破了傳統二組態信息存儲模式, 實現了信息多組態磁存儲的同時, 也可以完成多種布爾邏輯運算.這種新型的存算一體化器件構架設計, 解決了當前基于GMR, TMR 的傳統二組態自旋電子學材料器件的技術瓶頸, 其超高霍爾電阻比值突破了當前磁電阻與半導體電阻開關比相差甚遠的窘境.霍爾天平提出之初, 人們普遍認為具有垂直磁各向異性的霍爾天平的磁矩應該垂直于薄膜平面.國內學者利用中國散裂中子源這一大科學裝置優勢平臺獲得了突破性進展, 首次證實了垂直霍爾天平材料中具有角度可控的傾斜磁矩, 這也為霍爾天平中拓撲磁性相關研究的開展提供了強有力的實驗依據.基于這一重要研究結果, 利用洛倫茲透射電鏡技術結合多場調控手段在霍爾天平材料中成功觀察到高密度室溫奈爾型磁性斯格明子.從實驗和微磁學模擬兩個角度深入研究發現, 霍爾天平的層間耦合作用和界面磁矩傾斜程度都極大地影響著磁性斯格明子的形成, 為下一步設計基于磁性斯格明子的霍爾天平原理型器件提供了有力的理論和實驗依據.此外, 還利用微磁學模擬的方法揭示了霍爾天平中磁性斯格明子的動力學過程, 研究結果顯示, 具有反鐵磁耦合的霍爾天平中磁性斯格明子在電流驅動過程中斯格明子霍爾效應可以被完全抑制, 磁性斯格明子可以在電流驅動下沿直線運動, 這對設計基于斯格明子的賽道存儲器件有著重要的指導意義.這些研究成果為推動新型自旋電子學材料的研究開辟了一條新的研究思路.目前, 利用原位多場調控技術在霍爾天平材料中可以實現磁性斯格明子的產生、湮滅和密度調制等多種狀態轉換.但是, 利用電流驅動霍爾天平中磁性斯格明子運動的實驗工作卻遇到了一些困難.這主要是因為磁性多層膜中較大的釘扎作用導致了驅動電流密度居高不下, 同時霍爾天平材料中磁性斯格明子尺寸較小, 克服釘扎勢壘進行運動所需要的能量較高.因此, 霍爾天平材料中磁性斯格明子動力學的相關實驗研究將是下一步關注的一個十分重要的問題.針對這一問題, 后續的工作將重點通過優化磁性多層膜的生長質量降低缺陷等釘扎位點, 尋找合適的磁性層和功能層, 從材料、物理和器件設計多角度綜合考慮, 力圖深入研究多場調制下磁性斯格明子動力學過程.

與此同時, 霍爾天平的概念已經擴展到氧化物多層膜結構、二維范德華異質結等低維結構中.但是, 如何實現基于霍爾天平結構的磁存儲邏輯計算一體化器件的全電場調控, 如何設計基于霍爾天平結構的磁性斯格明子賽道存儲器件, 如何深入理解霍爾天平中拓撲磁性調控的物理機理, 如何解決當前霍爾天平材料與半導體工藝器件的兼容等一系列科學問題的解決仍然面臨挑戰.這些問題的澄清需要更加深入的理論分析與實驗驗證相結合.隨著國內外對霍爾天平材料及原理型器件關注度逐步升溫, 結合先進的技術手段和大科學裝置的投入使用, 基于霍爾天平的信息磁存儲器件及多場調控物理機理的相關研究將會取得更多突破性研究成果.

感謝中國科學院物理研究所蔡建旺研究員、孫陽研究員、張穎研究員、于國強研究員在磁性材料表征方面予以的幫助與指導; 感謝中國科學院半導體所王開友研究員在自旋輸運表征方面予以的幫助與指導; 感謝中國散裂中子源朱濤研究員在極化中子反射譜儀表征方面予以的幫助與指導; 感謝四川師范大學趙國平教授在微磁學模擬理論方面予以的幫助與指導.