新型大行程高承載力的柔性鉸鏈設計

趙傳森， 許 勇， 張強強， 王 艷， 董 飛

(上海工程技術大學 機械與汽車工程學院， 上海 201620)

隨著柔性機構的飛速發展，具有尺寸緊湊、輕量化、無摩擦、無潤滑和無磨損等優點的柔性鉸鏈和柔性機構已經在汽車工業、電子工業、微操作機器人及精密光學儀器等領域得到廣泛應用[1-5]。

對于柔性鉸鏈的研究已經有了大量的文獻參考[6-7]。JACOBSEN等[8]提出了平板折展扭轉柔性鉸鏈(LET)，推導了鉸鏈的扭轉等效剛度和拉壓等效剛度，并進行了有限元驗證，表明LET鉸鏈適用于需要大角度旋轉但離軸剛度不高的應用范疇。李宗軒等[9]提出了一種Cartwheel 型雙軸柔性鉸鏈，該鉸鏈結構是由帶圓角的短直梁復合而成，利用有限元分析的方法對其剛度和應力性能指標進行了分析驗證，確定了其幾何尺寸。陳貴敏等[10]提出了一類深切口橢圓柔性鉸鏈，運用材料力學理論推導了轉角、精度和最大應力解析公式，運用Ansys有限元仿真軟件驗證了公式的正確性。宗光華等[11]發明了一種雙曲桿型空心柔性鉸鏈，該鉸鏈中間是空心設計，用簧片式代替傳統的切口型柔性鉸鏈，提高了轉動范圍并降低了內應力，適用于大行程的工程應用。文獻[12-13]發明了一種交叉簧片轉動型柔性鉸鏈，通過多簧片在空間交叉但并不在交叉點處固定的設計，使得鉸鏈的變形更大，精度較高。GOLDFARB等[14]提出了一種具有獨特旋轉彎曲的裂桶型柔性鉸鏈，通過提供更好的多軸旋轉特性，對比傳統的薄梁彎曲鉸鏈，該鉸鏈能夠實現更大的運動范圍。

這些柔性鉸鏈雖然都有自己的優勢表現，但很難同時滿足行程、承載能力及失效等性能指標要求，多數柔性鉸鏈存在軸漂大、承載力小、塑性變形及穩定性差等問題。為了解決這些問題，很多學者將研究集中到開發新型柔性鉸鏈中。有鑒于此，課題組也力求從這些角度進行突破，提出了一種新型TLET柔性鉸鏈。該鉸鏈具有行程大，承載能力大，工作環境安全可靠等特點，在現代機構發展階段中具有潛在的應用前景。

課題組設計了一種具有大行程、高承載力的新型柔性鉸鏈(TLET)。將LET柔性鉸鏈以串并聯的方式布置，建立了等效剛度模型。對不同材料的柔性鉸鏈進行了失效分析，通過有限元仿真驗證了鉸鏈的可行性。最后將新型TLET柔性鉸鏈和傳統LET柔性鉸鏈進行了比較。

1 新型柔性鉸鏈設計

為了使柔性鉸鏈受力時產生較大的位移范圍，課題組提出一種新型LET陣列，命名為TLET鉸鏈，如圖1所示。傳統設計方案，一般只設計為2個分支，但有些特殊需求，需要增加分支的數量。一組耦合的LET分支被改變時，位移和剛度都會發生改變。在本文中，我們選擇2個耦合的LET鉸鏈來研究整個柔性鉸鏈的性能。基于LET鉸鏈陣列，所提出的柔性鉸鏈在x軸方向有較大位移，載荷范圍較大，同時z軸方向也有較大位移。LET鉸鏈分別由扭桿1、扭桿2和彎桿1、彎桿2組成。利用串并聯布置方式的特性，可以增大沿x軸和z軸方向上的位移。

圖1 TLET柔性鉸鏈三維模型Figure 1 3D model of TLET flexure hinge

圖2為新型柔性鉸鏈的二維幾何尺寸圖。TLET鉸鏈在水平方向和豎直方向上對稱分布，包括厚度t、寬度w、長度l以及扭桿和彎桿的幾何參數。扭桿1和扭桿2的長度分別為lT1和lT2，寬度分別為wT1和wT2;彎桿1和彎桿2的長度分別為lB1和lB2，寬度分別為wB1和wB2。表1給出了鉸鏈的主要幾何參數的詳細說明。

圖2 TLET柔性鉸鏈的二維幾何尺寸Figure 2 Two-dimensional geometry of a TLET flexure hinge

表1 柔性鉸鏈設計參數的詳細說明Table 1 Detailed description of flexure hinge design parameters mm

邊界條件如下：沿x軸在A點施加壓縮荷載F，產生x軸方向壓縮位移和平面外z軸方向的位移。

2 等效剛度模型的建立

為了分析TLET柔性鉸鏈的剛度性能，我們確定了彈簧常數的等效方程。把每個節段都假設為彈簧，同時每個彎桿和扭桿都簡化為彎曲和扭轉彈簧，如圖3所示。TLET鉸鏈的整體剛度可分為彈簧系統Ⅰ、Ⅱ，其中彎桿2連接這2個系統，分別將kT1，kB1和kT2串聯再并聯，形成一個整體系統，標記為彈簧系統Ⅰ；同理，可得到彈簧系統Ⅱ。

考慮到系統Ⅰ的上部，包括3個串聯的kT1，kB1和kT2，其等效剛度為

式中：keq,topⅠ，kT1，kB1和kT2分別表示彈簧系統Ⅰ上部的等效剛度，扭桿1的剛度，彎桿1和扭桿2的剛度。

系統Ⅰ的下部與上部相同，因此彈簧系統Ⅰ的總等效剛度為

式中KeqⅠ表示彈簧系統Ⅰ的總等效剛度。

由于柔性鉸鏈對稱布置，彈簧系統Ⅱ的總等效剛度等于彈簧系統Ⅰ的總等效剛度，即

式中KeqⅡ表示彈簧系統Ⅱ的總等效剛度。

如圖3所示，所有彈簧都是串并聯的。基于此假設，TLET型柔性鉸鏈的總等效彈簧常數Keq，TLET為

其中彎桿1和彎桿2的剛度計算公式為：

式中E是彈性模量。

扭桿1和扭桿2的剛度計算公式為：

式中：G是剛性模量，ν是泊松比。

沿x軸輸入載荷與TLET柔性鉸鏈輸出位移之間的關系為

式中：F為載荷，δ為柔性鉸鏈沿x軸的位移。

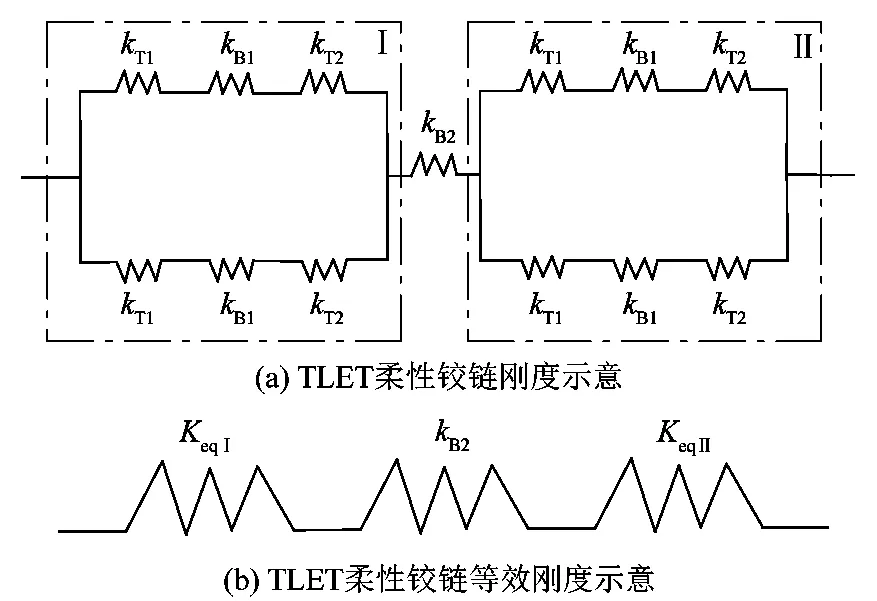
圖3 TLET柔性鉸鏈等效彈簧模型Figure 3 Equivalent spring model of TLET flexure hinge

3 失效分析

在柔性鉸鏈工作過程中，會出現蠕變、屈曲、塑性變形和疲勞斷裂等失效形式，其中塑性變形破壞和屈曲現象是柔性鉸鏈最需要解決的兩種失效形式。提出的柔性鉸鏈需在材料的彈性極限范圍內安全工作，因此，要分析解決這些失效形式，才能保證鉸鏈安全工作。

3.1 塑性變形破壞

柔性鉸鏈只有在合理的彈性變形范圍內才能滿足實際應用，失效分析的目的是保證鉸鏈能夠正常安全工作。因此，在本節中考慮了鉸鏈的應力極限和變形范圍。眾所周知，如果鉸鏈的總應力高于材料的屈服強度，則鉸鏈失效形式為塑性變形破壞。因此，在大位移、大載荷范圍內選擇合適的材料是考慮的關鍵問題。

為了對這一問題進行深入分析，筆者比較了結構鋼、不銹鋼和超硬鋁3種材料制成的柔性鉸鏈的性能。采用有限元分析的方法，先建立了三維模型，然后利用Ansys workbench軟件進行了有限元分析，對網格進行劃分；分析采用了非線性條件，以保證收斂結果。表2給出了仿真中每種材料的力學性能，每種材料的失效分析旨在確定鉸鏈的最大載荷、最大應力極限和最大位移。在所有情況下，都考慮了等效應力。沿x軸設置了邊界條件和荷載F，如圖4所示。

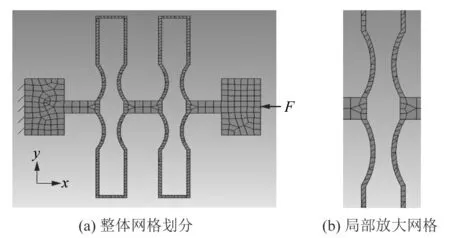
圖4 TLET柔性鉸鏈的網格模型Figure 4 Grid model of TLET flexure hinge

如表2所示，當柔性鉸鏈材料為結構鋼時，可沿x軸承受24 N的最大載荷，在該載荷作用下，柔性鉸鏈沿著x軸的最大位移為4.66 mm，此時最大應力為243.68 MPa，比結構鋼的屈服強度(250 MPa)小。當采用不銹鋼材料時，柔性鉸鏈可承受20 N的最大載荷，沿x軸方向的最大位移為4.03 mm，最大應力為203.07 MPa，比不銹鋼的屈服強度(206 MPa)小。

結果以“平均值±標準差”表示，數據處理與分析采用SPSS 16.0統計軟件進行方差分析和差異顯著性比較，以P＜0.05作為差異顯著性判斷標準。

表2 不同材料TLET柔性鉸鏈的失效分析

結果表明：上述材料保證了柔性鉸鏈可靠、安全的工作條件。盡管柔性鉸鏈允許大的工作行程，但只能承受24 N的最大載荷。筆者考慮了承載力大和工作行程大的特性，決定采用超硬鋁作為柔性鉸鏈的替代材料。

用超硬鋁制造的柔性鉸鏈在自由端施加40 N的載荷時，沿x軸方向可產生21.68 mm的位移，由此產生的最大應力為406.13 MPa。遠比超硬鋁的屈服強度(503 MPa)小。說明了柔性鉸鏈可以安全工作，不會發生塑性變形失效。當載荷增加到50 N時，可沿x軸方向移動27.1 mm，但產生的最大應力為507.67 MPa，大于材料的屈服強度。說明在50 N及以上載荷下，柔性鉸鏈無法保證可靠性。因此超硬鋁制成的柔性鉸鏈的最大載荷應取40 N。

3.2 屈曲性能分析

本節分析前2種屈曲模態。第1種模態：在載荷F的作用下，柔性鉸鏈沿x軸方向被壓縮而產生位移。第2種模態：在載荷F的作用下，柔性鉸鏈沿著z軸方向發生平面外的位移。對這2種模態進行分析，以得到其倍增載荷因子。在所有的屈曲模態中，前2個倍增載荷因子最小。因此，筆者考慮前2個屈曲性能模態來確定前2個倍增荷載因子。對于懸臂梁，可以確定臨界屈曲荷載Pc[15]為

式中：E是彈性模量，I是面積的二階矩，l是鉸鏈長度。

此外，臨界屈曲荷載方程可簡化為

Pc=λ×PI。

式中：λ為倍增載荷因子，PI是初始屈曲載荷。

通過重復使用表2中每種材料的最大載荷值，TLET鉸鏈可能會受到屈曲性能的影響。利用有限元分析，對不同材料的TLET鉸鏈的倍增載荷因子λ進行了分析。表3結果表明，采用超硬鋁材料制成的柔性鉸鏈的倍增載荷因子低于結構鋼和不銹鋼，說明采用超硬鋁材料穩定性較好。

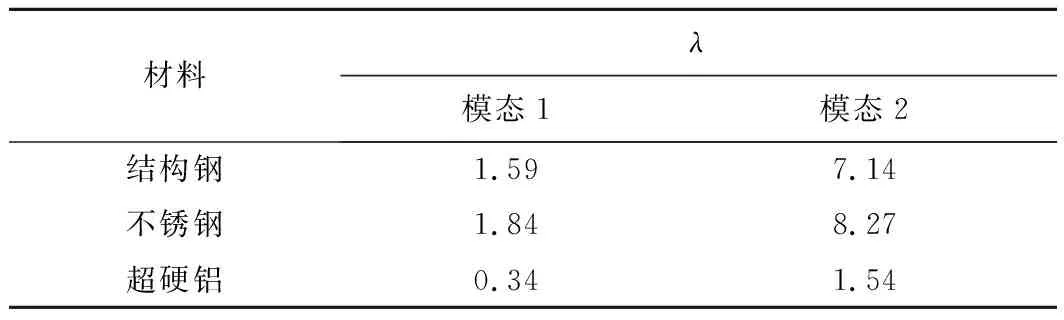
表3 不同材料屈曲性能的結果

4 TLET柔性鉸鏈與LET柔性鉸鏈的性能比較

為了分析TLET鉸鏈的大行程、高承載力的突出性能，將其與傳統的LET鉸鏈進行比較。圖5為傳統LET鉸鏈的二維模型，長度為60 mm、寬度為150 mm，尺寸參數和TLET鉸鏈相等。

圖5 傳統LET柔性鉸鏈的二維模型Figure 5 Two-dimensional model of a traditional LET flexure hinge

圖6表明TLET柔性鉸鏈的位移比傳統鉸鏈的位移大，并且是傳統LET鉸鏈位移的1.8倍，說明所設計的柔性鉸鏈行程性能優于傳統柔性鉸鏈。如果減小傳統柔性鉸鏈的厚度其輸出位移將會得到改善，但由于新型柔性鉸鏈是由2個柔性鉸鏈組成的陣列，因此其輸出位移相對更好。

圖6 LET鉸鏈和TLET鉸鏈的力-位移比較Figure 6 Force-displacement comparison of LET and TLET hinges

考慮到屈曲變形現象，我們分析了二者倍增載荷因子的大小。由圖7可以得到新型鉸鏈的倍增載荷因子比傳統鉸鏈低，說明TLET鉸鏈的穩定性比傳統鉸鏈好。

圖7 LET鉸鏈和TLET鉸鏈的力-倍增載荷因子比較Figure 7 Comparison of force-multiplier load factors for LET and TLET hinges

當TLET鉸鏈沿x軸方向承受壓縮載荷時，TLET不僅沿x軸方向移動，也沿z軸方向移動。這意味著x軸方向上的位移點對應于z軸上的位移點。因此，可以得出TLET鉸鏈沿x軸的輸入位移和沿z軸的輸出位移之間的關系，如圖8所示。

結果表明：TLET鉸鏈沿x軸的輸出位移范圍為2.41～21.68 mm，沿著z軸的輸出位移范圍為5.00～25.12 mm。綜上所述，TLET型柔性鉸鏈沿x軸可實現21.68 mm的大工作行程，沿z軸可實現25.12 mm的大工作行程，TLET鉸鏈的性能遠大于傳統的LET鉸鏈。對于要求變形量大、承載能力強的工作場合，建議采用TLET型柔性鉸鏈。

圖8 TLET柔性鉸鏈沿x軸和沿z軸位移的關系Figure 8 Diagram of displacement of TLET flexure hinge along x axis and z axis

5 結語

1) 課題組提出了一種新型柔性鉸鏈，通過將2個LET柔性鉸鏈以串并聯的方式重新配置，使其能夠實現大行程，高承載能力和安全工作狀態而不發生失效。

2) 課題組推導了TLET柔性鉸鏈等效剛度的解析模型，驗證了不同材料下鉸鏈的塑性變形，最大應力和屈曲失穩行為。

3) 由于TLET鉸鏈僅在特定材料的彈性極限下工作，因此課題組對其失效形式進行了分析。課題組對結構鋼、不銹鋼和超硬鋁等幾種常用材料進行了研究和比較，分析了每種情況下的塑性變形破壞和屈曲變形，選用了超硬鋁作為鉸鏈的材料。

4) 課題組運用有限元法進行分析仿真，結果表明，當載荷作用于TLET型鉸鏈的自由端時，沿著x軸的最大輸入位移為21.68 mm，沿著z軸可獲得超過25.12 mm的位移。并且能夠承受高達40 N的載荷而不發生失效。與傳統LET鉸鏈相比，該鉸鏈的位移是傳統鉸鏈的1.8倍。因此文中所設計的鉸鏈可用于工作行程大，負載能力大的機械裝備中。