二次域中類數h(k)=1時丟番圖方程整數解探討
2021-03-08 06:44:40王振謝清
卷宗 2021年3期
關鍵詞:矛盾
王 振 謝 清
(安徽文達信息工程學院,安徽 合肥 230039)

定理1.1[1]:設K為一個二次域,則必有對于K的代數整數環(huán) kO 有:當
當時,
定理1.2[3]:設K是代數數域,OK為K的代數整數環(huán),且類數為h(k),則:
定理1.3[1]:設M滿足唯一分解整環(huán),從而對于整數k≥2以及α,β∈M(α,β)=1,當αβ=γk.k∈M時,必有:
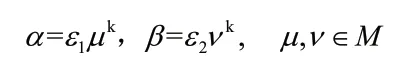
其中ε1,ε2兩個元素是M中的單位元素,而且ε1ε2=εk。
1 主要結論證明
證明方程1

無整數解。
分解(1.1)式可知:
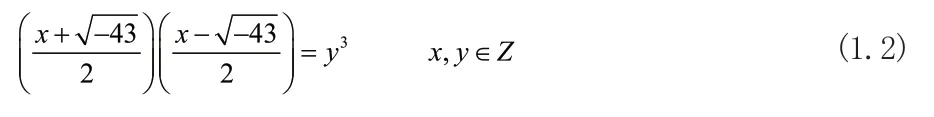
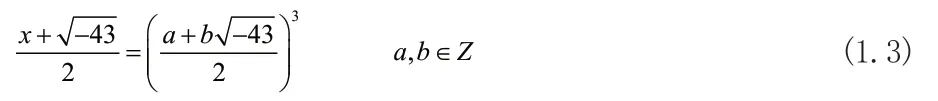
整理等式(1.3)可得:
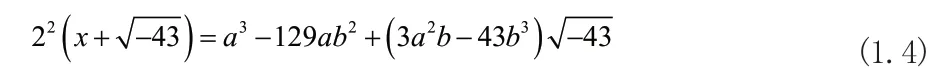
由等式性質比較兩邊系數易知:

若b=±1,代入2.6式得,與矛盾。
若b=±2 , ± 22由于a≡b(mod 2)同奇同偶,從而由等式(1.6)式得:
綜合以上證明可知方程(1.1)無整數解。
證明方程2

無整數解。
分解(1.7)式可知:
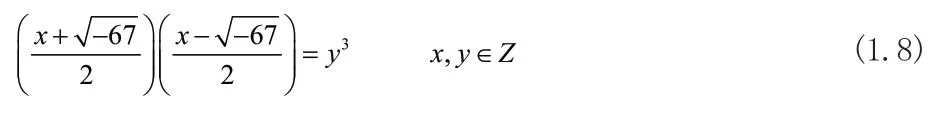
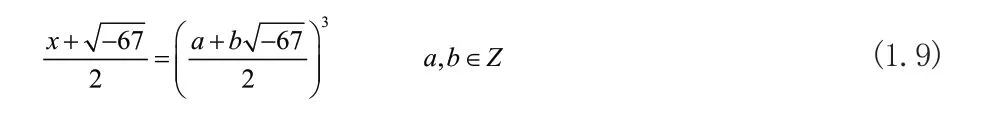
整理等式(1.9)可得:
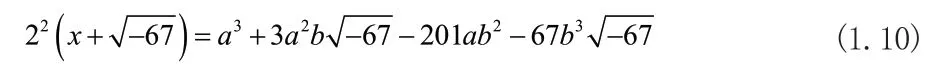
由等式性質比較兩邊系數易知

由等式(1.12)式知:b=±1 ,±2 ,± 22
若b=±1 ,代入(1.12)式可得3a2= 63或71,顯然a?Z與a Z∈ 矛盾。
若b=±2 , ± 22由于a≡b(mod 2)同奇同偶,從而由1.12式得:
左邊22≡22(mod 23)右邊b(3a2-67b2)≡0 (mod 23) 矛盾
從而丟番圖方程(1.7)式無整數解。
猜你喜歡
科學大眾·小諾貝爾(低幼)(2025年4期)2025-04-18 00:00:00
數學雜志(2022年4期)2022-09-27 02:42:48
當代陜西(2021年22期)2022-01-19 05:32:32
中老年保健(2021年2期)2021-08-22 07:29:58
小學生作文(低年級適用)(2020年6期)2020-07-24 08:36:20
作文評點報·低幼版(2020年30期)2020-07-23 06:46:17
童話世界(2020年13期)2020-06-15 11:54:50
讀友·少年文學(清雅版)(2019年4期)2019-08-27 00:46:48
人大建設(2018年5期)2018-08-16 07:09:06
商周刊(2017年11期)2017-06-13 07:32:30

